XY is a line parallel to side BC of a triangle ABC. If BE ∣∣ ACand CF ∣∣ ABmeet XY at E and F respectively, show that ar (ABE) = ar (ACF)
Since, BE||AC⇒BE||YC...(1)
and BC∣∣EY (given)...(2)
∴□BCYE is a parallelogram (∴ pairs of opposite sides are parallel)
Now, since ΔABE and parallelogram BCYE are on the same
base EB and between the same parallels EB and AC,
∴ar(ΔABE)=12ar(∣∣gmBCYE)...(3)
Also, since CF||AB⇒CF||BX
and BC∣∣XF (given)
∴□BCFX is a paralleogram (∴ pairs of opposite sides are parallel)
Now, since ΔACF and parallelogram BCFX are on the same base CF and between the same parallels CF and AB,
∴ar(ΔACF)=12ar(∣∣gmBCFX)....(4)
But ar(∣∣gmBCYE)=ar(∣∣gmBCFX)...(5)
(∴ parallelograms are on the same base BC and between same parallels BC and EF)
∴ From (3), (4) and (5), we have
ar(ΔABE)=ar(ΔACF)

Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar12videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise34videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
XY isa line parallel to side BC of ABC.BEA and CFAB meet XY in E and F respectively.Show that ar(ABE)=ar(ACF).
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
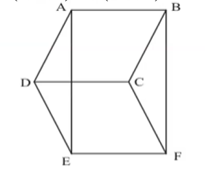
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
 View Solution
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
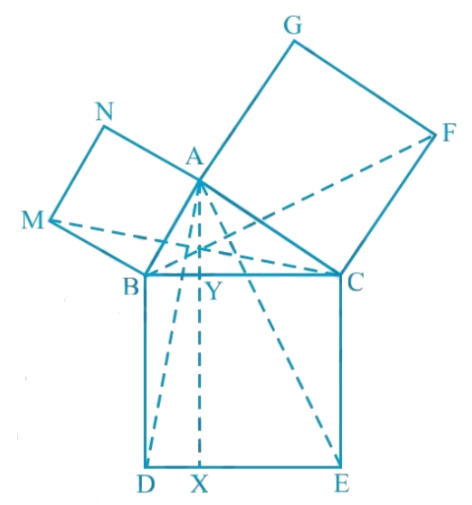
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)= ar (ACFG)
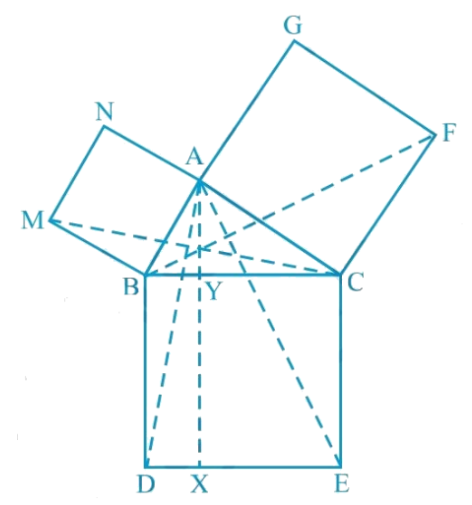 View Solution
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
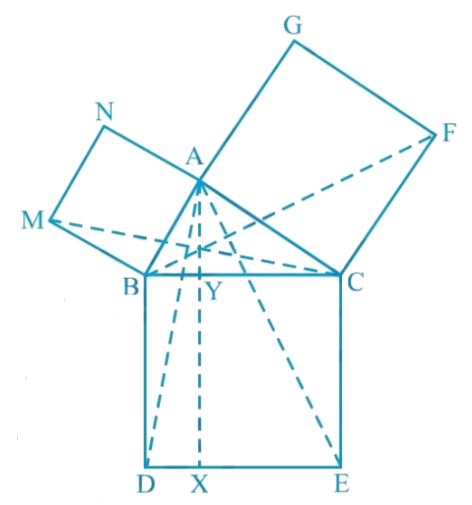 View Solution
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)=2ar( FCB)
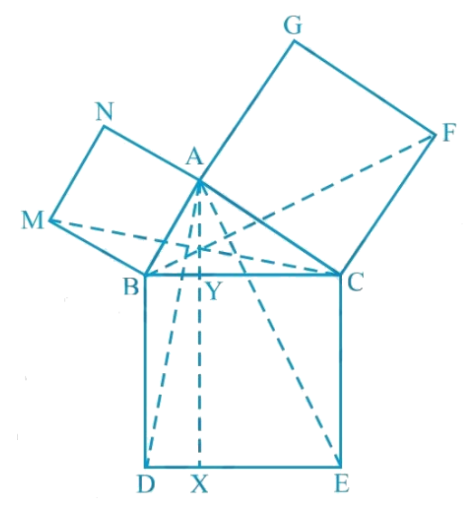 View Solution
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
 View Solution
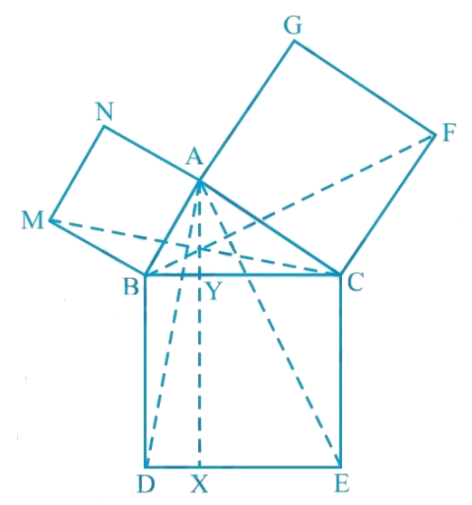
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=ar (ABMN)
 View Solution
View Solution

