One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which an be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.
Let x cakes of first type and y cakes of second type be made.

According to the problem maximise Z=x+y, and constraints x≥0
y≥0
200x+100y≤5000⇒2x+y≤50
25x+50y≤1000⇒x+2y≤40
First draw the graph of the straight lines 2x+y=50 and x+2y=40.

Now find the feasible region using constraints 2x+y≤50,x+2y≤40,x≥0,y≥0 and shade it. The vertices of this shaded region are A(25,0),B(20,10) and C(0,20). We find the value of Z at these vertices.
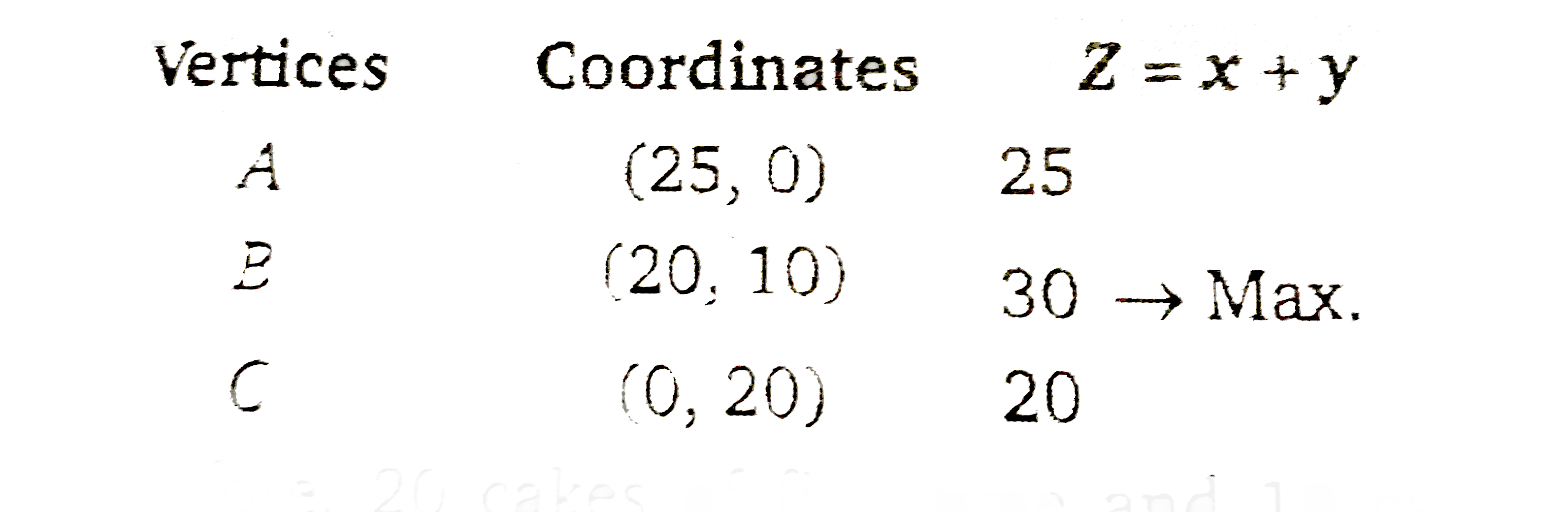
Therefore 20 cakes of first types and 10 cakes fo second types are made.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise9videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.110videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )9videos
INVERES TRIGONOMETRIC FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice15videos
MATRICES
Similar Questions
One kind of cake requires 200 g of flour and 25 g of fat, another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat, assuming that there is no shortage of the other ingredients used in making the cakes. Make it an LPP and solve it graphically.
View Solution(i) One kind of cake requires 200 g of flour and 25 g of fat and another kind of cake requires 100 g of flour and 50 g of fat.Find the maximum number of cakes which can be made form 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.From a linear programming problem and solve it graphically.
(ii) One kind of cake requires 300 g of flour and 15 g of fat, another kind of cake requires 150 g of flour and 30 g of fat.Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 g of fat assuming that there is no shortage of the other ingredients used in making the cakes. Make it as an LPP and solve it graphically.View SolutionOne kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other integredients used in making the cakes. Formulate the above as a linear programming problem and solve graphically.
View SolutionOne kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes that can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.
View SolutionOne kind of cake requires 200g of flour and 25g of fat and another kind of cake requires 100 g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.
View SolutionOne kind of cake requires 200g of flour and 25g of fat and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1kg of fat assuming that there is no shortage of other ingredients used in making the cakes.
View SolutionOne kind of cake requires 300g of flour and 15g of fat, another kind of cake requires 150g of flour and 30g of fat. Find the maximum number of cakes which can be made from 7.5 kg of flour and 600f of fat, assuming that there is no shortage of the other ingredients used in making the cakes. Make it as an L.PP. and solve it graphically.
View SolutionShruti uses 10518g of flour for making 12kg of halwa. How much halwa can she make from 31538g of wheat flour?
View SolutionIce cubes at 0∘C each of mass 200 g are dropped one after the other into 2 kg water at 30∘C in such a awayy that after the first one melts completely, the second one is dropped. If the heat energy required to melt 1 g of ice is 80 cal, determine the maximum number of ice ice cubes that can be dropped into the water such that no ice is left in the water without melting.
View SolutionIce cubes at 0∘C each of mass 200 g are dropped one after the other into 2 kg water at 30∘C in such a awayy that after the first one melts completely, the second one is dropped. If the heat energy required to melt 1 g of ice is 80 cal, determine the maximum number of ice ice cubes that can be dropped into the water such that no ice is left in the water without melting.
View Solution

