A diet is to contain at leat 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 cost Rs. 4 per unit and F2 costs Rs. 6 per unit. One unit of food F1 contains 3 uinits of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
Let x units of F1 and y units of F2 be in the food. Then,

Maximise Z=4x+6y…………….1
Constraints 3x+6y≥80 ………………….2
4x+3y≥100……………….3
x≥0,y≥0…………………..4
First, draw the graph of the line 3x+6y=80,.
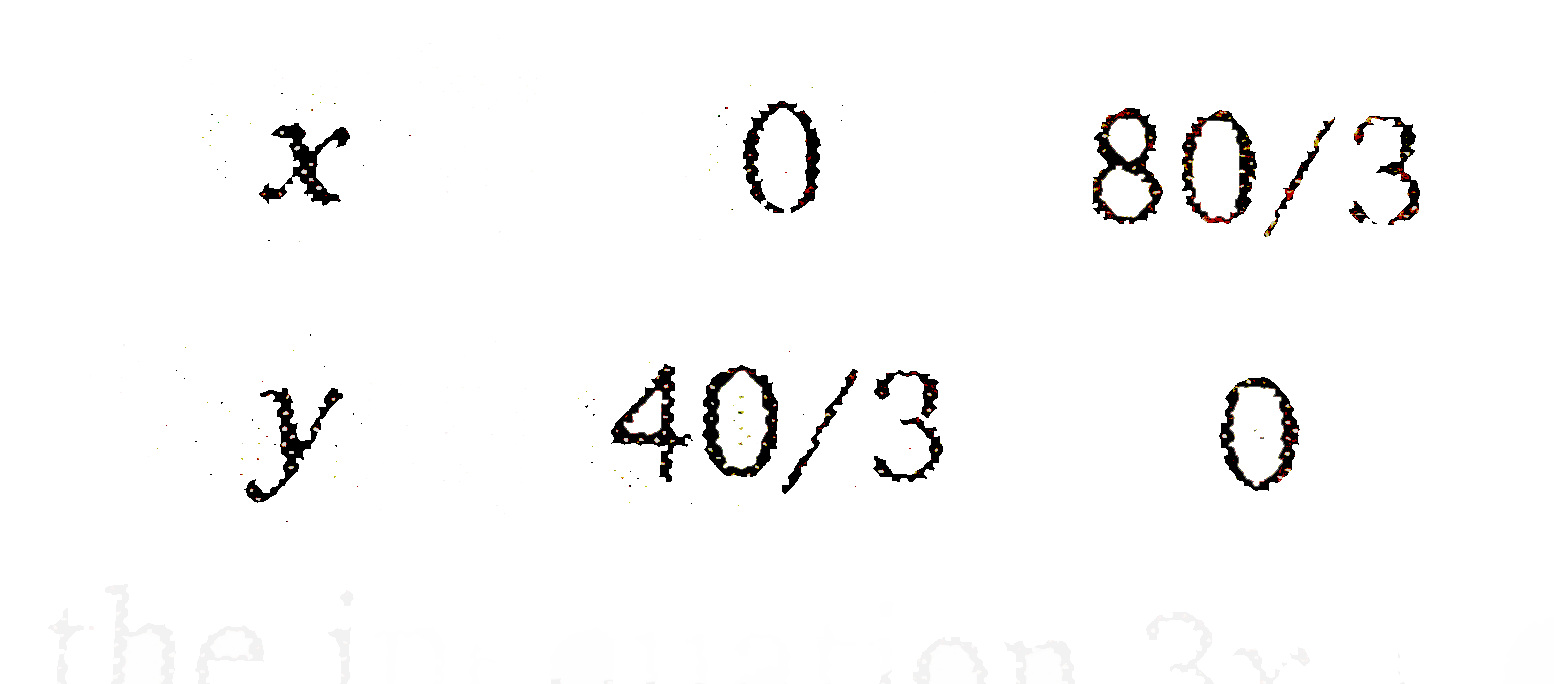
Put (0,0) in the inequation 3x+6y≥80,
3×0+6×0≥80⇒0≥80 (False)
Thus, the half plane does not contain the origin.
Since x,y≥0 so the feasible solution is in the first quadrant.
Now, draw the graph of the line 4x+3y=100

Put (0,0) in the inequation 4x+3y≥100,
4×0+3×0≥100
⇒0≥100 (False)
Thus, the half plane does not contain the origin.
From equations 3x+6y=80 and 4x+3y=100. The point of intersection is B(24,43)
Clearly, the feasible region is unbounded.
The vertices the feasible region are A(803,0),B(24,43) and C(0,1003). We find the value of Z at these vertices.
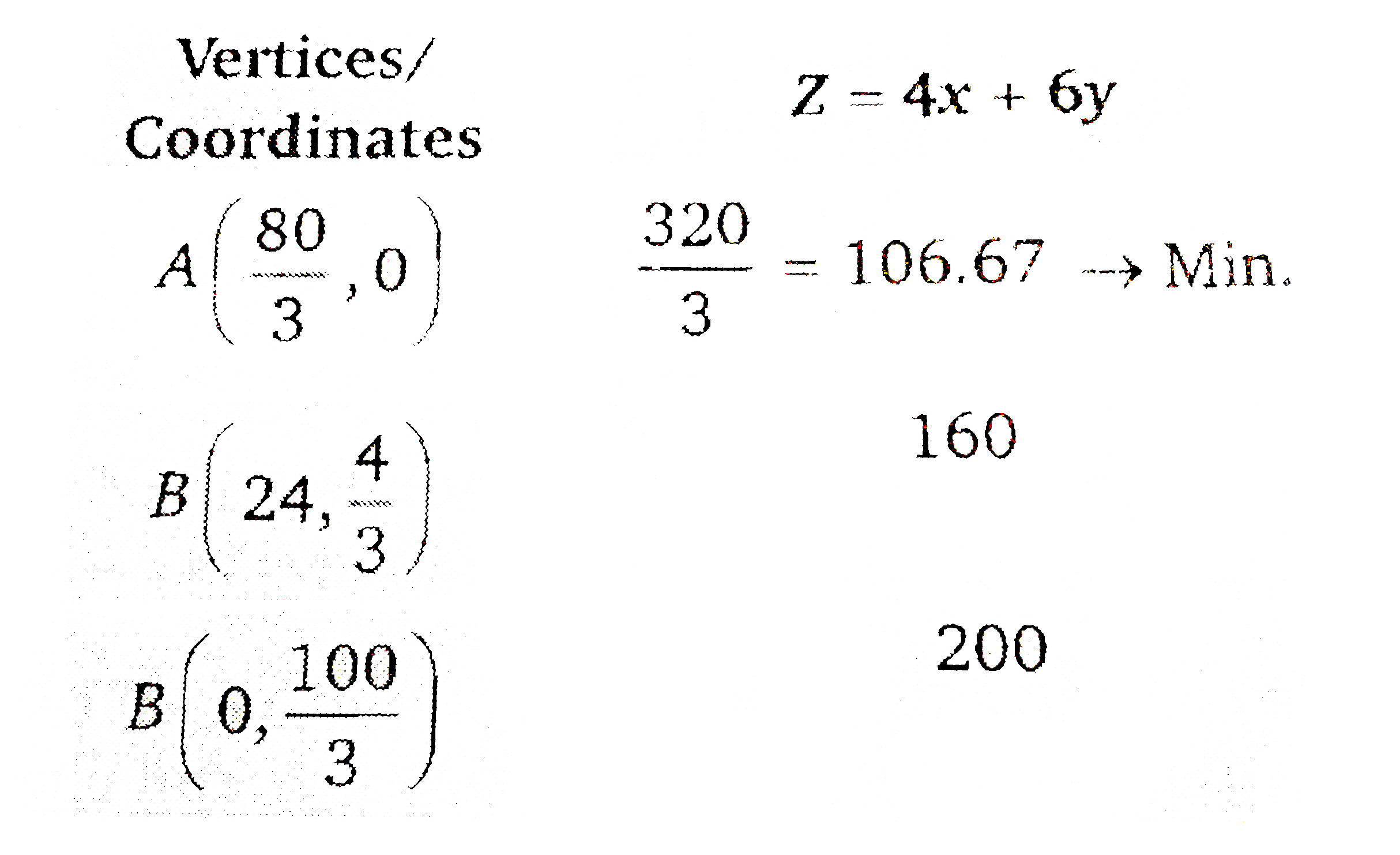
Since the feasible region is unbounded, so the minimum value of z may or may not be 104. For this we draw the graph of inequations 4x+6t<104 or 2x+3y<52. There is no common point here, so the minimum cost of mixture is Rs. 104.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise
9 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.1
10 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
(Diet problem) A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calciums atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum amount of vitamin A? How many packets of each food should be used to maximise the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?
View SolutionMaximise Z=3x+4y
Subject to the constraints
x+y≤4,x≥0,y≥0
View SolutionProve that:tan−1√x=12cos−1(1−x1+x),x∈[0,1]
View SolutionLet A=[0100]show that (aI+bA)n=anI+nan−1bA, where I is the identitymatrix of order 2 and n∈N.
View SolutionA diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2, are available. Food F1costs Rs 4 per unit food and F, costs Rs 6 per unit. One unit of food F1, contains 3 units of vitamin A and 4 units of minerals.One unit of foodF2,contains 6 units of vitamin A and 3 units of minerals.Formulate a LPP. find the minimum cost of diet which matches the minimal requirement
View Solutionएक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन 4 और 100 मात्रक स्रनिज होना चाहिए। दो प्रकार के भोज्य F1 और F2 उपलब्ध हैं। भोज्य F1 की लागत Rs 4 प्रति नात्रक और F2 की लागत Rs 5 प्रति मात्रक है। भोज्य F की एक इकाई में कम से कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है। F2 की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज हैं। इसको एक रखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए। उस आहार का न्यूजतम मूल्य ज्ञात कीजिए, जिसमें इन दो भोज्यों का मिश्रण है और उसें न्यूनतम पोषक तत्तव हैं।
View SolutionA diet of a sick person must contains at least 48 units of vitamin A and 64 units of vitamin B. Two foods F1andF2 are available. Food F1 costs Rs. 6 per unit and Food F2 costs Rs. 10 per unit. One unit of food F1 contains 6 units of vitamin A and 7 units of vitamin B. One unit of food F2 contains 8 units of vitamin A and 12 units of vitamin B. Find the minimum cost for the diet that consists of mixture of these two foods and also meeting the minimum nutritional requirements.
View Solutionएक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए । दो प्रकार के भोज्य F1 और F2 उपलब्ध हैं । भोज्य F1 की लागत Rs 4 प्रति मात्रक और Rs F2 की लागत Rs 5 प्रति मात्रक है । भोज्य F1 की एक इकाई में कम से कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है । F2 की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज हैं । इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए । उस आहार के न्यूनतम मूल्य ज्ञात कीजिए, जिसमे इन दो भोज्यों का मिश्रण है और उसमे न्यूनतम पोषक तत्व हैं ।
View Solutionएक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य F1 और F2 उपलब्ध हैं। भोज्य F1 की लागत 4 रू0 प्रति मात्रक और F2 की लागत 5 रू0 प्रति मात्रक है। भोज्य F1 की एक इकाई में कम से कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है। F2 की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज है। हम उस आहार का न्यूनतम मूल्य ज्ञात करना चाहते हैं। जिसमें इन दो भोजयों का मिश्रण है और उसमें न्यूनतम पोषक तत्व हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप मे सूत्रबद्ध कीजिए ताकि आहार का मूल्य न्यूनतम हो।
View Solutionएक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य F1 और F2 उपलब्ध हैं। भोज्य F1 की लागत Rs. 4 प्रति मात्रक और F2 की लागत Rs. 5 प्रति मात्रक है। भोज्य F1 की एक इकाई में कम से कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है। F2 की प्रति इकाई कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए। उस आहार का न्यूनतम मूल्य ज्ञात कीजिए, जिसमें इन दो भोज्यों का मिश्रण है और उसमें न्यूनतम पोषक तत्व हैं।
View SolutionDiet of a sick person must contains at least 4000 units of vitamins, 50 units of minerals and 2500 calories. Two foods F1andF2 cost Rs. 50 and Rs. 75 per unit respectively. Each unit of food F1 contains 200 units of vitamins, 2 units of minerals and 40 calories,F_(2) contains 100 units of vitamins, 3 units of minerals and 35 calories. Formulate the above problem as LPP to fulfil sick person's requirements at minimum cos.
View SolutionA diet of sick person contains at least 48 units of vitamin A and 64 uints of vitamin B. Two foods F1andF2 are available . Food F1 costs Rs. 6 per unit and food F2 costs Rs. 10 per unit. One unit of food F1 contains 6 units of vitamin A and 7 units of vitamin B. One unit of of food F2 contain 8 units of vitamin A and 12 units of vitamin B. Formulate the LPP, for the minimum cost for the diet that consists of mixture of these two foods and also meeting the minimal nutrition requirements
View Solutionएक भोज्य पदार्थ में कम-से-कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए | दो प्रकार के भोज्य F1और F2उपलब्ध है | भोज्य F1की लागत ₹ 4 प्रति मात्रक और F2 लागत ₹ 5 प्रति मात्रक है | भोज्य F1की एक इकाई में कम-से-कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है | F2 की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज है | इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबध्द कीजिए | उस आहार का न्यूनतम मूल्य ज्ञात कीजिए जिमसें इन दो भोज्यों का मिश्रण है और उसमें न्यूनतम पोषक तत्व है |
View Solutionएक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन 4 और 100 मात्रक स्रनिज होना चाहिए। दो प्रकार के भोज्य F1 और F2 उपलब्ध हैं। भोज्य F1 की लागत Rs 4 प्रति नात्रक और F2 की लागत Rs 5 प्रति मात्रक है। भोज्य F की एक इकाई में कम से कम 3 मात्रक विटामिन A और 4 मात्रक खनिज है। F2 की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज हैं। इसको एक रखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए। उस आहार का न्यूजतम मूल्य ज्ञात कीजिए, जिसमें इन दो भोज्यों का मिश्रण है और उसें न्यूनतम पोषक तत्तव हैं।
View SolutionA diet is to contain atleast 80 units of vitamin A and 100 units of minerals . Two foods F_(1)" and " F_(2) are available . Food F_(1) costs Rs 4 per unit and food F_(2) costs Rs 6 per unit . One units of food F_(1) contains at 3 units of vitamin A and 4 units of minerals . One unit of food F_(2) contains 6 units of vitamin A and 3 units of minerals . Formulate this as a linear programming problem . find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements .
View Solution
