Obtain an expression for the equivalent emf and internal resistance of two cells connected in parallel.Solution in Kannada

Video Solution

Text Solution

Verified by Experts

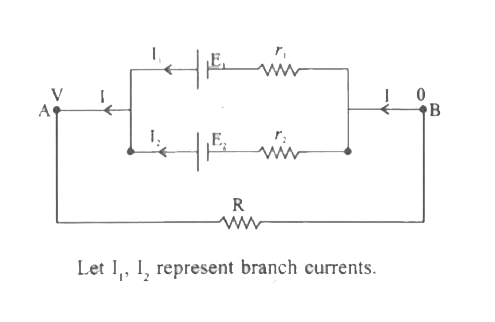
Let $I_{1}, I_{2}$ represent branch currents.
Let V be the common potential , so that ,
$I_{1} = \frac{E_{A} - V}{r_{1}}, I_{2} = \frac{E_{2} - V}{r_{2}}$
hence, $I = \frac{E_{1} - V}{r_{1}} + \frac{E_{2} - V}{r_{2}}$
i.e., $I = (\frac{E_{1}}{r_{1}} + \frac{E_{2}}{r_{2}}) - V (\frac{1}{r_{1}} + \frac{1}{r_{2}})$
Comparing this with the terminal potential difference,
$V_{E}_(e q) - I r_{e q}$
i.e., $V = E_{e q} - \frac{1}{(\frac{1}{r_{e q}})}$
For two cells in parallel combination ,
${(E_{e q})}_{p} = \frac{\frac{E_{1}}{r_{1}} + \frac{E_{2}}{r_{2}}}{\frac{1}{r_{1}} + \frac{1}{r_{2}}} = \frac{E_{1} r_{2} + E_{2} r_{1}}{r_{1} + r_{2}}$
$\frac{1}{{(r_{e q})}_{p}} = \frac{1}{r_{1}} + \frac{1}{r_{2}}$ and main current = $i = \frac{E_{e q}}{R + r_{e q}}$
Note : (i) For .n. cells in parallel
$V = ⎡ ⎢ ⎣ \frac{\sum_{r = 1}^{n} \frac{E_{i}}{r_{i}}}{\sum_{i = 1}^{n} \frac{1}{r_{1}}} ⎤ ⎥ ⎦ - ⎡ ⎣ \frac{I}{\sum_{i = 1}^{n} \frac{1}{r_{1}}} ⎤ ⎦$ ,
${(E_{e q})}_{parallel} = ⎡ ⎢ ⎣ \frac{\sum_{r = 1}^{n} \frac{E_{i}}{r_{i}}}{\sum_{i = 1}^{n} \frac{1}{r_{1}}} ⎤ ⎥ ⎦ - ⎡ ⎣ \frac{I}{\sum_{i = 1}^{n} \frac{1}{r_{1}}} ⎤ ⎦$ and ${(\frac{1}{r_{e q}})}_{p} = n \sum i - 1 (\frac{1}{r_{i}})$ .
(ii) For .n. number of identical cells
E-emf of each cell
r-internal resistance of each cell.
${(E_{e q})}_{p} = \frac{n (\frac{E}{r})}{n (\frac{1}{r})}$
i.e., ${(E_{e q})}_{p} = E$
and ${(\frac{1}{r_{e q}})}_{p} = n (\frac{1}{r})$
i.e. ${(r_{e q})}_{p} = \frac{r}{n}$
Main current , $I = \frac{n E}{R + \frac{n}{r}}$ and terminal potential difference across cells V=IR.

|

Updated on:21/07/2023

Class 12 PHYSICS ANNUAL EXAM QUESTION PAPER MARCH 2018

Topper's Solved these Questions

Similar Questions

SUBHASH PUBLICATION-ANNUAL EXAM QUESTION PAPER MARCH 2018-QUESTION

Home
Ask Doubt
Profile