For the damped oscillator shown in previous Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.
(a) km=45×0.4=18kgNm−1=18kg2s−2
∴√km=4.243kgs−1
b=0.08kgs−1 is much less than √km . Hence, the time period T from equation ( 49) is given by
T=2π√mk
=2π√0.445=0.6s
(b) From equation ( 48), the time T1/2 for amplitude to drop to half of its initial value of given by T1/2=log(2)b2m
=0.6920.082×0.4
=6.93s
(c ) For calculateing the time t12 for its mechanical energy to drop to half its initial value we make use of equation (50)
E(t12)/E(0)=exp. ⎛⎜⎝−bt12m⎞⎟⎠
12=exp⎛⎜⎝−bt12m⎞⎟⎠
ln(12)=−bt12m
or t12=0.69280gs−1×400g
=3.46s
This is just half of the decay period for amplitude, which is not surprising, because, according to equations ( 48 ) and ( 50) , energy depends on the square of the amplitude. Notice that there is a factor of 2 in the exponents of the two exponentials.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Exercise20videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)60videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-J )8videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)5videos
PHYSICAL WORLD
Similar Questions
For the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
(a) The period of oscillation
(b) Time taken for its amplitude of vibrations to drop to half of its initial values
(c) The time for the mechanical energy to drop to half initial values
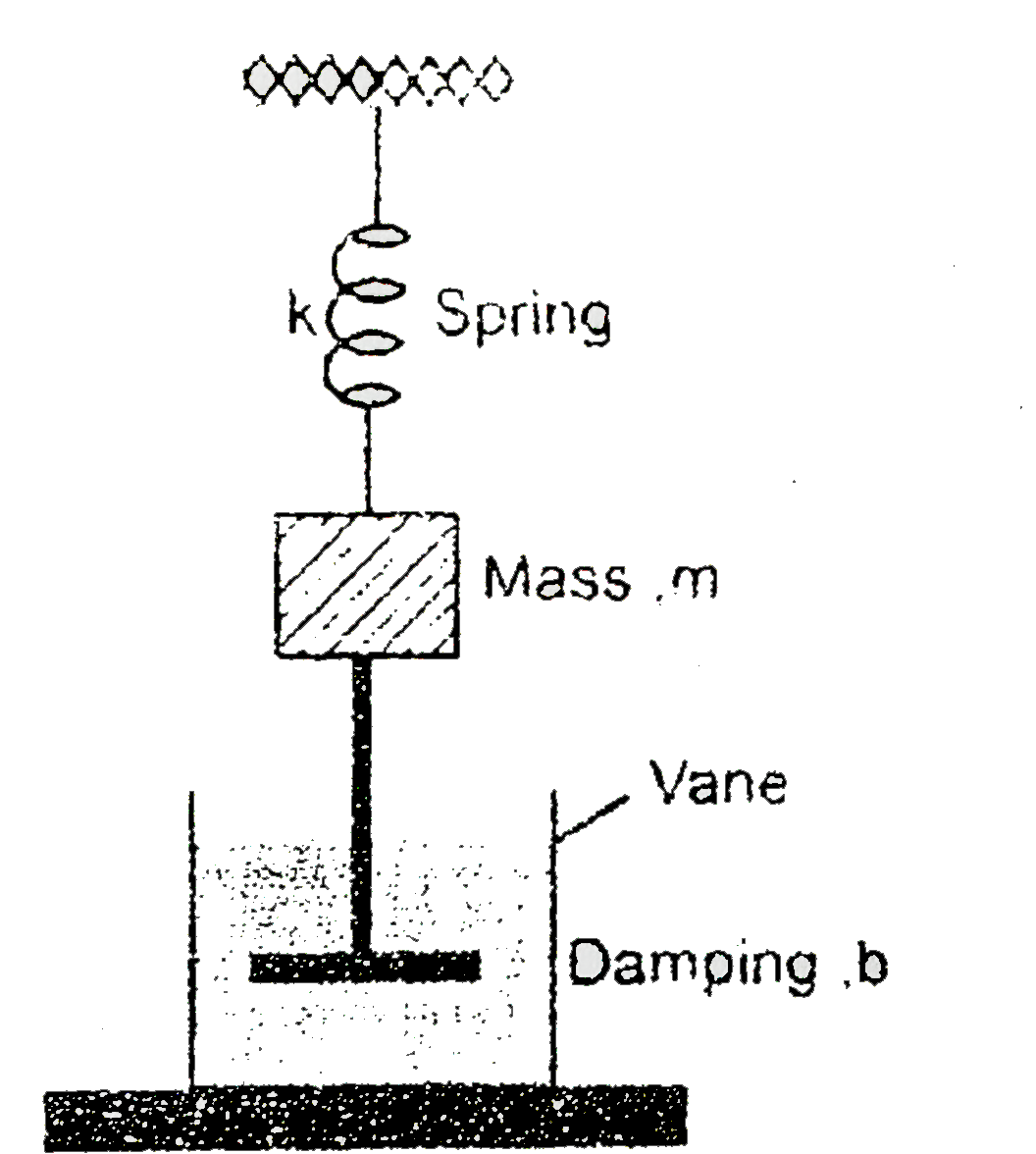 View Solution
View SolutionIn damped oscillatory motion a block of mass 20kg is suspended to a spring of force constant 90N/m in a medium and damping constant is 40g/s. Find (a) time period of oscillation (b) time taken for amplitude of oscillation to drop to half of its intial value (c) time taken for its mechanical energy to drop to half of its initial value.
View Solution
Knowledge Check
- Question 1 - Select One
For a damped oscillator the mass 'm' of the block is 200 g, k = 90 N m−1 and the damping constant b is 40 g s−1. Calculate the period of oscillation.
A0.2B0.3C0.5D0.1 - Question 2 - Select One
In the question number 93, the time elapsed for its mechanical energy to drop half of its initial value is
A2.5 sB3.5 sC4.5 sD7.5 s - Question 3 - Select One
For the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10 g s^(-1) The time period of oscillation is (approx.)
A2πsB2π13sCπ5sDπ√5s
For the damped oscillator shown in previous figure, k=180Nm−1 and the damping constant b is 40gs−1 .Period of oscillation is given as 0.3 s, find the mass of the block . (Assume b is much less than √km).
View SolutionFor the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
How long does it take for the mechanical energy to drop to one-half its initial value?View SolutionFor the damped oscillator shown in previous figure, k=180Nm−1 and the damping constant b is 40gs−1 .Period of oscillation is given as 0.3 s, find the mass of the block . (Assume b is much less than √km).
Hint :T=2π√mkView Solution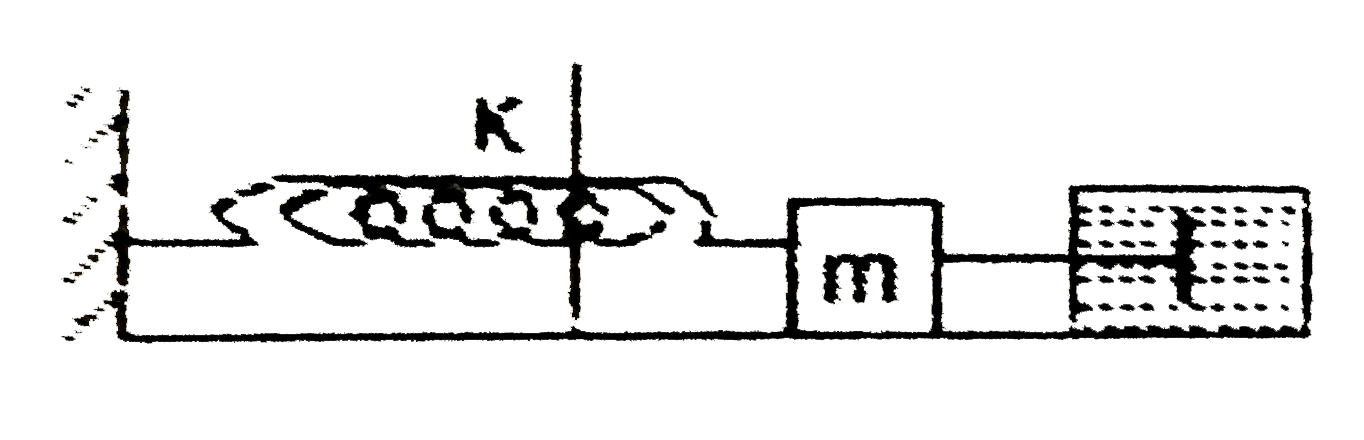
For a damped oscillator which follow the equation →F=−k→x−b→V
the mass of the block is 100 gm K=100N/M and the damping constant is 20 gm/sec. thhen find the time taken for its mechanical energy to drop to one-fourth of its initial value.View SolutionThe displacement of a damped harmonic oscillator is given by x(t)=e−0.1tcos(10πt+ϕ). Here t is in seconds
The time taken for its amplitude of vibration to drop to half of its initial is close to :View Solution

