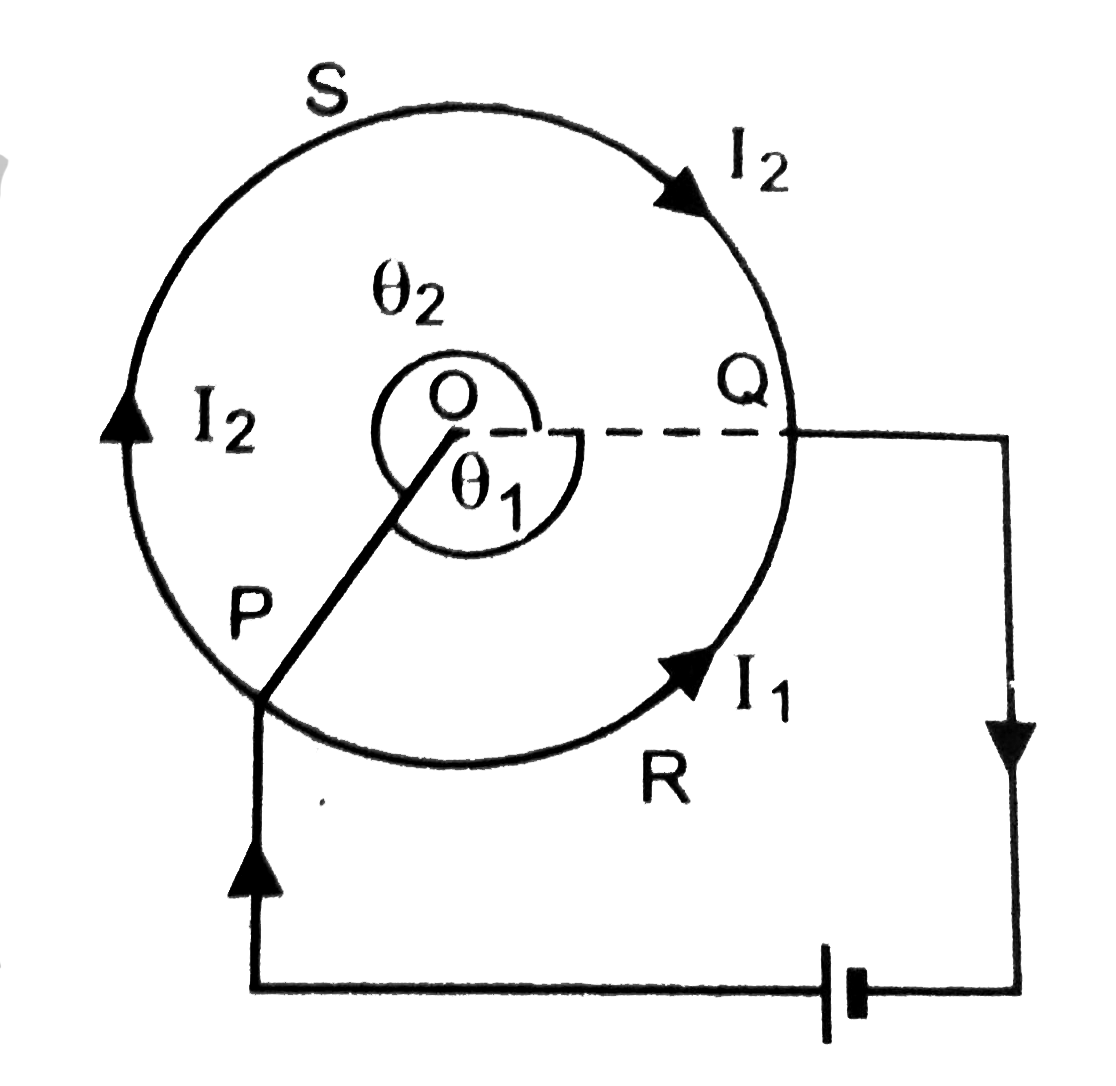
As shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.
Let I1 and I2 be the lengths of the segments of the uniform conductor and R1,R2 their respective resistance.
and i1i2=R2R1=l2l1
So, B1B2=i1l1i2l2
(l2l1)(l1l2)=1
i.e..,B1=B2
But the currents in the two segments are in opposite directions with respect to O. Therefore the magnetic induction →B1 is out of the paper and B, is into the paper. So they are opposite to each other and they cancel each other. Vectorially →B1=−B2.Therefore, B= net magnetic induction B1+B2=0.
Similar Questions
Knowledge Check
- Question 1 - Select One
The magnetic induction at the centre O in the figure shown in
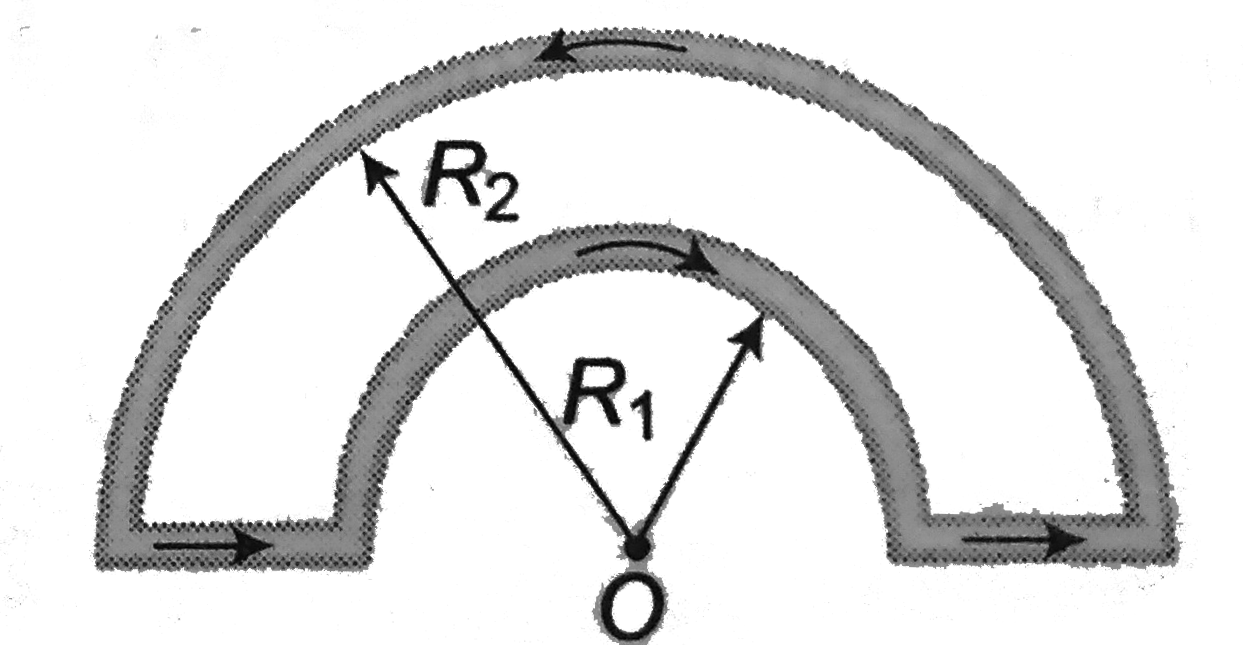 Aμ0i4(1R1−1R2)Bμ0i4(R1+R2)Cμ0i4(R1+R2)Dμ0i4(R1+R2)
Aμ0i4(1R1−1R2)Bμ0i4(R1+R2)Cμ0i4(R1+R2)Dμ0i4(R1+R2) - Question 2 - Select One
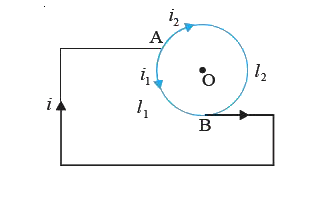
A cell is connected between two points of a uniformly thick circular conductor. The magnetic field at the centre of the loop will be
(Here i1 and i2 are the currents flowing in the two parts of the circular conductor of radius 'a' and μ0 has the usual meaning)AZeroBμ02a(i1−i2)Cμ02a(i1+i2)Dμ0a(i1+i2) - Question 3 - Select One
Current I is flowing in a conductor shaped as shown in the figure. The radius of the curved part is r and the length of straight portion is very large. The value of the magnetic field at the centre will be
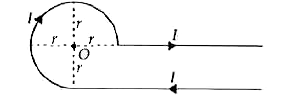 Aμ04πr(π2+1)Bμ04πr(π2−1)Cμ04πr(3π2+1)Dμ04πr(3π2−1)
Aμ04πr(π2+1)Bμ04πr(π2−1)Cμ04πr(3π2+1)Dμ04πr(3π2−1)
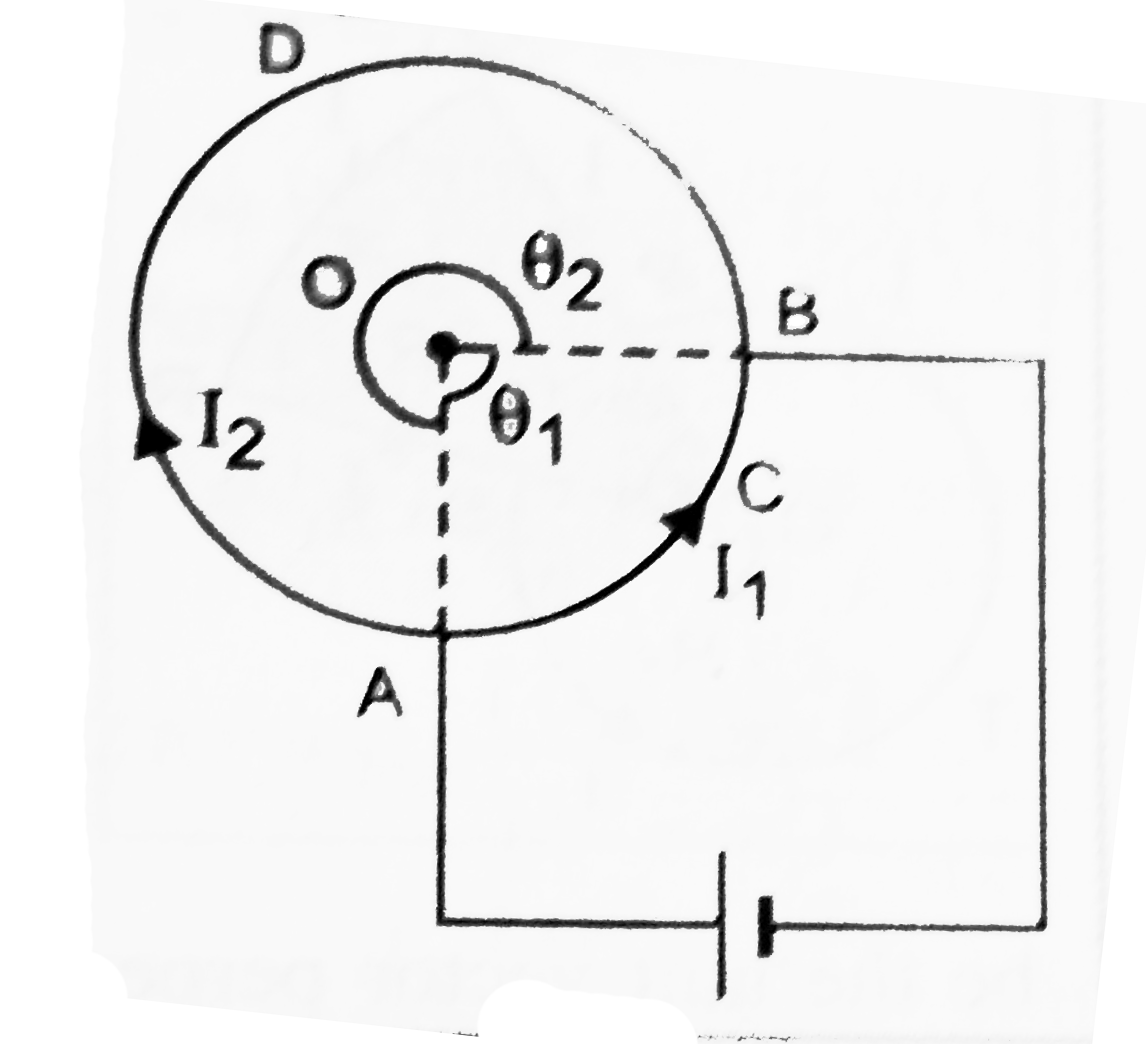
Two long straight conductors are connected radially to two arbitary points A and B of a circular conductor. Calculate the magnetic field at the center of the coil.
 View Solution
View SolutionAs shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.
 View Solution
View SolutionA current I is flowing in a conductor shaped as shown in figure. The radius of the curved part is r and length of straight portion is very large. Find the magnetic field induction at the centre O.
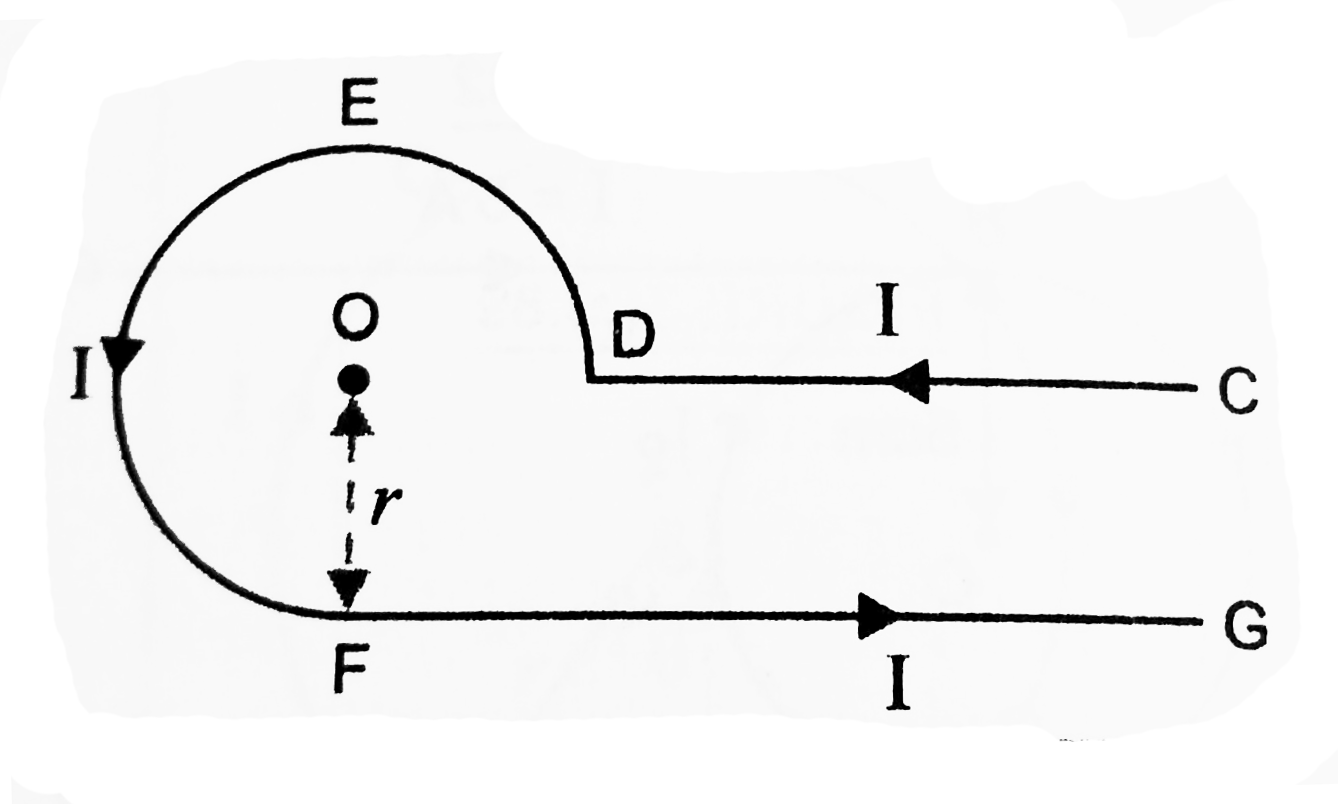 View Solution
View SolutionWhat is the magnetic moment of a current carrying thin circular loop if the radius of the loop is equal to R and the magnetic induction at its centre is equal to B ?
View SolutionA cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
View Solution