D is the mid point of side BC and AE⊥BC. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii)b2+c2=2p2+a22Solution in Tamil
The correct Answer is:b2=p2+ax+a24
Step by step video, text & image solution for D is the mid point of side BC and AE bot BC. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that (i) b^(2)=p^(2)+ax+(a^(2))/(4) (ii) c^(2)=p^(2)-ax+(a^(2))/(4) (iii) b^(2)+c^(2)=2p^(2)+(a^(2))/(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO THINKING CORNER
7 Videos
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO PROGRESS CHECK
21 Videos
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - SOLUTION TO EXERCISE 4.5
15 Videos
- CO-ORDINATE GEOMETRY BOOK - PREMIERS PUBLISHERSCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Other Important Objective
25 Videos
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
16 Videos
Similar Questions
Are square and a rhombus similar or congruent. Discuss.
View SolutionAll circles are …………. (congruent/similar).
View SolutionIf in triangles ABC and EDF, ABDE=BCFD then they will be similar, when
View SolutionThe area of the triangle formed by the points (0,0),(3,0) and (0,4) is :
View SolutionMatch the following:
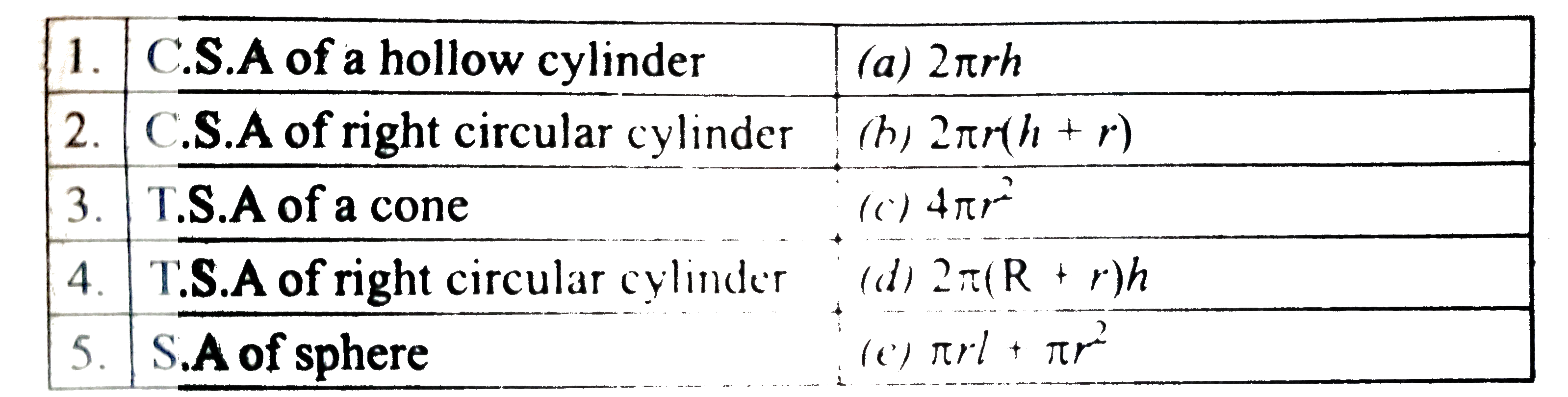
View SolutionProve that identities: ∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣=(ab+bc+ac)3
View SolutionProve |[-bc, b^2+bc, c^2+bc] , [a^2+ac, -ac, c^2+ac] , [a^2+ab, b^2+ab, -ab]|=(ab+bc+ca)^2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCxDE+14BC2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View SolutionIf a, b, c are in A.P., then prove that :
(i)ab+bc=2b2
(ii) (a−c)2=4(b2−ac)
(iii) a2+c2+4ca=2(ab+bc+ca).
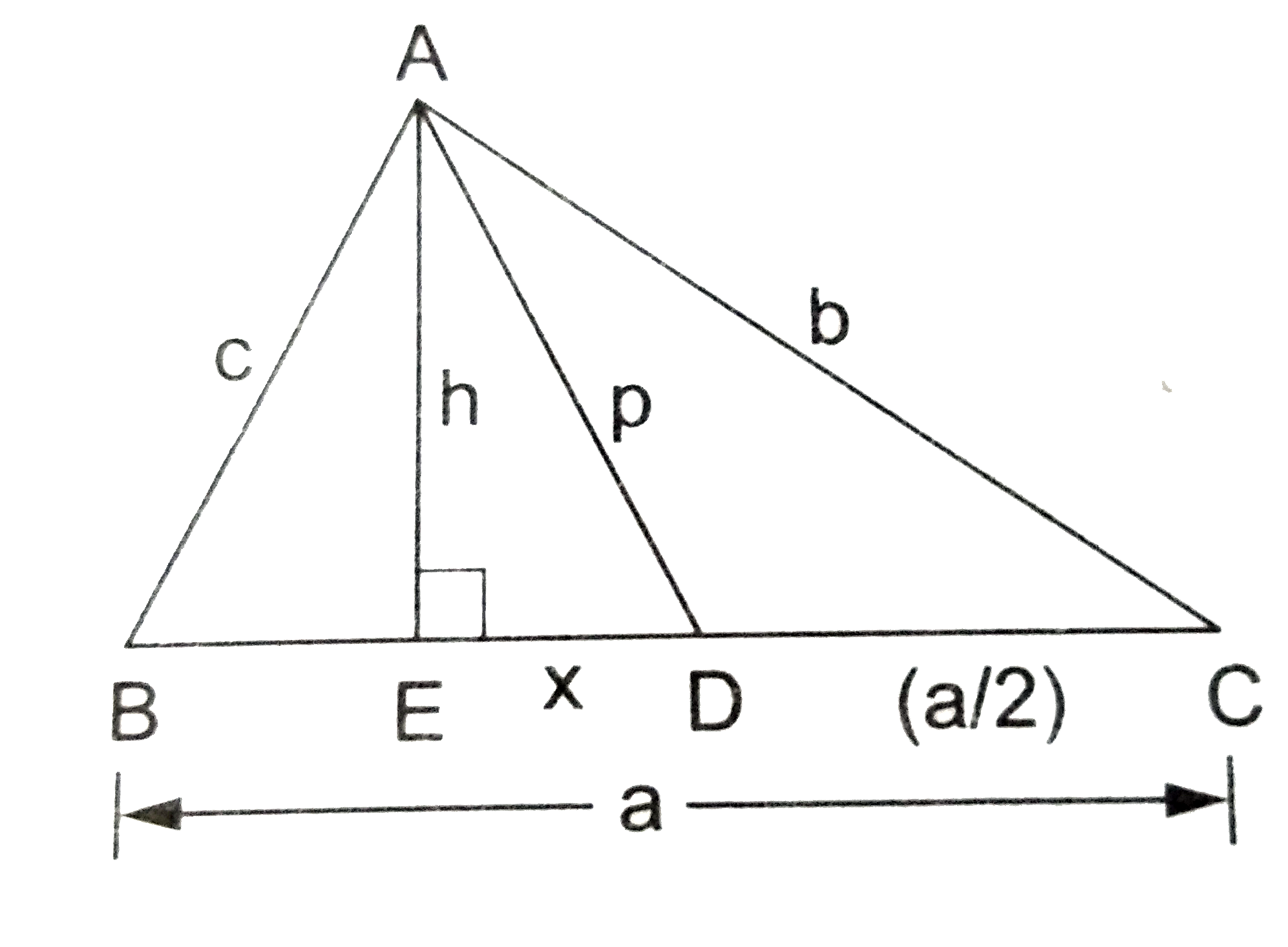
View SolutionIn the given figure, D is the midpoint of side BC and AE⊥BC. If BC=a,AC=b,AB=c,ED=xAD=pandAE=h prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii) (b2+c2)=2p2+12a2
(iv)(b2−c2)=2ax.
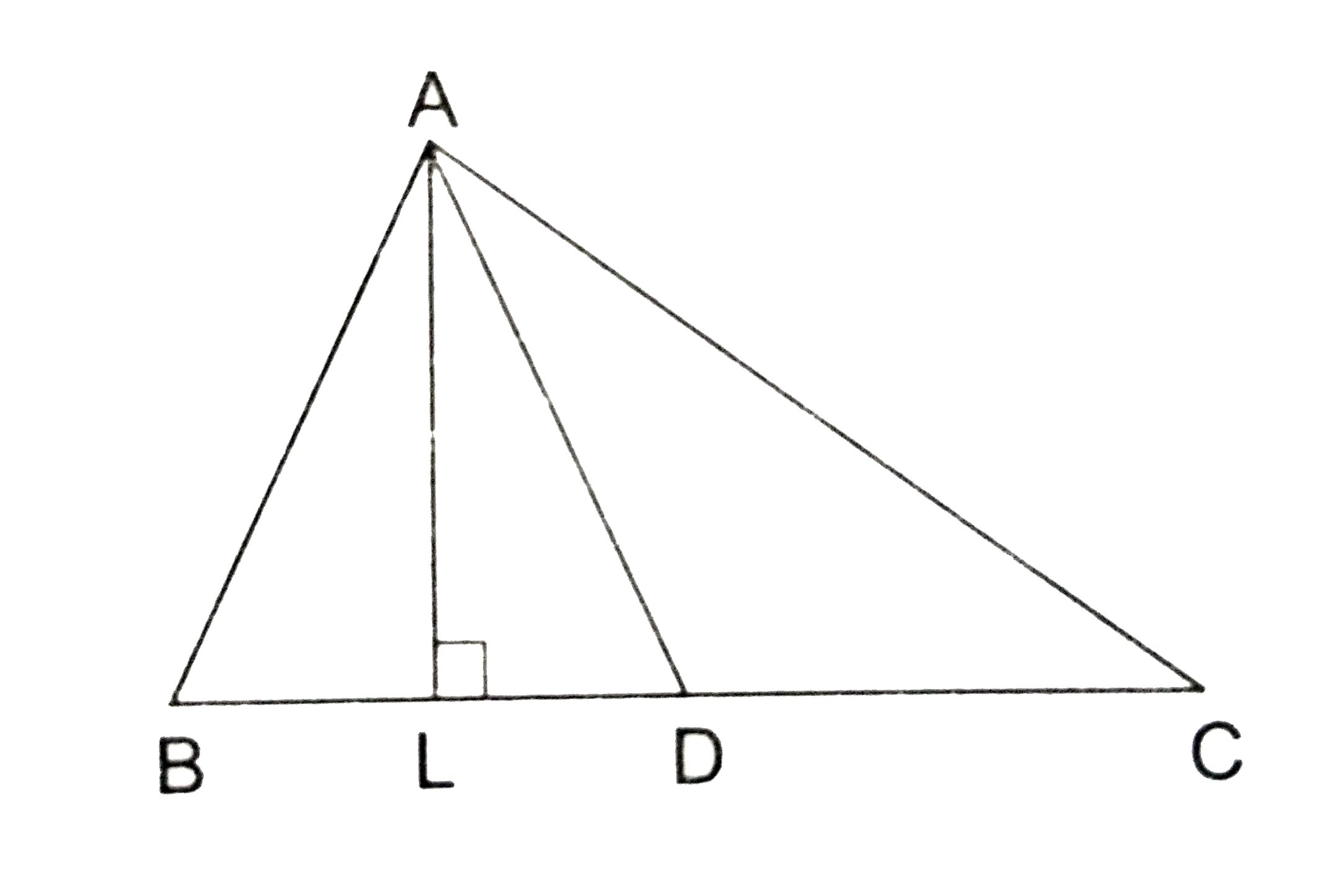
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
View Solutionएक △ABC में, AC>BD है | D, BC का मध्य बिन्दु है तथा AE⊥BC तो सिद्ध कीजिए कि :
(i) AC2=AD2+BC⋅DE+14BC2
(ii) AB2=AD2−BC⋅DE+14BC2
View Solutionत्रिभुज ABC में D भुजा BC का मध्यबिंदु है और AE⊥BC सिद्ध कीजिए कि
(i) AC2=AD2+BC.DE+14BC2
AB2=AD2−BC.DE+14BC2
View SolutionIf BC =a, AC=b, AB=c , AD=p, DE=x so (i) b ^(2) =p^(2) +ax +1/4 a ^(2) (Ii) c^(2) =p^(2)-ax+1/4 a^(2)
View SolutionD is the mid point of side BC and AE⊥BC. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii)b2+c2=2p2+a22
View Solution
