For one mole of a monoatomic gas :-
Column-IColumn-II(A)Isothermal bulk modulus, (p)−RTV2(B)Adiabatic bulk modulus (q)−5P3V(C)Slope of P-V graph in isothermal process (r)T/V(D)Slope of P-V graph in adiabatic process(s)4T/3V(t)None
To solve the problem, we need to match the items in Column I with the correct expressions in Column II for a monoatomic gas. Let's analyze each item step by step.
Step 1: Isothermal Bulk Modulus (A)
The isothermal bulk modulus B is defined as:
B=−dpdV
For an isothermal process, we know that PV=nRT. For one mole of gas, P=RTV.
Differentiating P with respect to V gives:
dp=−RTV2dV
Substituting this into the bulk modulus expression:
B=−−RTV2dVdV=RTV2
Thus, the isothermal bulk modulus is:
B=RTV2
This matches with option (p): −RTV2.
Step 2: Adiabatic Bulk Modulus (B)
The adiabatic bulk modulus Ba is given by:
Ba=−dpdV
For an adiabatic process, we have:
PVγ=constant
For a monoatomic gas, γ=53. Thus:
P=CV5/3
Differentiating gives:
dp=−5C3V8/3dV
Substituting into the bulk modulus expression:
Ba=−−5C3V8/3dVdV=5C3V8/3
Using C=PV5/3 and substituting back gives:
Ba=5P3V
This matches with option (q): −5P3V.
Step 3: Slope of P-V Graph in Isothermal Process (C)
The slope of the P-V graph in an isothermal process is given by:
slope=dpdV
From the earlier derivation, we have:
dp=−RTV2dV
Thus:
dpdV=−RTV2
The slope is negative, and we can express it as:
slope=−RTV2
This matches with option (r): TV.
Step 4: Slope of P-V Graph in Adiabatic Process (D)
For the adiabatic process, the slope is given similarly:
slope=dpdV
From our earlier derivation:
dp=−5P3V8/3dV
Thus:
dpdV=−5P3V8/3
This matches with option (s): 4T3V.
Final Matching
Now we can summarize the matches:
- (A) Isothermal bulk modulus: (p) −RTV2
- (B) Adiabatic bulk modulus: (q) −5P3V
- (C) Slope of P-V graph in isothermal process: (r) TV
- (D) Slope of P-V graph in adiabatic process: (s) 4T3V
Conclusion
The final answer is:
- A → p
- B → q
- C → r
- D → s
The isothermal bulk modulus B is defined as:
B=−dpdV
For an isothermal process, we know that PV=nRT. For one mole of gas, P=RTV.
dp=−RTV2dV
Substituting this into the bulk modulus expression:
B=−−RTV2dVdV=RTV2
Thus, the isothermal bulk modulus is:
B=RTV2
This matches with option (p): −RTV2.
The adiabatic bulk modulus Ba is given by:
Ba=−dpdV
For an adiabatic process, we have:
PVγ=constant
For a monoatomic gas, γ=53. Thus:
P=CV5/3
Differentiating gives:
dp=−5C3V8/3dV
Substituting into the bulk modulus expression:
Ba=−−5C3V8/3dVdV=5C3V8/3
Using C=PV5/3 and substituting back gives:
Ba=5P3V
This matches with option (q): −5P3V.
The slope of the P-V graph in an isothermal process is given by:
slope=dpdV
From the earlier derivation, we have:
dp=−RTV2dV
Thus:
dpdV=−RTV2
The slope is negative, and we can express it as:
slope=−RTV2
This matches with option (r): TV.
For the adiabatic process, the slope is given similarly:
slope=dpdV
From our earlier derivation:
dp=−5P3V8/3dV
Thus:
dpdV=−5P3V8/3
This matches with option (s): 4T3V.
Now we can summarize the matches:
- (A) Isothermal bulk modulus: (p) −RTV2
- (B) Adiabatic bulk modulus: (q) −5P3V
- (C) Slope of P-V graph in isothermal process: (r) TV
- (D) Slope of P-V graph in adiabatic process: (s) 4T3V
The final answer is:
- A → p
- B → q
- C → r
- D → s
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON40videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions66videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0282videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
The slope of P-V graph for isochoric process is
AZeroBInfiniteCOneDTwo - Question 2 - Select One
For the given P-V graph for an ideal gas, chose the correct V-T graph. Process BC is adiabatic.
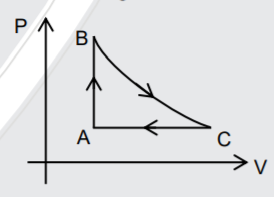 A
A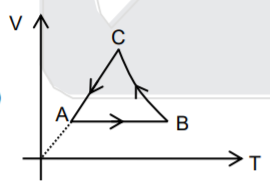 B
B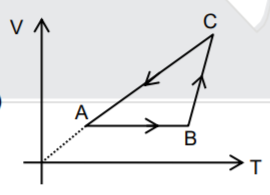 C
C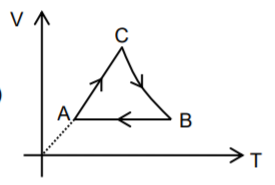 D
D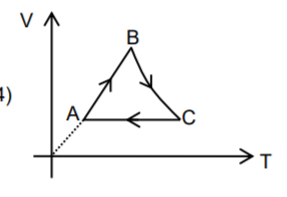
- Question 3 - Select One
For adiabatic processes (γ=CpCv)
APγV=constantBTγV=constantCTVγ−1=constantDTVγ=constant
Match the statement in Column I with the statements in Column II. One or more than one choice from Column II can match with a statement from Column I.
Column IColumn II(a)Young's modulus(p)−ΔVρV(b)Bulk modulus(q)FlAΔl(c)Compressibility(r)−Δd/dΔDl/l(d)Poisson's ratio(s)−ρVΔVView SolutionIn the V−T graph shown in figure:
_E01_152_Q01.png)
Column-IColumn-II(A)GasAis...andgasBis..., E is (p)monoatomic , diatomic(B)P_(A)/P_(B) is (q)diatomic , monoatomic(C)n_(A)/n_(B) is (r)gt1(s)lt1(t)cannot say any thingView SolutionAssertion: P v/s 1V graph is straight line for adiabatic process.
Reason: PV=constant for adiabatic process.View Solutionp−T curve for a cyclic process is as shown
P−V graph for this process will be:View SolutionAssertion: The graph between P V/s 1V is a straight line.
Reason: For adiabatic process P∝1VView Solution

