For a ideal monoatomic gas match the following graphs for constant mass in different processes (ρ = Density of gas)
_E01_156_Q01.png)
P=ρMwRT
For (A):
For ABP∝V⇒TαV2⇒T∝ρ−2
For BCV=constant⇒ρ=constant
For CAP=constant⇒ρT=constant
For (B)
For ABP∝T⇒ρ=constant
For BCT=constant⇒P∝ρ
For CAP=constant⇒ρT=constant
For (C)
For ABP=constant⇒ρT=constant
For BCT=constant⇒P∝ρ
For CAV=constant⇒ρ=constant
For(D)
For ABρ∝T⇒P∝T2
For BCT=constant⇒P∝ρ
For Aρ=constant⇒P∝T
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
40 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions
66 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Knowledge Check
For an ideal monoatomic gas, molar heat capacity at constant volume (Cv) is
A23RB32RC52RD25ROne moles of an ideal monoatomic gas undergo the state change as shown in following graph (ln 2 = 0.7)
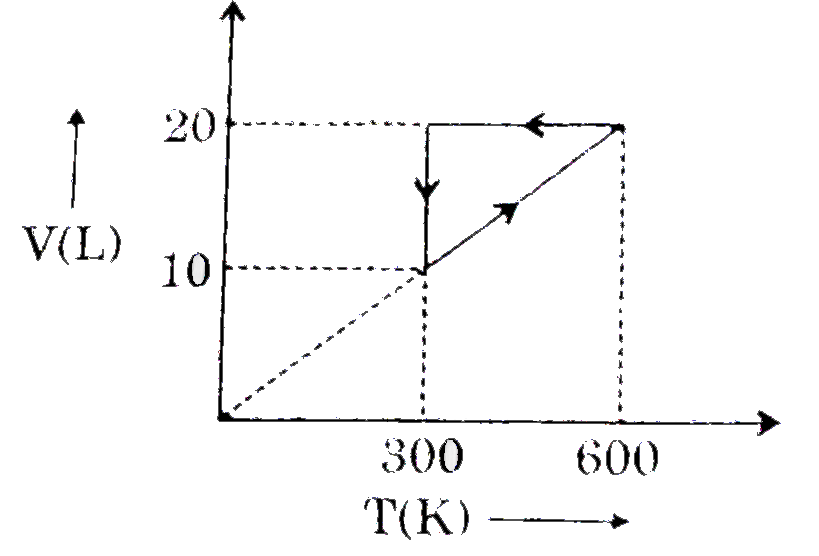
Correct graph for the process in paragraph is:A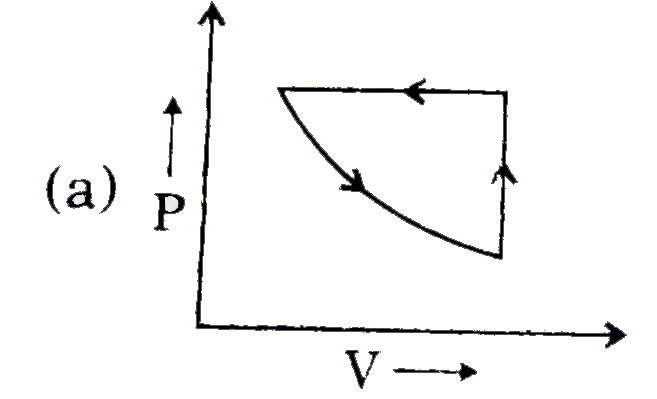 B
B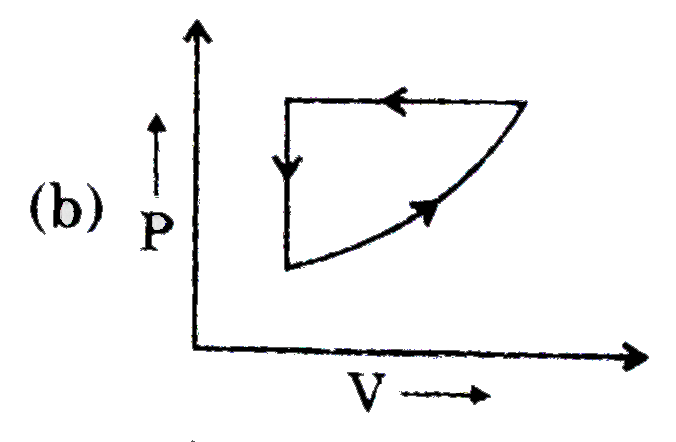 C
C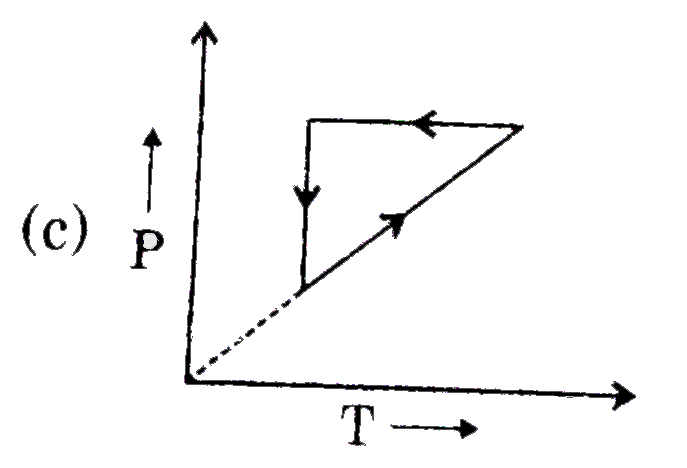 D
D
At a constant pressure, of the following graphs that one which represents the variation of the density of an ideal gas with the absolute temperature T, is
A B
B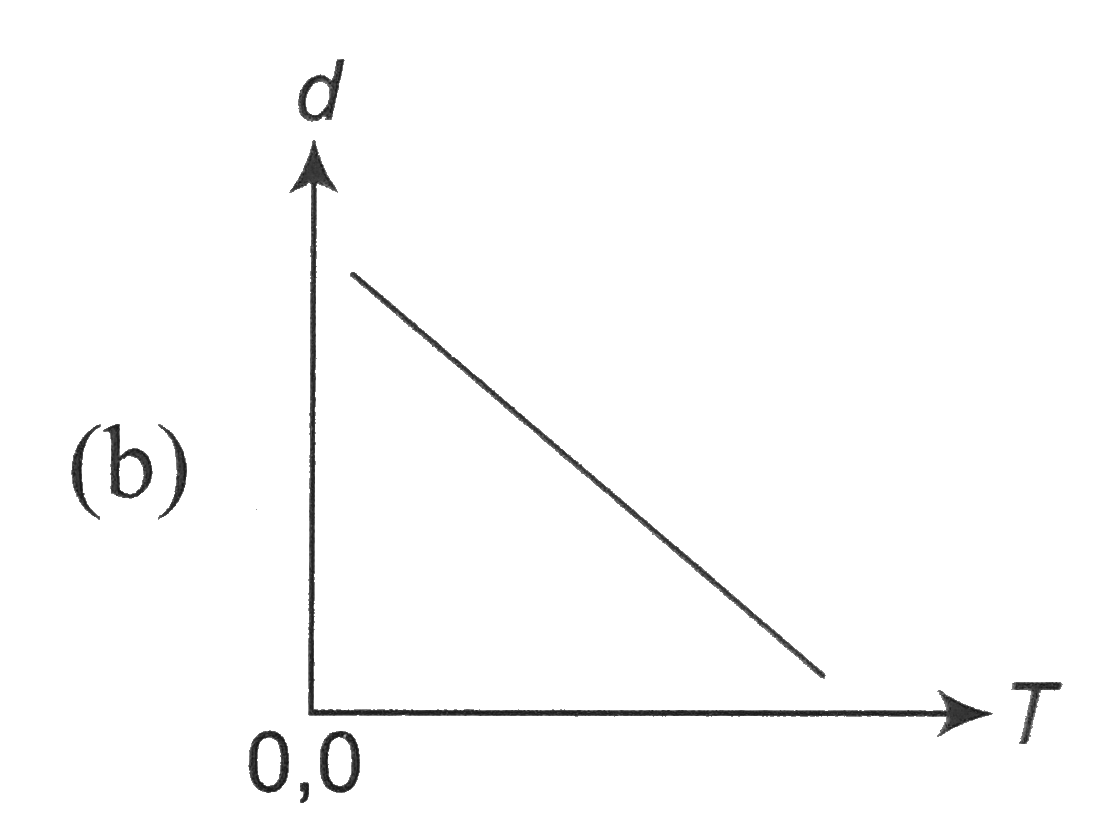 C
C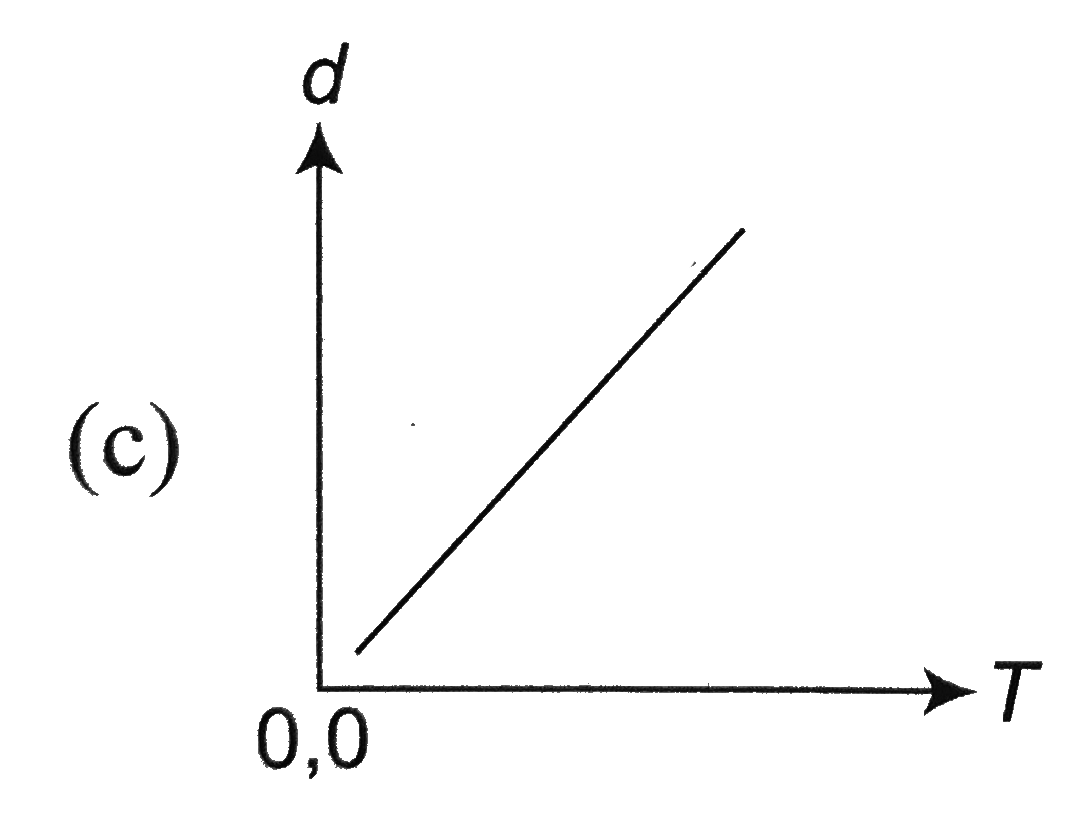 D
D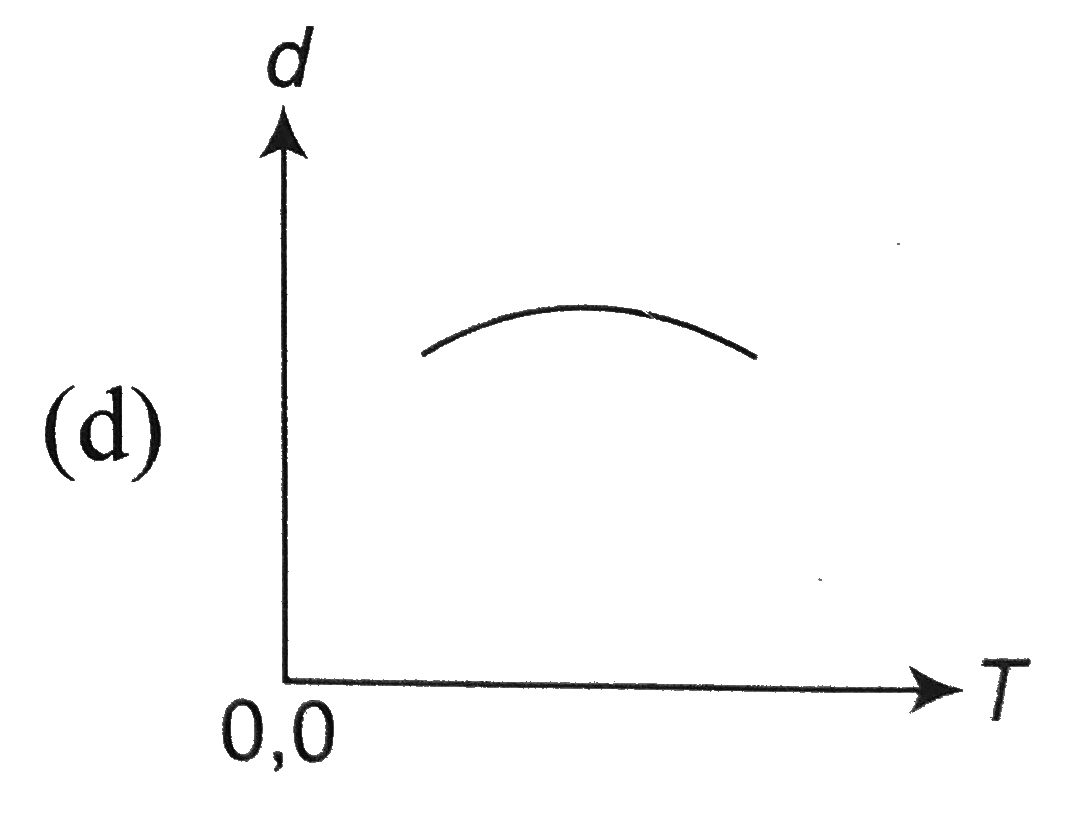
Match the following graphs of ideal gas with their coordinates :
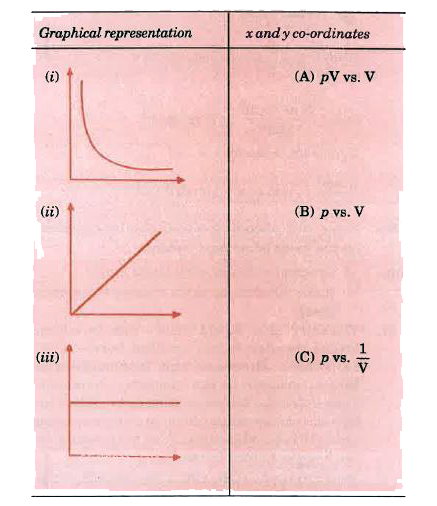
View SolutionAn ideal gas expands following a relation P2ρ= constant, where P = pressure and ρ = density of the gas. The gas is initially at temperature T and density ρ and finally its density becomes ρ3.
(a) Find the final temperature of the gas. (b) Draw the P – T graph for the process.
View SolutionA cyclic process of an ideal monoatomic gas is shown in figure. The correct statement is (are):
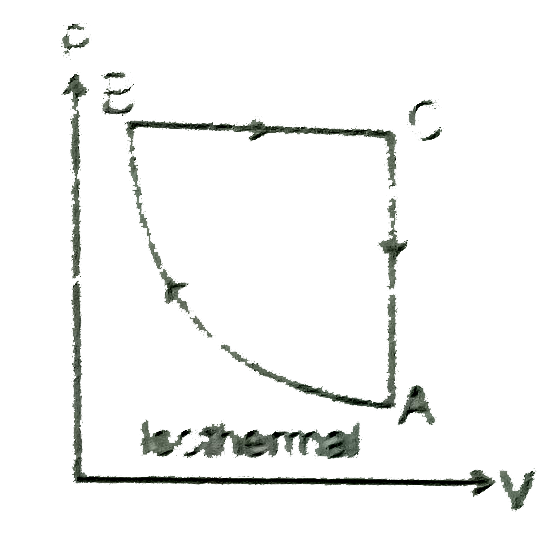
View SolutionAn ideal monoatomic gas is taken through one of the following reversible processes expressed by the equation in Table-1. Match the molar heat capacity of the gas, expressed in multiplies of R, in Table-2 with the appropriate process:
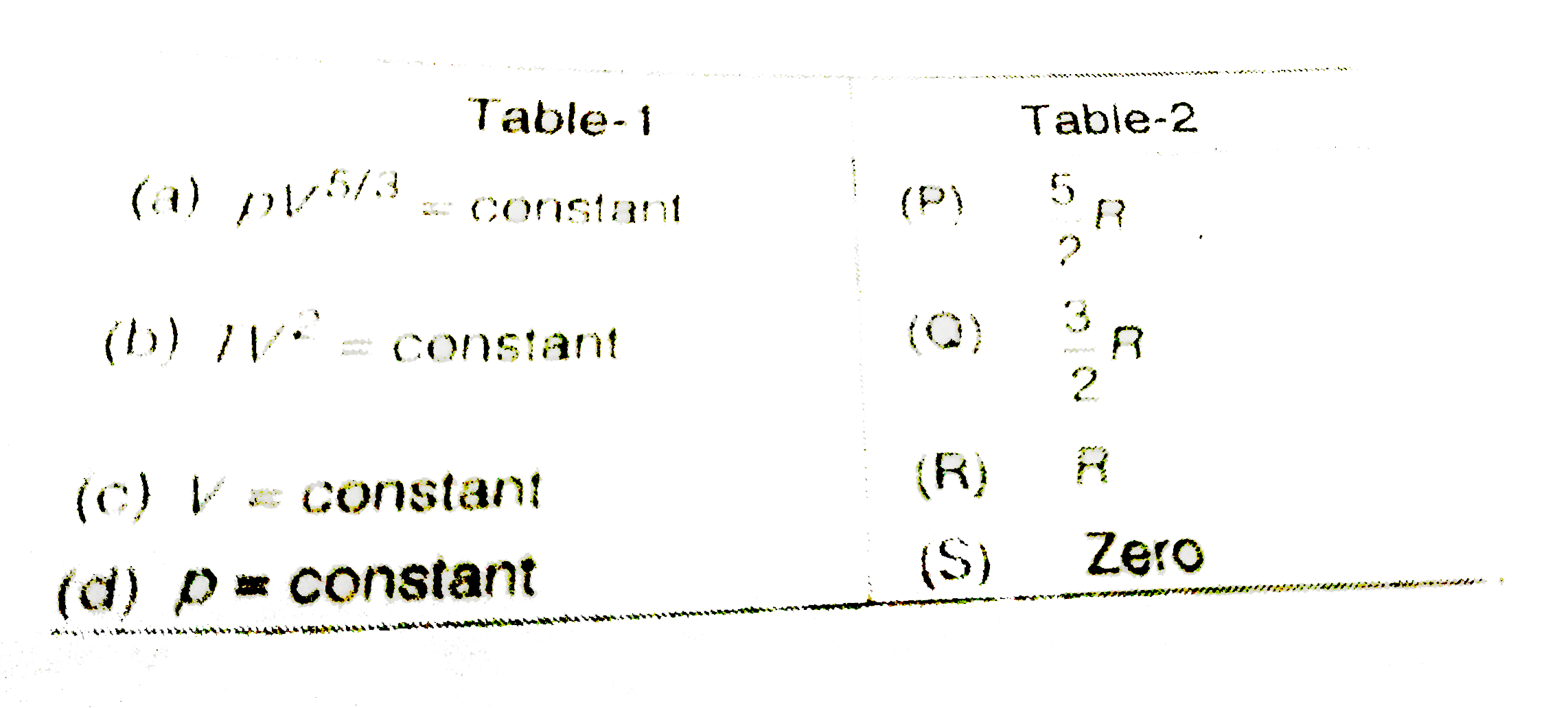
View SolutionA cyclic process of an ideal monoatomic gas is shown in figure. The correct statement is (are):

View Solution

