An ideal gas is taken through the following cyclic process. Process CD is isothermal & process DA is adiabatic
_E01_158_Q01.png)
List-IList-II(P)AB(1)heat exchanged is positive(Q)BC(2)change in temperature is negative(R)DC(3)coefficient of volume thermal expansion is undefined(S)DC(4)Adiabaticcompressibilityispositive
PQRS(A)1234
PQRS(B)4321
PQRS(C)2314
PQRS(C)3241
Step by step video & image solution for An ideal gas is taken through the following cyclic process. Process CD is isothermal & process DA is adiabatic {:(,"List-I",,"List-II"),((P),"AB" ,(1),"heat exchanged is positive" ),((Q),"BC" ,(2),"change in temperature is negative"),((R), "DC" ,(3),"coefficient of volume thermal expansion is undefined"), ((S),"DC" ,(4),Adiabatic compressibility is positive):} by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:ASSERTION-REASON
Explore 40 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:Comprehension Based Questions
Explore 66 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -02
Explore 82 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 427 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
Match the following
Column-IColumn-II(A)Isothermal process(p)Temperature changes(B)Isobaric process(q)Pressure changes(C)Isochoric process(r)Volume change(D)Cyclic process(s)Initial and final states are same
View Solution
An ideal gas undergoes a cyclic process, in which one process is isochoric, one process is isothermal and one process is adiabatic. During the isothermal process, 40 J heat is released by the gas, and during the isochoric process, 80 J heat is absorbed by the gas. if work done by the gas during adiabatic process is W1 and during isothermal process is W2 then the magnitude of W1W2 will be equal to:
View Solution
Knowledge Check
An ideal mono atomic gas is taken through the cyclic process shown in fig. Linear expansion from A to B following by adiabatic compression back to original state
 AEfficiency of cyclic process is zeroBDuring process A to B heat is released onlyCDuring process A to B heat is absorbed onlyDDuring linear process heat enters and leaves the process
AEfficiency of cyclic process is zeroBDuring process A to B heat is released onlyCDuring process A to B heat is absorbed onlyDDuring linear process heat enters and leaves the processMatch the List - I with List - II
List - IList - II(P)van Arkel method(1)Purification of copper(Q)Poling(2)Refining of silver(R)Cupellation(3)Manufacture of Na2CO3(S)Solvay process(4)Purification of titaniumAPQRS4132BPQRS2314CPQRS2341DPQRS4123An ideal gas expands from V to 2V in 4 separate processes. Where process 1 is isothermal process 2 is adiabatic, process 3 is free expansion and process 4 is isobaric. If E1,E2,E3 and E4 are the changes in average kinetic energy of the molecules in the isothermal, adiabatic free expansion and isobaric process respectively then choose the correct options.
AE2=E3BE1=E3CE1>E4DE4>E3
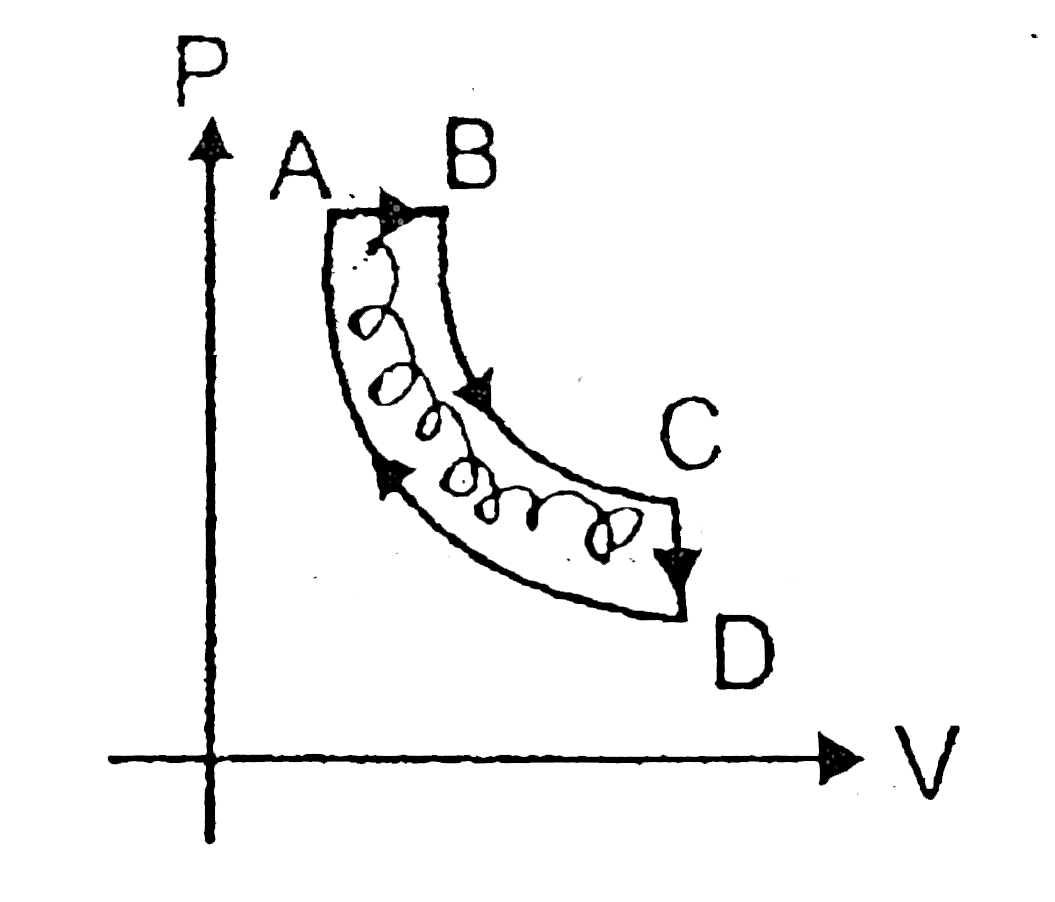
n moles of a monoatomic gas undergoes a cyclic process ABCDA as shown. Process AB is isobaric, process BC is adiabatic process CD is isochoric and process DA is isothermal the maximum temperature and minimum temperature in cycle are 4T0 and T0 respectively. Then:
View SolutionA gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gs in these three processes then
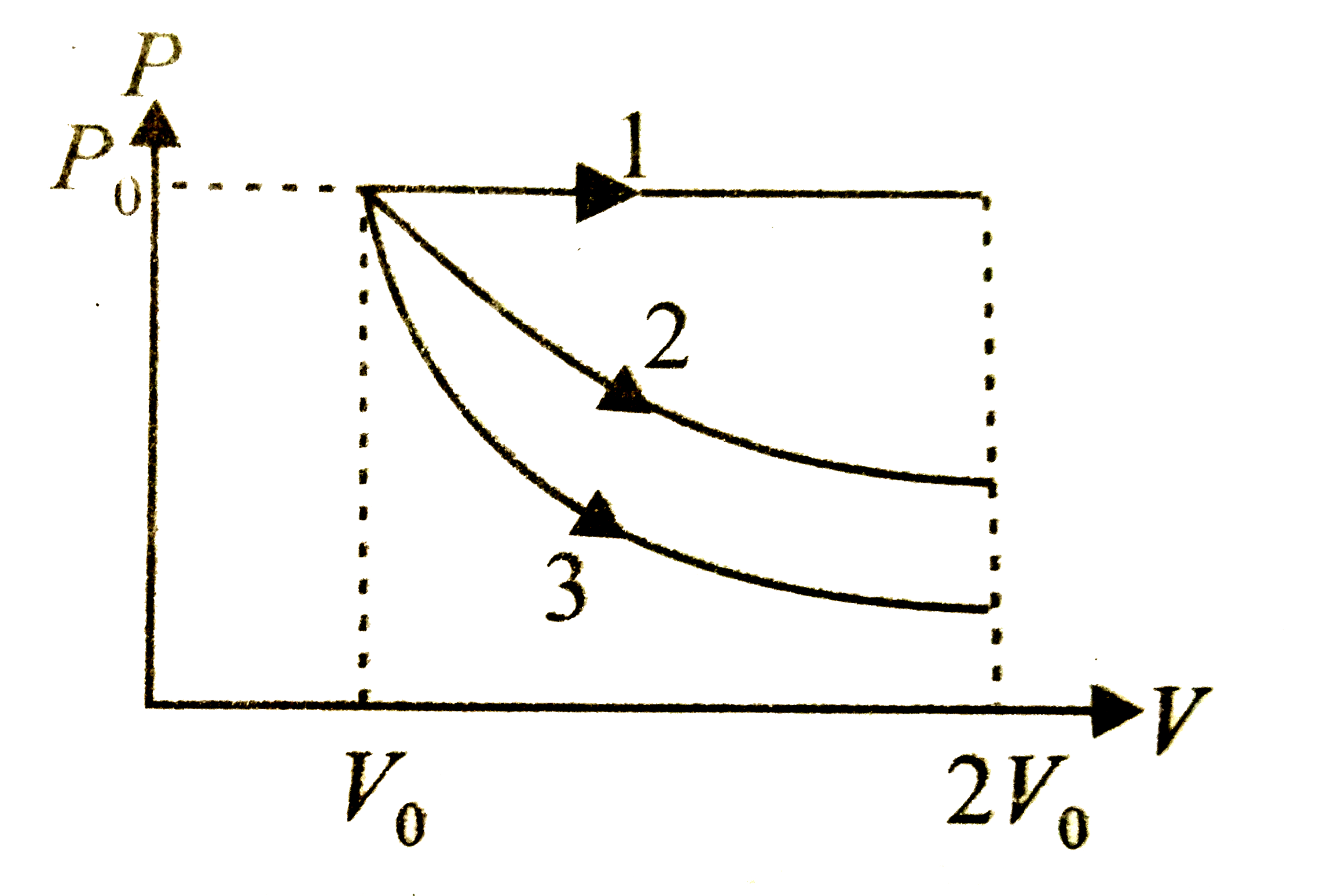
View SolutionA gas is expanded from volume V0 to 2V0 under three different processes, as shown in the figure. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let ΔU1,ΔU2 and ΔU3 be the change in internal energy of the gas in these three processes. Then
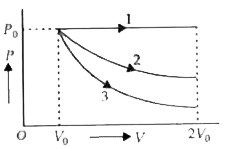
View SolutionA gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gs in these three processes then

View SolutionThe graph shown below is a graph between work done on the gas versus heat supplied to it. Different lines OA, OB, OC, OD represent different processes on monoatomic gas or a diatomic gas. Match the correct process with the line.

List IList IIP. OA1. Adiabatic ProcessQ. OB2. Isobaric process for monoatomic gasR. OC3. Isothermal processS. OD4.Isobaric process for diatomic gas
View Solution
