Two non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
(##JMA_CHMO_C10_027_Q01##).
(a) Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
(b) If the whole is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the period of these oscillations.
The correct Answer is:A, B, C
(a) Let the liqud of density 1.5ρ occupy the lect portion AB and the liquid of density ρoccupy the right portion BC of the tube. The pressure at the lowest point D due to the liquid on the left is
P1=(R−Rsinθ)1.5ρg
_E01_113_S01.png)
The pressure due to the liquid on the right is
P2(Rsinθ+Rcosθ)ρg+(R−Rcosθ)1.5ρg
Since the liquids ar in equilibrium
P1=P2 or (R−Rsinθ)1.5ρg=(R−Rcosθ)ρg+(R−Rcosθ)1.5ρg
Solving, we get
tanθ=0.2 or θ=tan−1(0.2)
(b) Let the whole liquid lbe given a small angular displacement α towards right. Then the pressure difference between the right and the left limbs is
dP=P2−P1
=[Rsin(θ+α)+Rcos(θ+α)ρg+[R−Rcos(θ+α)1.5ρg−[R−Rsin(θ+α)]1.5ρg
=Rρg[2.5sin(θ+α)−0.5cos(θ+α)]
=Rρg[2.5(sinθcosα+cosθsinα)−0.5(cosθcosα−sinθsinα)]
For small α
sinα=α,cosα≅1∴dP=Rρg
[2.5sinθ+2.5αcosθ−0.5cosθ+0.5αsinθ]
As tanθ=0.2,sinθ0.2√1.04≈0.2,cosθ=1√1.04≈1
∴dP=Rρg[2.5×0.2+2.5α−0.5+0.5×0.2α]
=Rρg[2.6α]
=236ρg
where y=Rα, the linear displacement
∴ Restoring force F=2.6ρgAy
This shows that F∝y
Hence the motion is simple harmonic with force constant
k=2.6ρgA
Now, total mass of the liquid
m=2πR4Aρ+2πR4A(1.5p)=5πRAρ4
∴ Time period
T=2π√mk=2π√5πrAρ4×236ρgA=π√1.93πR9.8
=2.47√R seconds.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05(B)
46 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 04[A]
25 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Two non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.
(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.
View SolutionTwo non-viscous, incompressible and immiscible liquids of densities p and 1.5p are poured into the two limbs of a circular tube of radius R and small cross section kept fixed in a vertical plane as shown in the figure. Each liquid occupies one fourth the circumference of the tube.
(i)Find the angle theta that the radius to the interface makes with the vertical in equilibrium position. _________
(ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations. ____________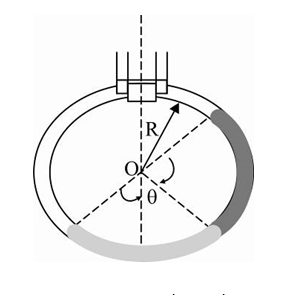
View Solution
Knowledge Check
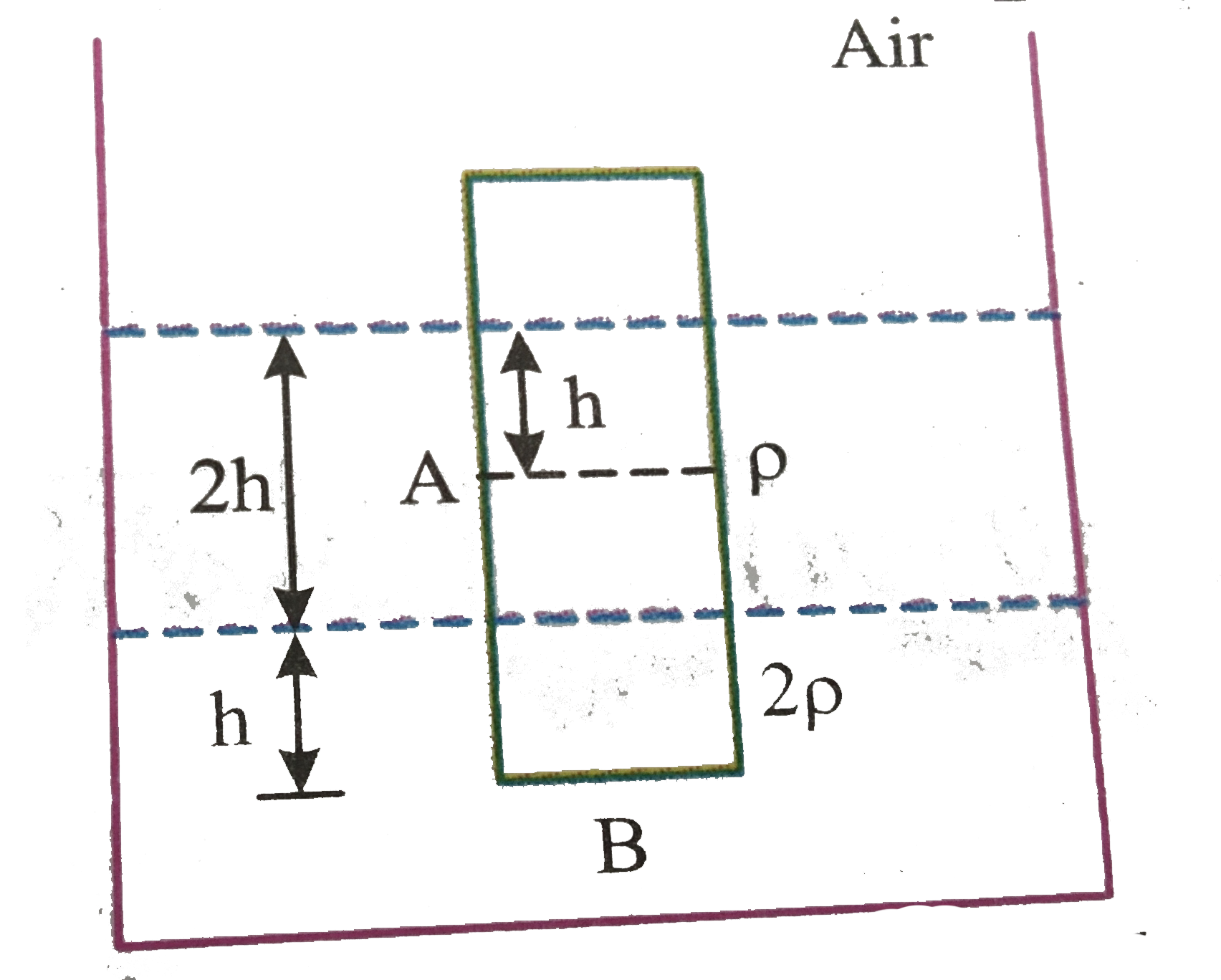
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:A2πghB3ρghC4ρghDnoneA V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrium the level of liquid in both limbs of tube are equal. Find the angular frequency of small oscillation of liquid.
Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of theseA uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is
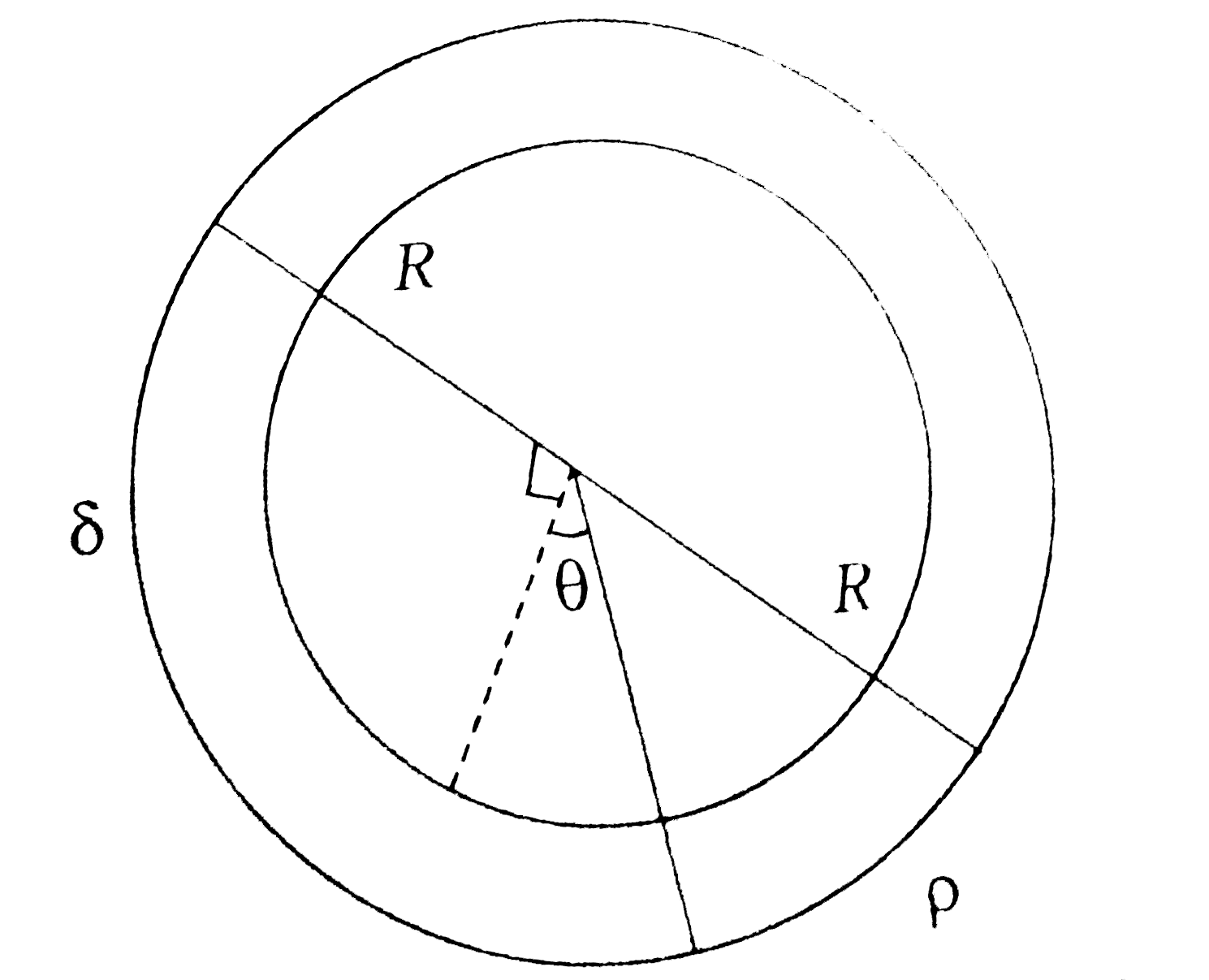Atan−1(ρ−δρ+δ)Btan−1(ρδ)Ctan−1(δρ)Dtan−1(ρ+δρ−δ)
Two immiscible liquids of densities ρ and 2ρ and thickness (heights) h and 2h, respectively, push a vertical plate. Find the total side thrust given by the liquids on the vertical plate.
View SolutionA thin triangular glass tube containing immiscible liquids A, B, C of densities ρ,2ρ,3ρ is at rest in vertical plane. Find x.
View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.
View SolutionA small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
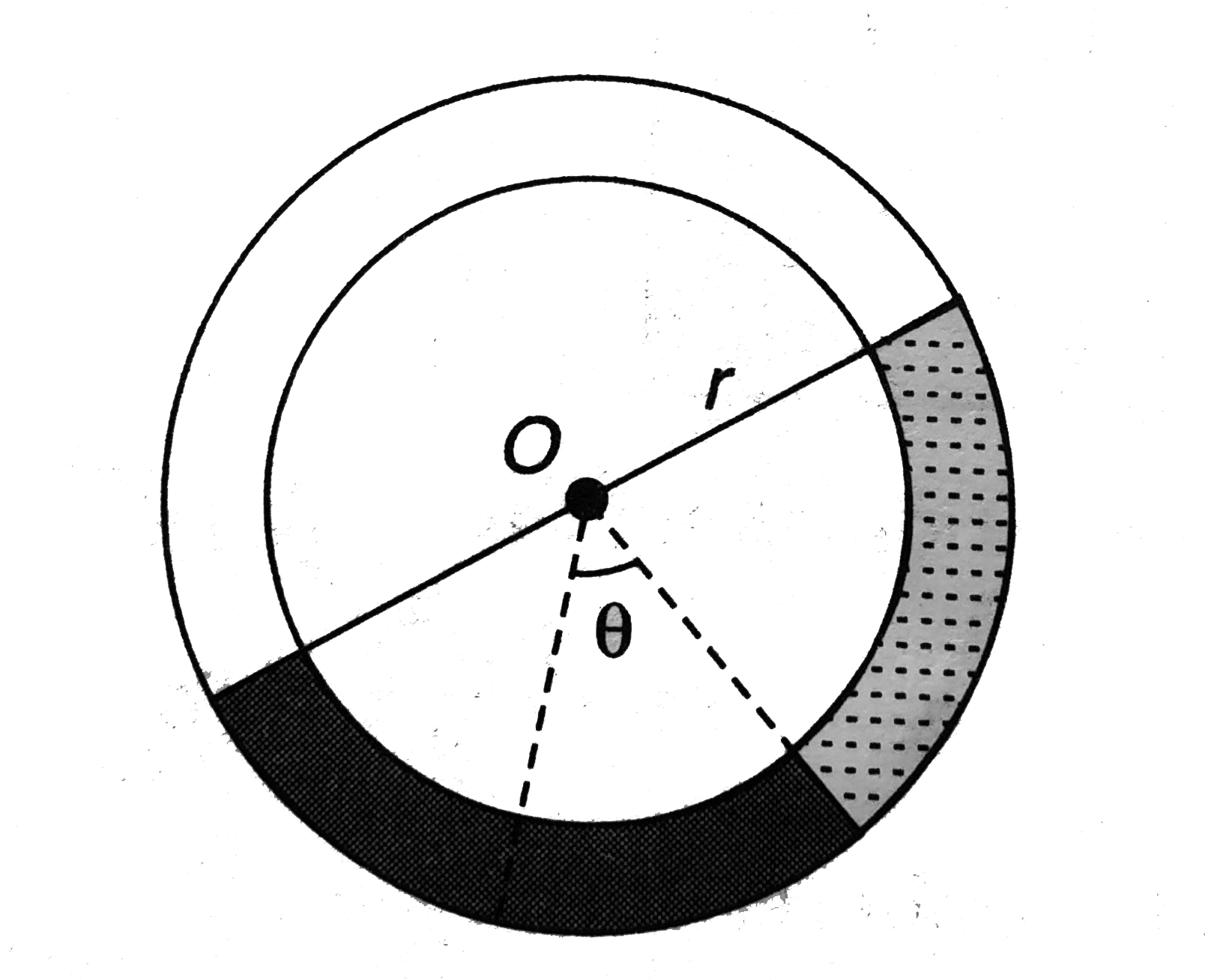View SolutionA thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2(ρ1>ρ2) fill half the circle. The angle θ between the radius vector passing though the common interface and the vertical is :
View Solution