The acceleration of a particle depends on displacement covered in a time as $a = s + 5$ . It is given that initially $s = 0$ and $v = 5 m / s$ , then which of the following is possibly correct ?

A

$v = s + 5$

B

$v = \sqrt{s + 5}$

C

$v = {log}_{e} {(\frac{s + 5}{5})}^{2}$

D

$v = {log}_{e} (\frac{s + 5}{s})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$a = s + 5$
$v \frac{d v}{d s} = + 5$
$v \int s v d v = s \int 0 v d s + s \int s 5 d s$
${[\frac{v}{2}]}_{s}^{v} = \frac{s^{2}}{2} + 5 s$
$\frac{v^{2} - 2 s}{2} = \frac{s^{2} + 10 s}{2}$
$v^{2} = s^{2} + 10 s + 2 s$
$v^{2} = {(s + 5)}^{2}$
$v = \pm (s + 5)$
$v = s + 5$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The acceleration a of $α$ of a particle depends on displacements covered in a time t as $a = S + 5$ . It is given that initially $S = 0$ m and $v = 5 m / s$ . Then

A $v = S + 5$
B $v = \sqrt{S + 5}$
C $t = {log}_{e} (\frac{S + 5}{S})$
D $t = {log}_{e} (\frac{S + 5}{5})$
Question 2 - Select One
If acceleration of a particle at any time is given by $a = 2 t + 5$
Calculate the velocity after 5 s, if it starts from rest
A $50 m s^{- 1}$
B $25 m s^{- 1}$
C $100 m s^{- 1}$
D $75 m s^{- 1}$
Question 3 - Select One
The acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is $- 5 m / s$ , the velocity at t = 8 s is

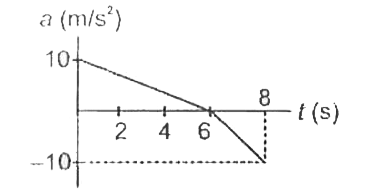A $+ 15 m / s$
B $+ 20 m / s$
C $- 15 m / s$
D $- 20 m / s$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile