A ball is projected towards right from point A at an angle $θ$ with vertical. A system imparts an acceleration $g tan θ$ to the ball towards left along negative x-axis. The ball will return to ground at :

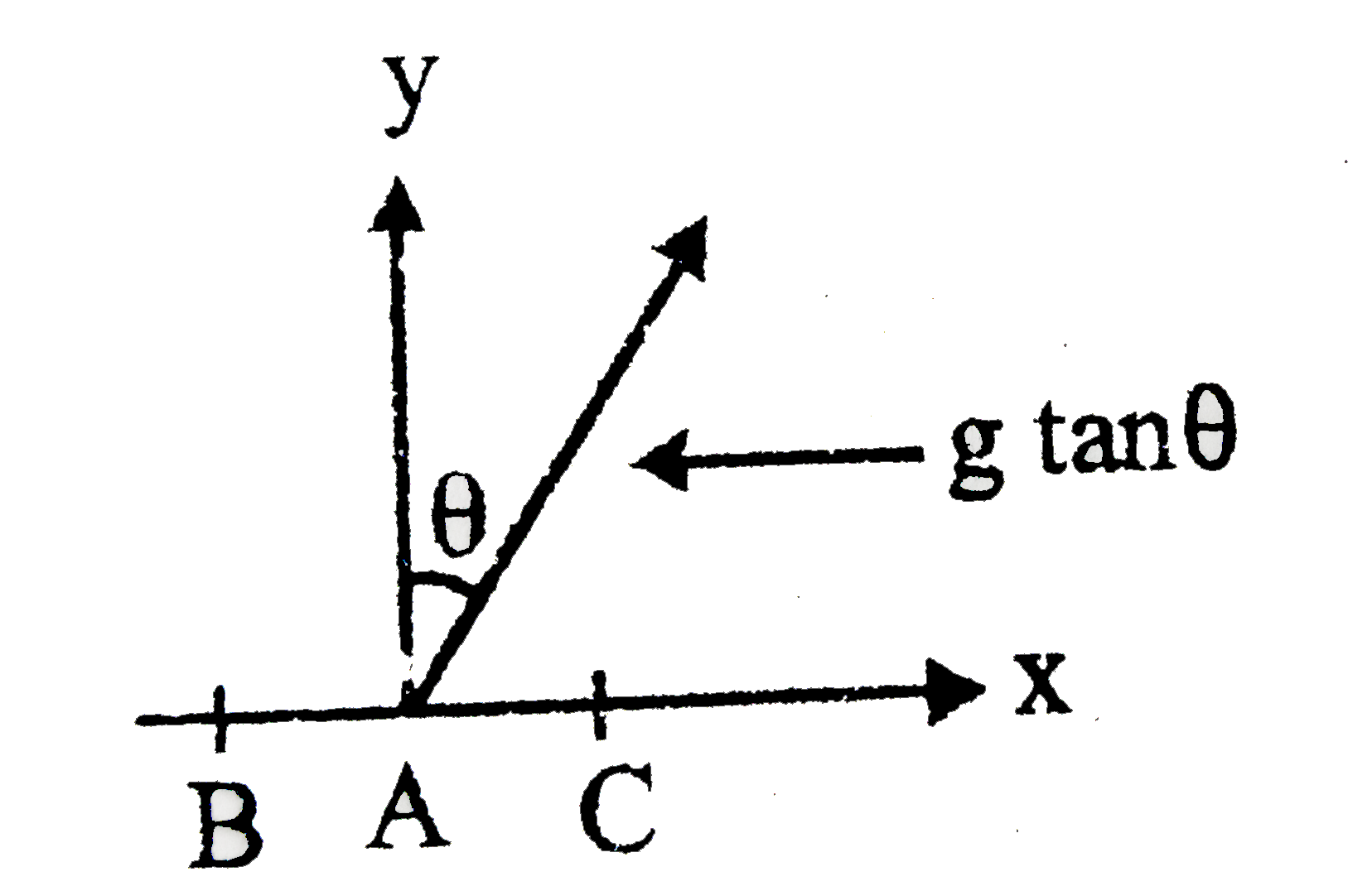
A

A

B

B left to point A

C

C right to point A

D

None of the above

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$T = \frac{2 u sin (90^{\circ} - θ)}{g} = \frac{2 u cos θ}{g}$
$s_{n} = u_{x} T + \frac{1}{2} a_{x} T^{2}$
$= u sin θ x \frac{2 u cos θ}{g} + \frac{1}{2} (- g tan θ) {(\frac{2 u cos θ}{g})}^{2}$
$= \frac{u^{2} sin θ}{g} - \frac{1}{2} g . \frac{sin θ}{cos θ} \times \frac{4 u^{2} {cos}^{2} θ}{g^{2}}$
$= \frac{u^{2} sin 2 θ}{g} - \frac{u^{2} sin 2 θ}{g}$
Hence particle returnes to A.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ball is projected from ground with a velocity $V$ at an angle $θ$ to the vertical. On its path it makes an elastic collison with a vertical wall and returns to ground. The total time of flight of the ball is
A $\frac{2 v sin θ}{g}$
B $\frac{2 v cos θ}{g}$
C $\frac{v sin 2 θ}{g}$
D $\frac{v cos θ}{g}$
Question 2 - Select One
A ball is projected from ground with a velocity V at an angle $θ$ to the vertical. On its path it makes an elastic collision with a vertical wall and returns to ground. The total time of flight of the ball is
A $\frac{2 v sin θ}{g}$
B $\frac{2 v cos θ}{g}$
C $\frac{v sin 2 θ}{g}$
D $\frac{v cos θ}{g}$
Question 3 - Select One
A cylindrical hall has a horizontal smooth floor. A ball is projected along the floor from A point on the wall in a direction making an angle $θ$ with the radius through the point the ball returns bak to the initial point after two impacts with the wall. if the coefficient of restitution is e than ${tan}^{2} θ$ will be
A $\frac{1 + e + e^{2}}{e^{3}}$
B $\frac{1 + e}{e^{2}}$
C $\frac{e^{2}}{1 + e}$
D $\frac{e^{3}}{1 + e + e^{2}}$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile