ABCD is a smooth fixed vertcal circular track. A small particle is projected tangentially from the lowermost point A of the track with speed u√4gr where r is the radius of track. AC is the vertical diameter of track, then -
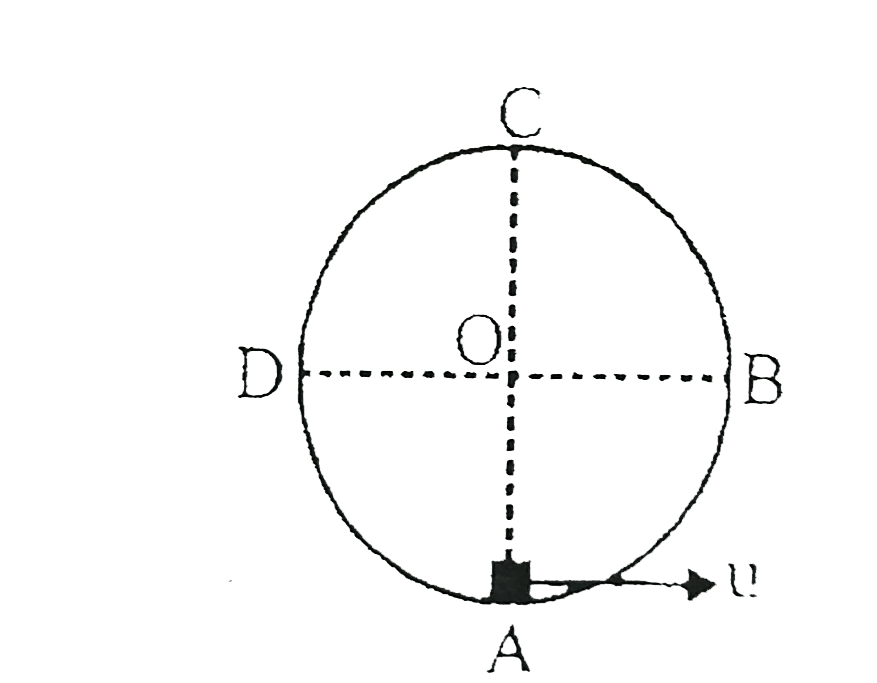
The particle leaves the track some where between B and C on the path of track.
The particle cannot hit the point C when it is moving in air.
The particle cannot cross the line AC when it moving in horizontal direction
The particle cannot cross the line BD while moving vertically.
The correct Answer is:A, B, C
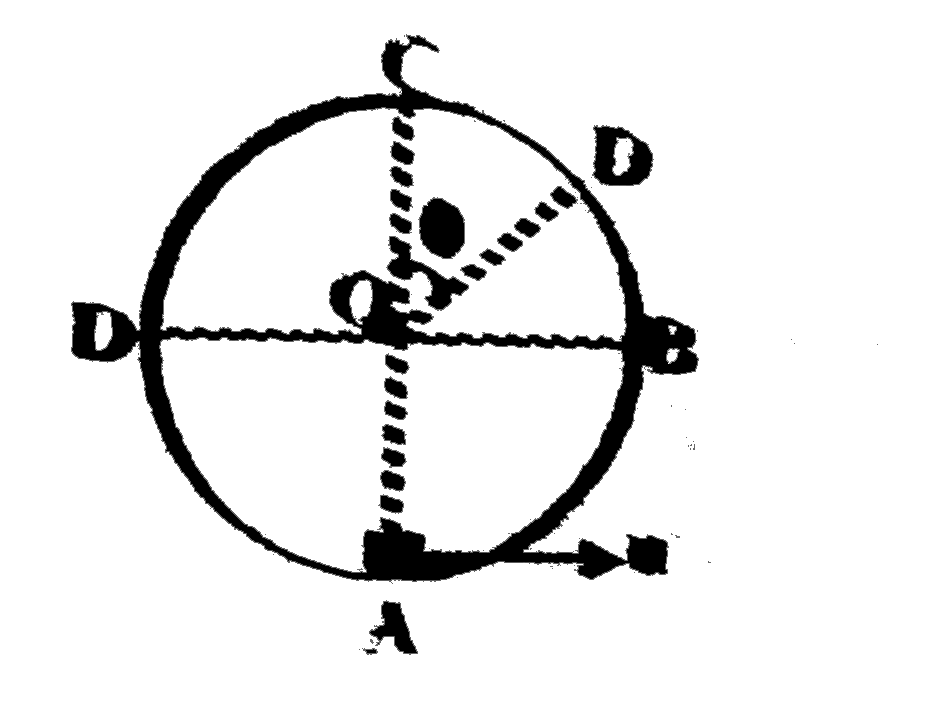
(A), (B) umin is √5gr to complete the verticle circle in this case
So, the particle leaves the track at some angle θ at point D shown between B & C
(C ) After that it follows parabloic path whose maximum height is less than OC and will not cross AC horizintally then.
(D) The particle is moving vertically up when it passes through B.
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICA PART B1videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICA PART C5videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART B3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A man running along a circular track has the speedof 10 km per hour. A source of light is at the centre of the circular track. A wall is along the tangent to the circular track at the point from which he starts.What is the speed of the shadow of the man on the wall when he covers 18th of the track? (Assume thetrack to be a line.)
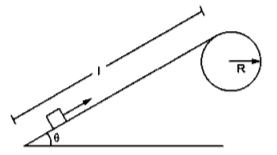
View SolutionFigure shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. a.Find the minimum projected speed v0 for which the particle reaches the top of the track. b. Assuming that the projection speed is 2v0 and that the block does not lose contact with the track before reading its top, find the force acting on it when it reaches the top. c. Assuming that the projection speed is only slightly greater than v0 where will the block lose contact with the track?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
As shown below AB represents an infinite wall tangential to a horizontal semi-circular track. O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with a speed v starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively V and a, then :
 AV=vcos(vtR)BV=vsec2(vtR)Ca=(v2R)sec2(vtR)tan(vtR)Da=(2v2R)sec2(vtR)tan(vtR)
AV=vcos(vtR)BV=vsec2(vtR)Ca=(v2R)sec2(vtR)tan(vtR)Da=(2v2R)sec2(vtR)tan(vtR) - Question 2 - Select One or More
As shown in figure AB represents an infinite wall tangential to a horizontal semi circular track.O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with speed v starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively 'V' and 'a' then,
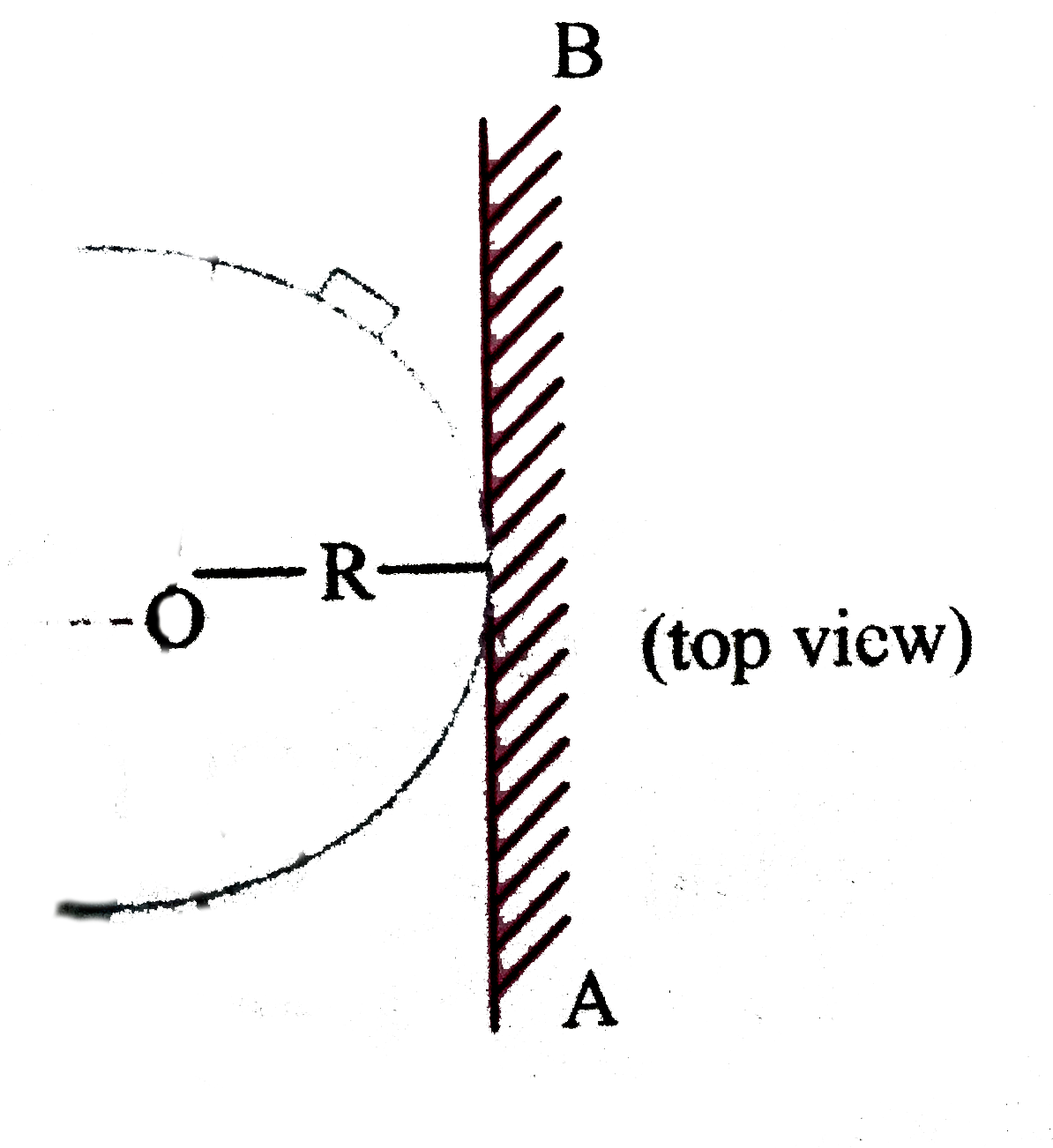 AV=vcosvtRBV=vsec2(vtR)Ca=v2Rsec2(vtR)tan(vtR)Da=2v2Rsec2(vtR)tan(vtR)
AV=vcosvtRBV=vsec2(vtR)Ca=v2Rsec2(vtR)tan(vtR)Da=2v2Rsec2(vtR)tan(vtR) - Question 3 - Select One
Figure shows a smooth vertical circular track AB of radius R. A block slides along the surface AB when it is given a velocity equal to √6gR at point A. The ratio of the force exerted by the track on the block at point A to that at point B is
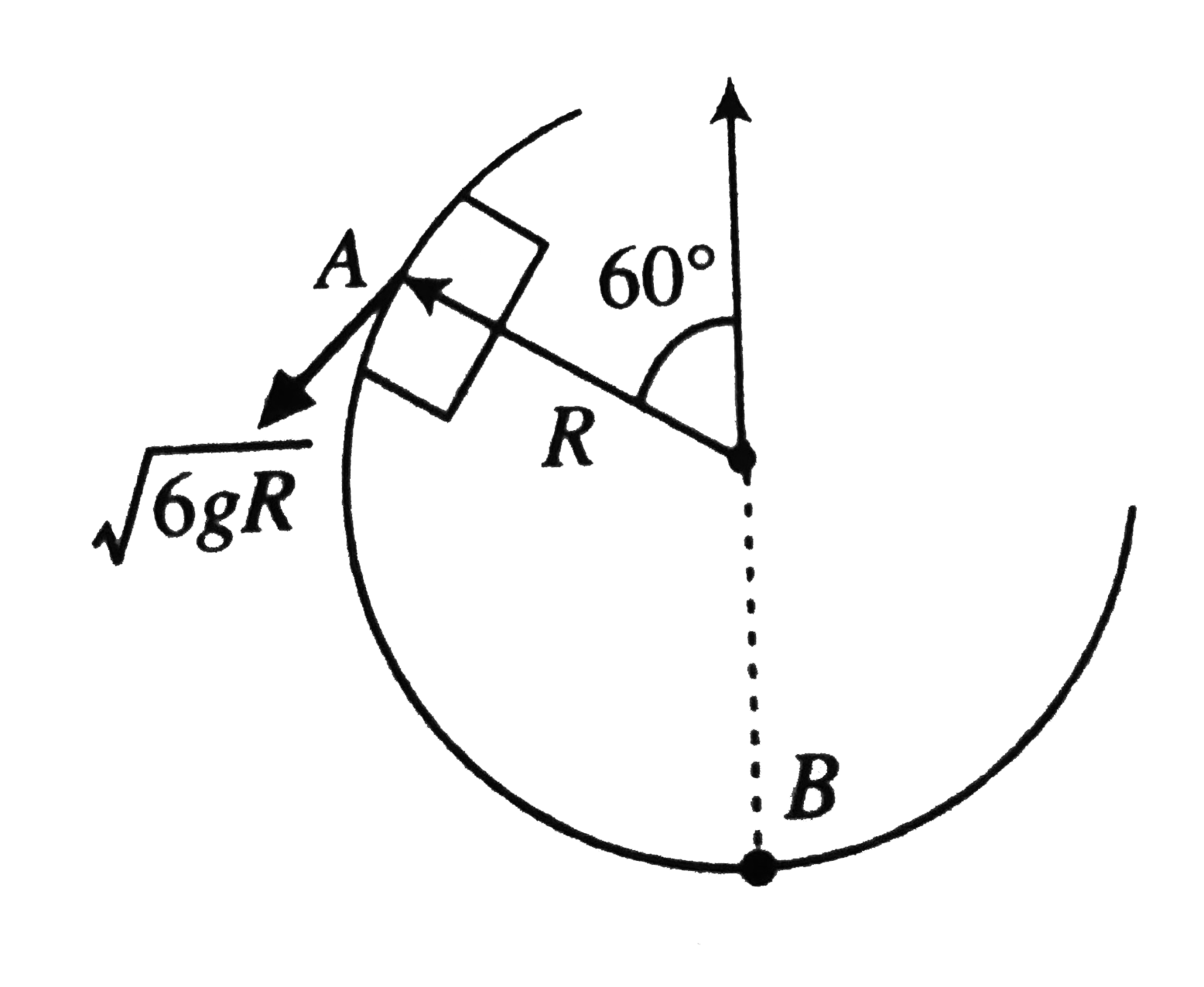 A0.25B0.35C0.45D0.55
A0.25B0.35C0.45D0.55
A smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length 3R/4 is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant K=mg/R. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.
 View Solution
View SolutionIn a fixed quarter circular track of radius R which lies in a vertical plane, a block is released from point A and it leaves the path at point B. The radius of curvature of its trajectory when it just leaves the path will be
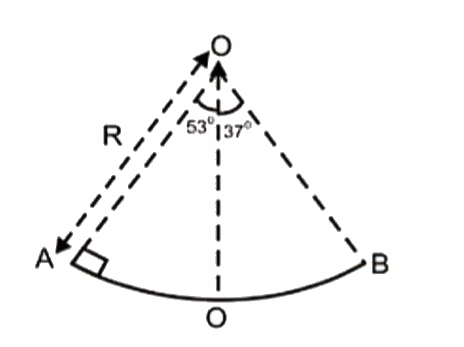 View Solution
View SolutionIn a park there are three concentric circular running tracks. Radius of 2 nd track is double of the first and of 3rd track is triple of the first. Three runners are running on these tracks with constant speed. When the runner in the first track completes one round, the runner in 2nd has completed half round and the runner in third track has completed quarter round. If the accelerations of the runners are in ratio α:β:γ, where α,β and γ are least integers, then find the value of α+β+γ9.
View SolutionA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
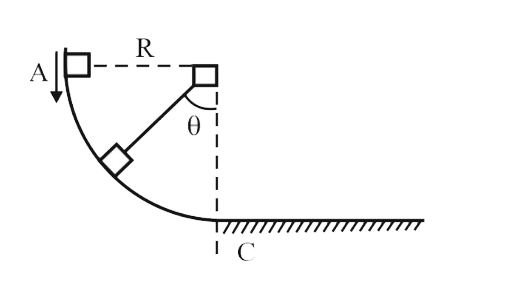 View Solution
View SolutionA smooth semicircular wire track of radius R if fixed in a vertical plane. One end of massless spring of netural length 3R4 is attached to the lowest point O of the wire track. A small ring of mass m which can slide on the track is attched to the other end of the spring. the ring is held stationary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant is K=mgR. considering the instance when the ring is released, the free body diagram of the ring, when aT is tengential acceleration, F is restoring force and N is normal reaction is
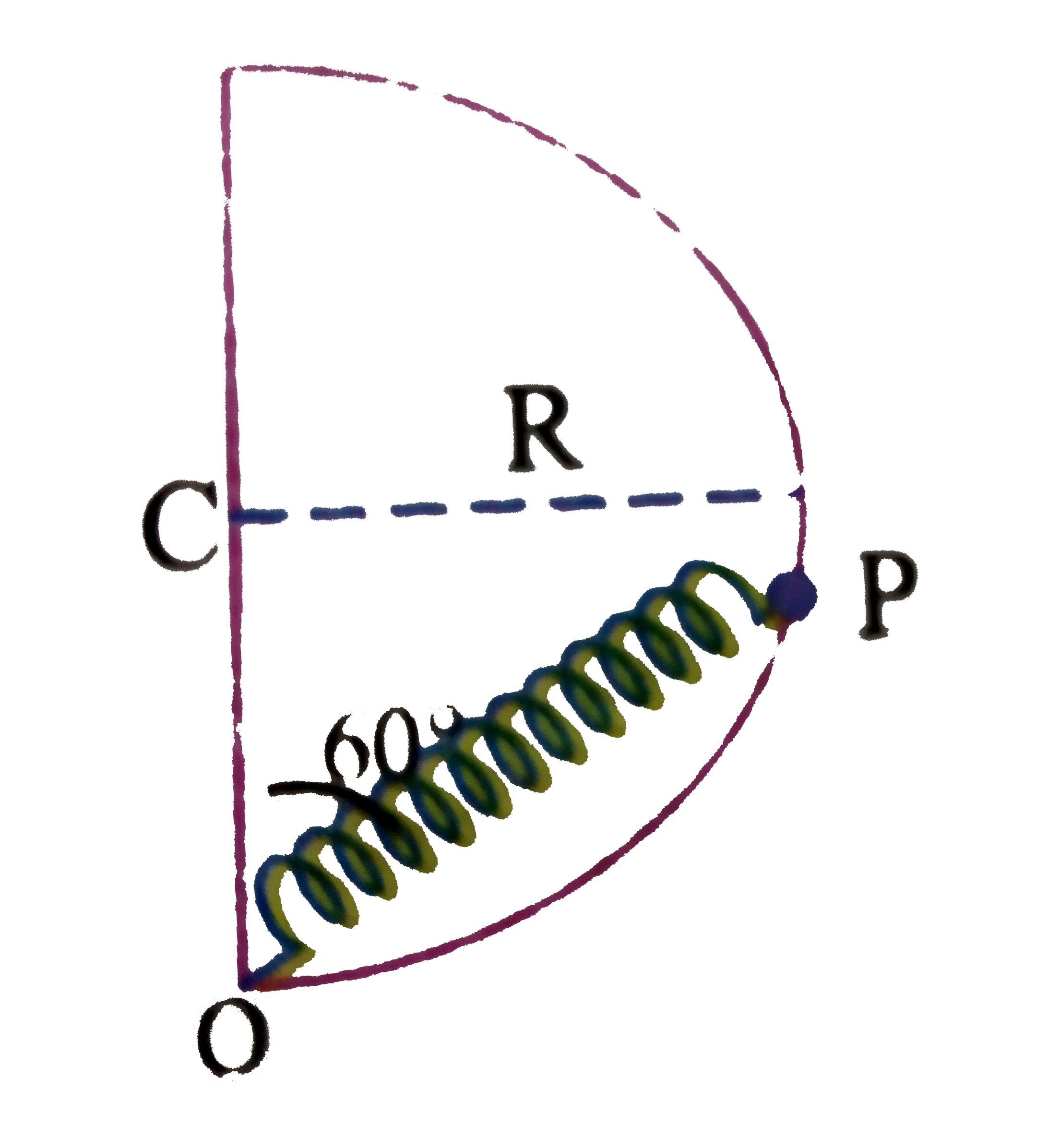 View Solution
View Solution

