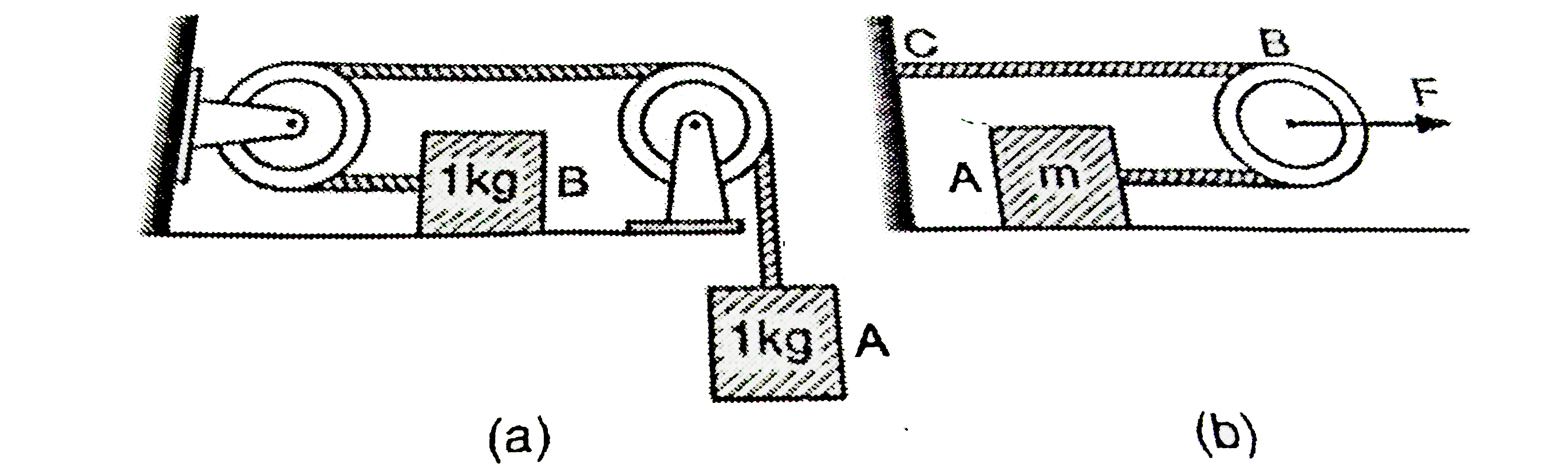Suppose we consider friction between string and the pulley while still considering the string to be massless. So, in such a theoretical case, the tension in the string in contant with the pulley will not be constant and its variation is calculated as follows.
If the string is just on the verge of slipping on the pulley, then friction acting is limiting and if T2>T1 then friction will act towards T1 in tangential direction as shown.

dN=(T+df)sin(dθ/2)+(T+dT)sin(dθ/2)
dN=Tsin(dθ/2)+dfsin(d∂/2)+Tsin(dθ/2)+dTsin(dθ/2)
dN≈2Tsin(dθ/2)
dN≈2Tdθ2
dN=Tdθ ........(1)
Alsso, (T+df)cos(dθ2)=(T+dT)cos(dθ2)
Tcos(dθ2)+dfcos(dθ2)=Tcos(dθ2)1dTcos(dθ2)
df=dT=μdN.........(2)
from (1) & (2)
dT=μTdθ
∫T2T1dTT=μ∫θ0dθ
ln(T2T1)=μθ
T2=T1eμθ, where θ is the angle of contact between the string and the pulley Based on above information, answer the following questions.
Two masses m1kg and m2kg passes over an atwood machine. Find the ratio of masses m1 and m2 so that string passing over the pulley will just start slipping over its surface. The friction coefficient between the string and pulley surface is 0.2.
A
e0.2π
B
e0.2
C
0.2
D
e0.4π
Video Solution
Text Solution
The correct Answer is:A
For a simple at wood's machine we can write for the two masses
m1g−T1=m1a
and T2−m2g=g=m2a
and if string starts slipping, we have
T1=T2eμπ
or m1(g−a)=m2(g+a)eμπ
If sting just slips. we can use a=0, thus we have
m1m2=e0.2π
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICA PART B1videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICA PART C5videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART B3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
Suppose we consider friction between string and the pulley while still considering the string to be massless. So, in such a theoretical case, the tension in the string in contant with the pulley will not be constant and its variation is calculated as follows.
If the string is just on the verge of slipping on the pulley, then friction acting is limiting and if T2>T1 then friction will act towards T1 in tangential direction as shown.

dN=(T+df)sin(dθ/2)+(T+dT)sin(dθ/2)
dN=Tsin(dθ/2)+dfsin(d∂/2)+Tsin(dθ/2)+dTsin(dθ/2)
dN≈2Tsin(dθ/2)
dN≈2Tdθ2
dN=Tdθ ........(1)
Alsso, (T+df)cos(dθ2)=(T+dT)cos(dθ2)
Tcos(dθ2)+dfcos(dθ2)=Tcos(dθ2)1dTcos(dθ2)
df=dT=μdN.........(2)
from (1) & (2)
dT=μTdθ
∫T2T1dTT=μ∫θ0dθ
ln(T2T1)=μθ
T2=T1eμθ, where θ is the angle of contact between the string and the pulley Based on above information, answer the following questions.
Figure shows a cylinder mounted on an horizontal axle. A massless string is wound on it with two and a half turns and connected to two masses m and 2m. If the system is in limiting equilibrium, find the coefficient of friction between the string and the pulley surface.
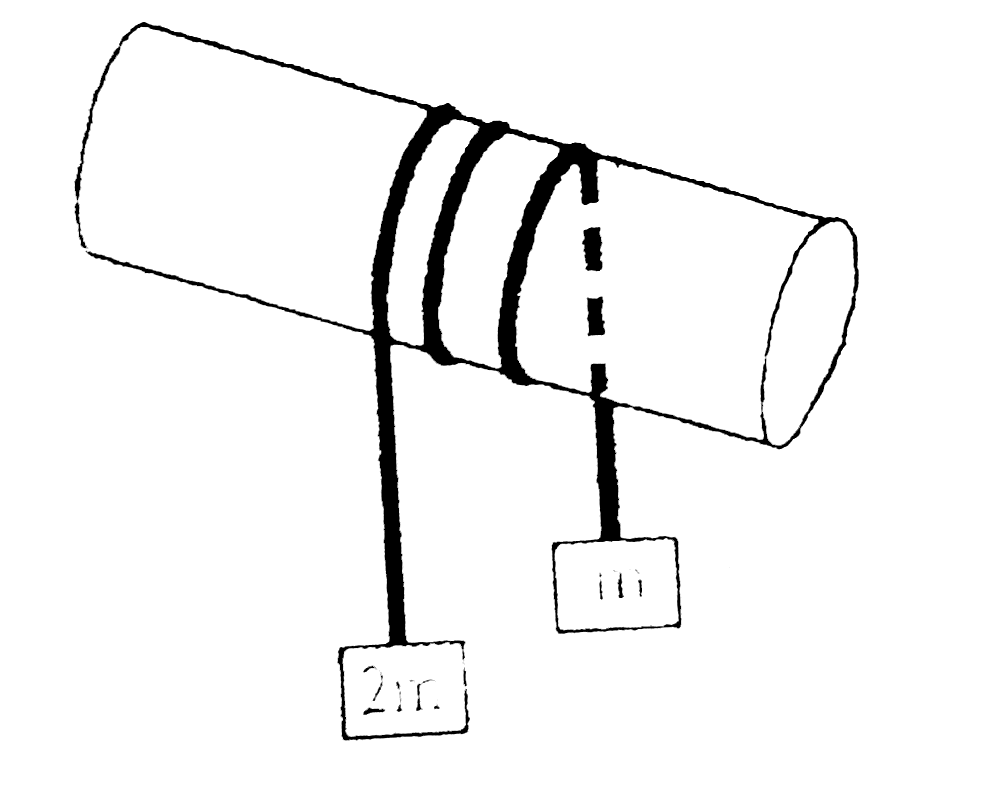 A15π1n(2)B25π1n(2)C110π1n(2)D13π1n(2)
A15π1n(2)B25π1n(2)C110π1n(2)D13π1n(2) - Question 2 - Select One
The tension in the string in the pulley system shown in
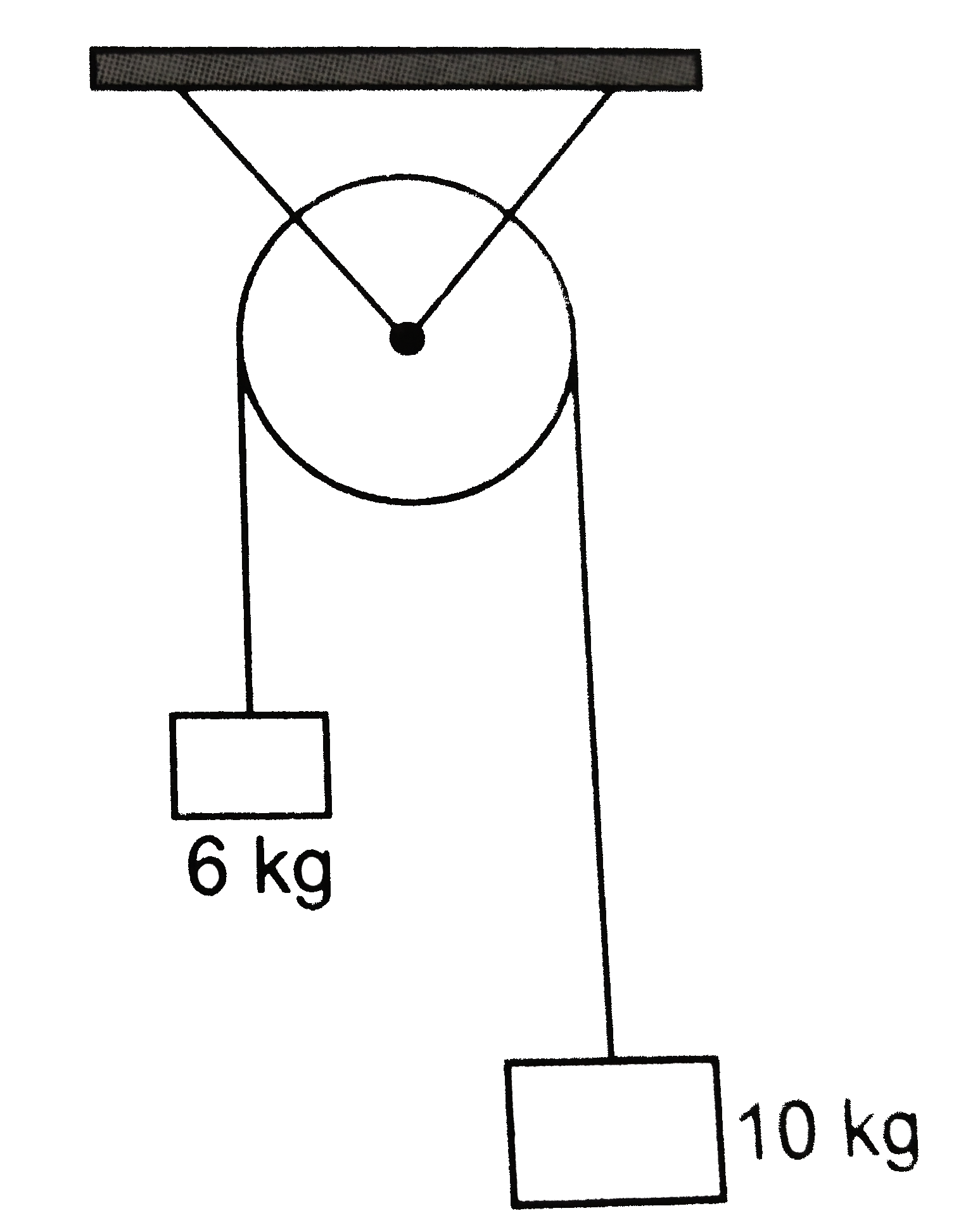 .A5.7NB7NC7.5ND73.5N
.A5.7NB7NC7.5ND73.5N - Question 3 - Select One
Force of friction and tension in a string are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDWeal forces
Find the acceleration and tension in the string in the following cases . The pulley and string are massless.
(a)
(b) View Solution
View SolutionForce of friction and tension in a string are
View SolutionStudy in fig. and answer the following questions accordingly. Neglect all friction and masses of the pulleys.

What is the tension in the string?View SolutionIn the system shown in fig the pulley is frictionless and the string massless if m1=m2 thrust on the pulley will be:
 View Solution
View SolutionConsider the system as shown in the figure. The pulley and the string are light and all the surfaces are frictionless. The tension in the string is (g=10m/s2) .
 View Solution
View Solution