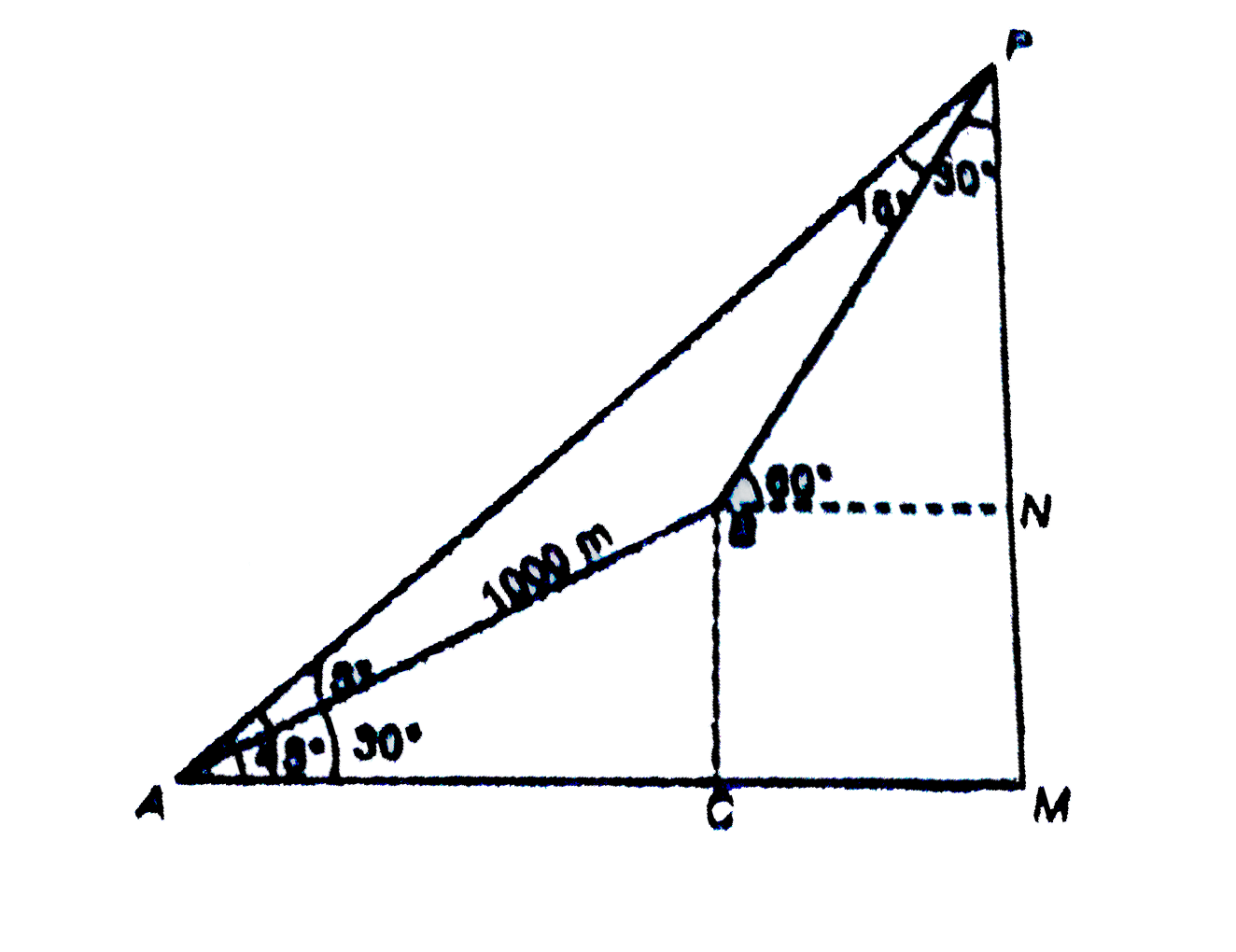
At the foot of a mountain, the elevation of its summit is 45∘. After ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. find the height of the mountain.
Let P be the top and M be the foot of the mountain PM.
Let the observer be at the observer ascends along the mountain at slope AB such that ∠MAB=30∘ and AB = 1000 m. Therefore, B is the second position of the observer, where the angle of elevation ∠NBP=60∘.
We have, ∠MAP=∠MPA=45∘,
∠MAB=30∘,∠NPB=30∘
Therefore, ∠BAP=∠=15∘
Hence, the triangleABP is iosceles and BP = AB = 1000 m (sides opposite to equal angles are equal)
Now, PM−PN+NM=PN+BC
=BPsin60∘+ABsin30∘
=1000(√32)+1000(12)=500(√3+1)
Hence, the height of the tower is 500(√3+1)m.
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Exercise
32 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)
5 Videos
- REAL NUMBERSBOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions
5 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
Similar Questions
At the foot of a mountain, the elevation of its summit is 45∘. After ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of its summit is 45∘, after ascending 1000m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ Find the height of the mountain.
View Solution
Knowledge Check
At the foot of the mountain, the elevation of its summit is 45∘ , after ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ . The height of the mountain is
A√3+12mB√3−12mC√3+12√3Dnone of theseAt the foot of the mountain the elevation of its summit is 45∘, after ascending 100 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. The height of the mountain is
A√3+12mB√3−13 mC√3+12√3 mDnone of theseAt the foot of a mountain the elevation of its summit is 45∘. After ascending 2000 meter towards the mountain upon an incline of 30∘, the elevation changes to 60∘. What is the height of the mountain.
A2000(√3−1) meterB1000(√3−1) meterC2000(√3+1) meterD1000(√3+1) meter
At the foot of a mountain the elevation of its summit is 450; after ascending 1000 m towards the mountain up a slope of 300 inclination, the elevation is fund to be 600 . Find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of its summit is 45∘. After ascending 600 meter towards the mountain, upon an incline of 30∘, the elevation changes to 60∘. Find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of it's peak is found to be(π4) ,after ascending 'h' meters toward the mountain up a slope of π6 inclination,the elevation is found to be π3 .Height of the mountain is
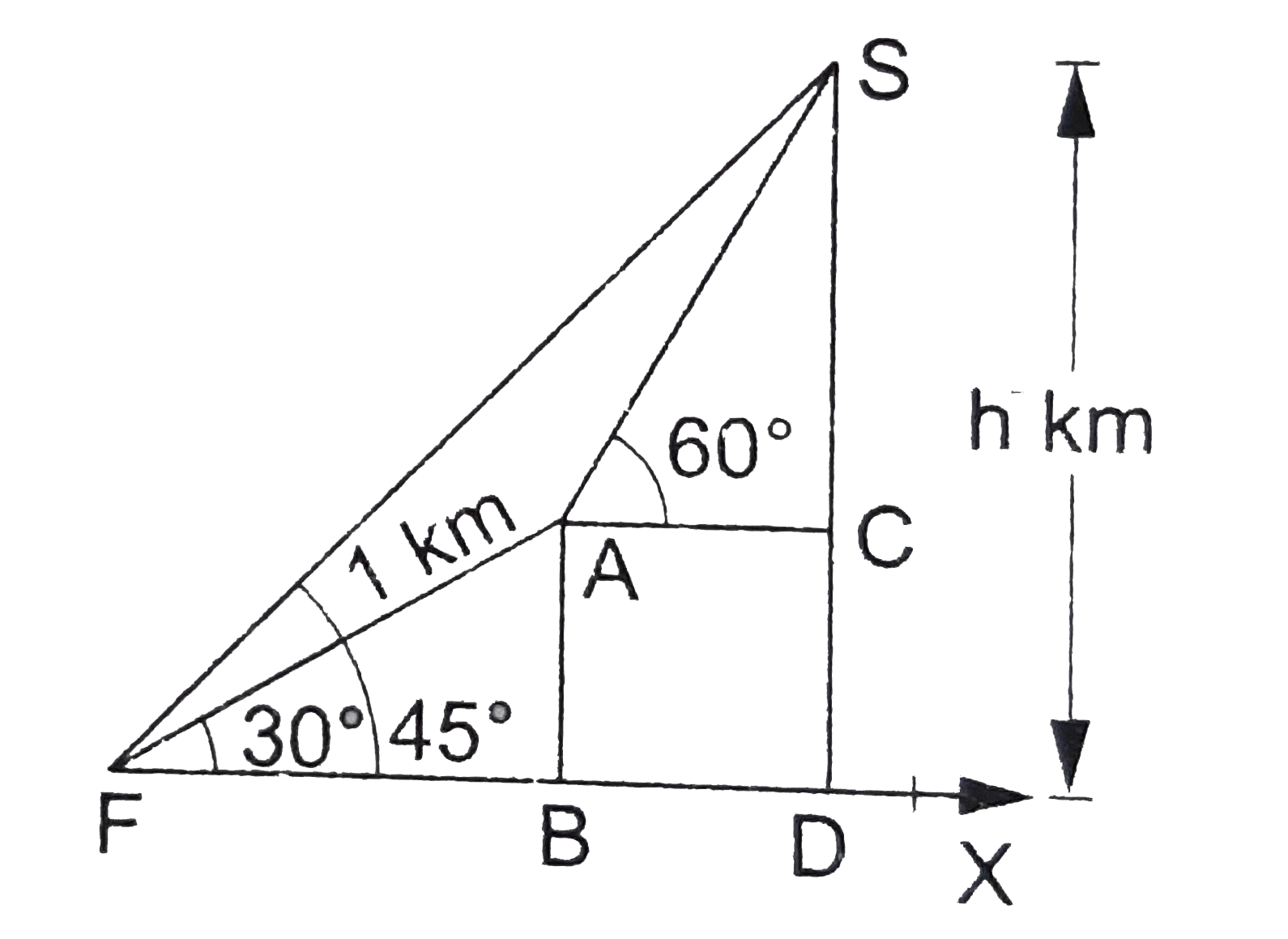
View SolutionAt the foot of a mountain, the angle of elevation of its summit is 45∘. After ascending 1 km towards the mountain up an incline of 30∘, the elevatioon changes to 60∘ (as shown in the given figure). Find the height of the mountain. [Given: √3=1.73.]
View SolutionAt the foot of a mountain, the elevation of its summit is 45∘. After ascending 2 km towards the mountain upon an incline of 30∘, the elevation changes to 60∘. The height of the mountain is
View Solution
