A block is suspended by an ideal spring of force constant k. If the block is pulled down by applying a constant force F and if maximum displacement of the block from its initial position of rest is , then
Increase in potential energy of the spring is
Let mass of the block hanging from the spring be m. Then initial elongation of the spring will be equal to mg/K. When the force F is applied to pull the block down, then work done by F & further loss of gravitational potential energy of the block is used to increase the potential energy of this spring.
From this equation , .
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE
1 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-I)
7 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS (SUBJECTIVE )
8 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
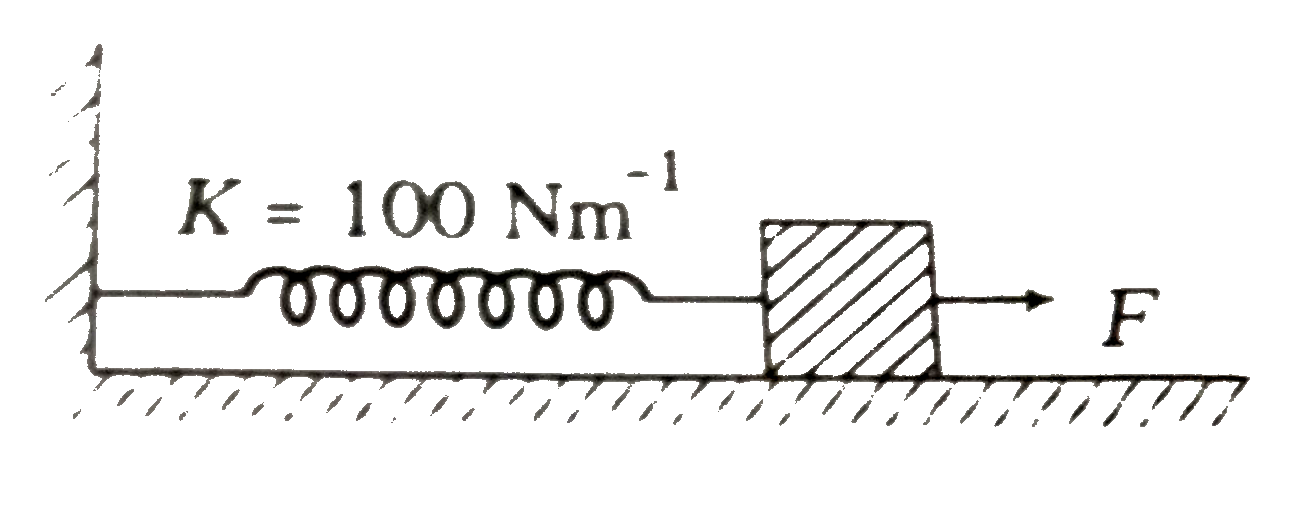
Consider a block connected to a light spring of spring constant 100Nm−1. Now the block is displaced by applying a constant force F which gives zero resultant force when spring is stretched through 10 cm.
Evaluate
(i) Work done by the spring force when the block attains equilibrium.
(ii) Net work done on the block when it attains maximum speed.
View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View Solution
Knowledge Check
A block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
Aincrease in energy stored in spring is kx20Bx0=3F2kCx0=2FkDwork done by applied force F is Fx0A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4Two blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
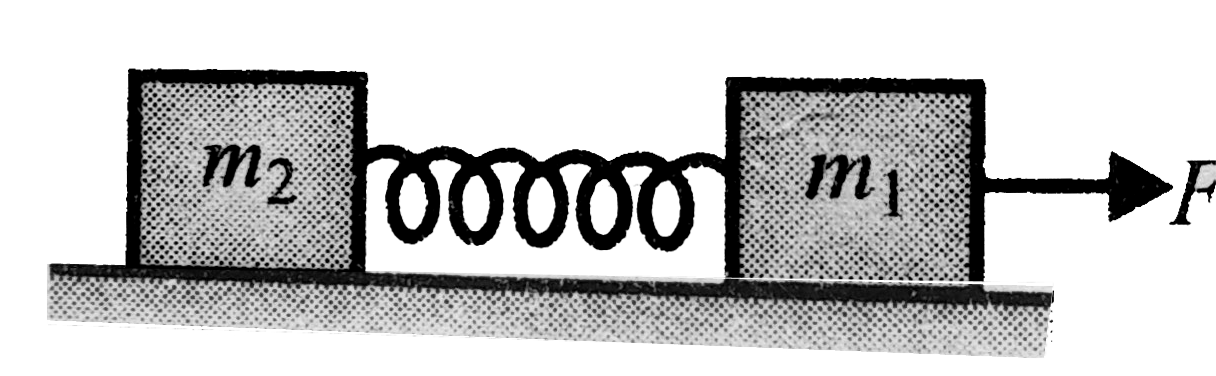
What is maximum elongation of spring.A2m1F(m1+m2)kBm21F2(m1+m2)kC2m2Fk(m1+m2)Dm22F2(m1+m2)2k
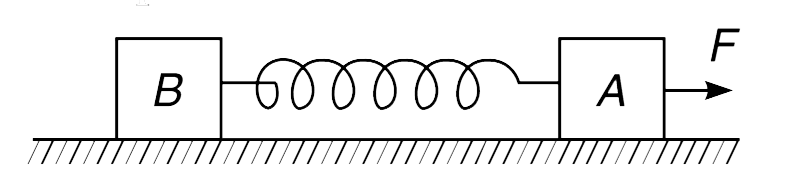
Two blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
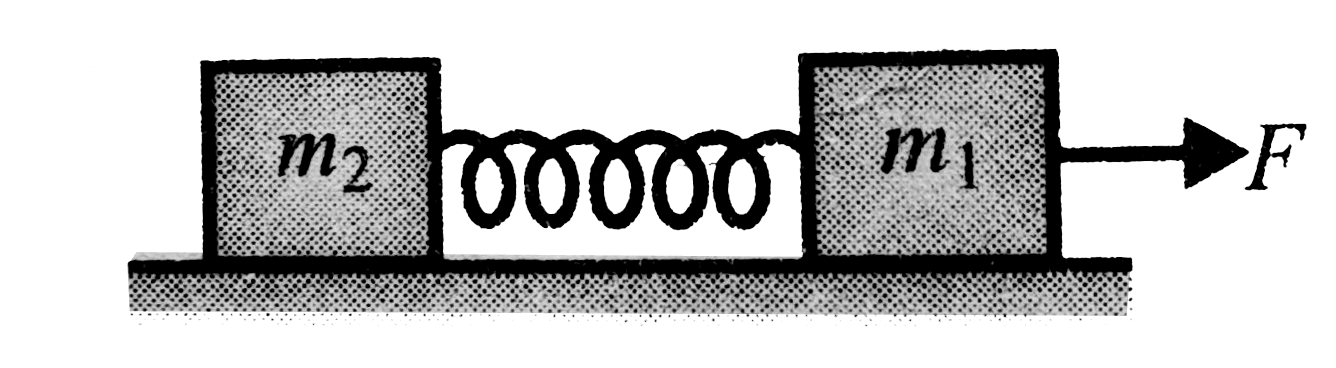
Which of the following statement is not true tn the watt of above system.
View SolutionTwo blocks of mass m and 2m are kept on a smooth horizontal surface. Theya are connected by an ideal spring of force constant k. Initially the spring is unstretched. A constant force is applied to the heavier block in the direction shown in figure. Suppose at time t displacement of smaller block is x1 then displacement of the heavier block at this moment would be
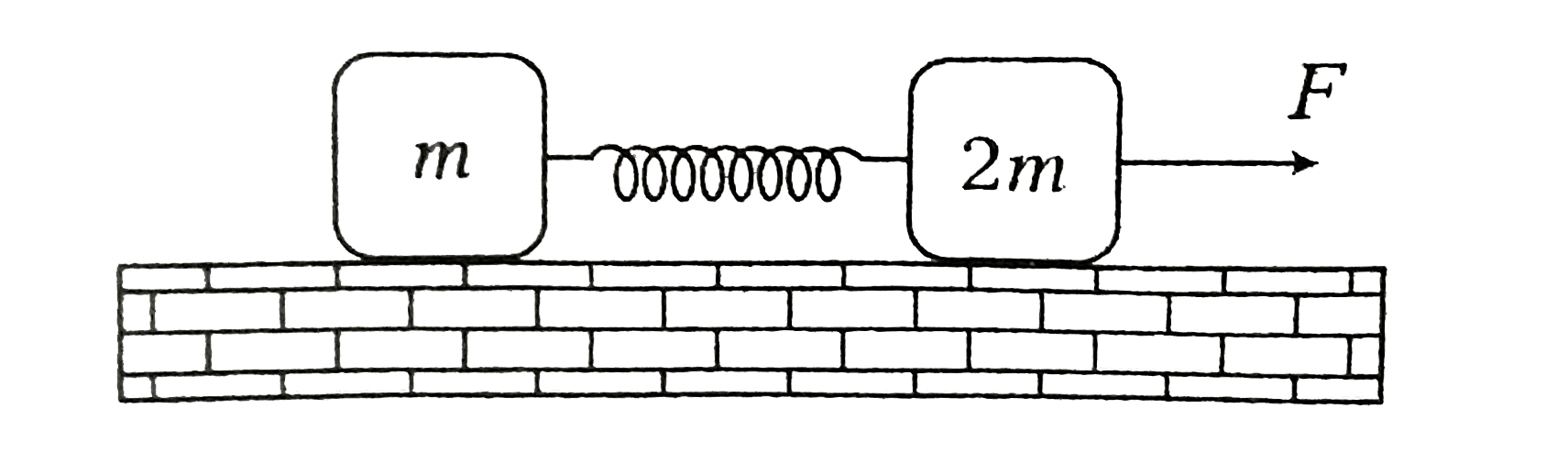
View SolutionA block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg/k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg/k
View Solution
