A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
average force acting on the ball is 2mvΔt
average force acting on the ball is mvΔt
kinetic energy of the ball becomes twice
kinetic energy of the ball remains same
The correct Answer is:A, D
Δ→P=−m→v−(m→v)=−2m→v
→F=Δ→PΔt=−2m→vΔt
F=2mv(Δt)
K.E.=12m(−v)2=12mv2
∴ (A) & (D)
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE1videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-I)7videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS (SUBJECTIVE )8videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
Similar Questions
A ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
 View Solution
View SolutionA ball of mass 5 kg moving velocity 3m/s impinges direction on another ball of mass 2 kg moving with velocity 0.5m/s towards the first ball. Find the velocity after impact, if e=47
View Solution
Knowledge Check
- Question 1 - Select One or More
A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
AThe average elastic force acting on the ball is m(u+v)ΔtBThe average elastic force acting on the ball is 2m(u+v)ΔtCthe kinetic energy of the ball increases by 2mu (u + v)Dthe kinetic energy of the ball does not change - Question 2 - Select One
A wall moving with velocity 2cms−1 towards the ball and ball is moving towards the wall with a velocity 10cms−1. It hits the wall normally and makes elastic collision with wall. The velocity of ball after collision with wall in cms−1.
A12B8C14D16 - Question 3 - Select One
A Sphere moving with velocity v strikes a wall moving towards the sphere with a velocity u. If the mass of the wall is infinitely large the work done by the wall during collision will be:
Amu(v+u)B2mu(v+u)C2mv(v+u)D2m(v+u)
A ball A moving with velocity u, impinges directly on an equal ball B moving with velocity v in the opposite direction. If the coefficient of elasticity is e and after impact ball A comes to rest, then uv=1+e1−e.
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA ball of mass m moving with velocity u impinges on a ball of mass em moving with velocity eu in the opposite direction. If the impact be direct and e be the coefficient of restitution then the velocity of the second ball after impact is the same as that of the first ball before impact.
View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.
 View Solution
View SolutionA ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :
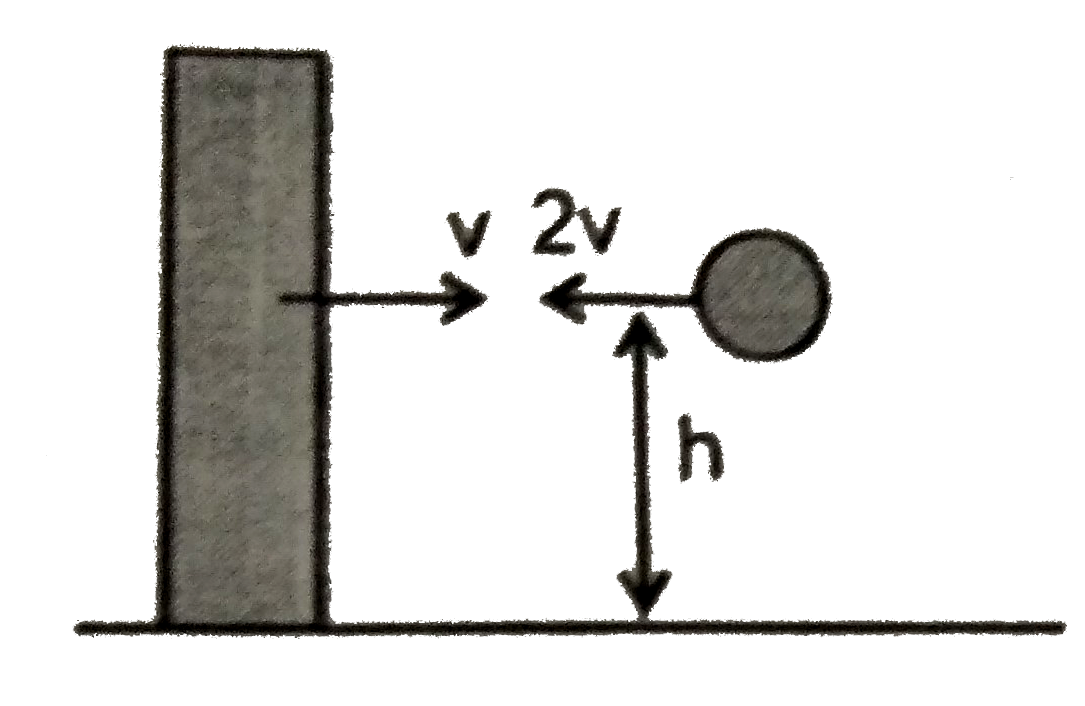 View Solution
View Solution

