A particle moves along between the points (0, -1) m and (0, 1) m under the influence of a force . Then,
the particle is moving along a semi-ellipse
the particle is moving along a semicircle
work done on the particle by by J
work done on the particle by is J
The correct Answer is:B, C
To solve the problem step by step, we need to calculate the work done by the force →F=(y2^i+x2^j) as the particle moves along the path defined by y=√1−x2 from the point (0, -1) to (0, 1).
Step 1: Understand the Path of the Particle
The equation y=√1−x2 describes the upper half of a circle with radius 1 centered at the origin. The particle moves from (0, -1) to (0, 1), which means it traces out a semicircular path.
Step 2: Set Up the Work Done Integral
The work done W by a force along a path can be calculated using the line integral:
W=∫C→F⋅d→s
where d→s=dx^i+dy^j.
Step 3: Express the Force in Terms of x
Since the path is defined by y=√1−x2, we can express F in terms of x:
→F=(y2^i+x2^j)=((√1−x2)2^i+x2^j)=(1−x2)^i+x2^j
Step 4: Calculate dy
To find dy in terms of dx, we differentiate y:
y=√1−x2⟹dy=−x√1−x2dx
Step 5: Substitute dy into the Work Integral
Now we substitute dy into the work integral:
W=∫1−1((1−x2)^i+x2^j)⋅(dx^i+dy^j)
This gives us:
W=∫1−1((1−x2)dx+x2dy)
Step 6: Substitute dy into the Integral
Substituting dy:
W=∫1−1((1−x2)dx+x2(−x√1−x2dx))
This simplifies to:
W=∫1−1((1−x2)−x3√1−x2)dx
Step 7: Evaluate the Integral
Now we can evaluate the integral:
1. The first part:
∫1−1(1−x2)dx=(x−x33)1−1=(1−13)−(−1+13)=23+23=43
2. The second part:
∫1−1−x3√1−x2dx=0(since it's an odd function over a symmetric interval)
Step 8: Combine Results
Thus, the total work done is:
W=43+0=43 Joules
Final Answer
The work done on the particle by the force →F as it moves along the semicircular path is:
43 Joules
The equation y=√1−x2 describes the upper half of a circle with radius 1 centered at the origin. The particle moves from (0, -1) to (0, 1), which means it traces out a semicircular path.
The work done W by a force along a path can be calculated using the line integral:
W=∫C→F⋅d→s
where d→s=dx^i+dy^j.
Since the path is defined by y=√1−x2, we can express F in terms of x:
→F=(y2^i+x2^j)=((√1−x2)2^i+x2^j)=(1−x2)^i+x2^j
To find dy in terms of dx, we differentiate y:
y=√1−x2⟹dy=−x√1−x2dx
Now we substitute dy into the work integral:
W=∫1−1((1−x2)^i+x2^j)⋅(dx^i+dy^j)
This gives us:
W=∫1−1((1−x2)dx+x2dy)
Substituting dy:
W=∫1−1((1−x2)dx+x2(−x√1−x2dx))
This simplifies to:
W=∫1−1((1−x2)−x3√1−x2)dx
Now we can evaluate the integral:
1. The first part:
∫1−1(1−x2)dx=(x−x33)1−1=(1−13)−(−1+13)=23+23=43
2. The second part:
∫1−1−x3√1−x2dx=0(since it's an odd function over a symmetric interval)
Thus, the total work done is:
W=43+0=43 Joules
The work done on the particle by the force →F as it moves along the semicircular path is:
43 Joules
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE
1 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-I)
7 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS (SUBJECTIVE )
8 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
STATEMENT-1: An elastic spring of force constant k is stretched by a small length x. The work done in extending the spring by a further length x is 2kx2.
because
STATEMENT-2: The work done in extending an elastic spring by a length x is proportional to x2.
View SolutionThree particles each of mass 'm' can slide on fixed frictionless circular track in the same horizontal plane as shown in the figure. Particle m1 moves with velocity v0 and hits particle m2, the coefficient of restitution being θ=1/2. AsSigmae m2 and m3 are initially in rest and lie along a radial line before impact and the spring is initially Unstretched. Then,
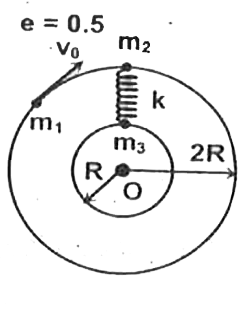
The velocity of m3 when extension in the spring is maximum
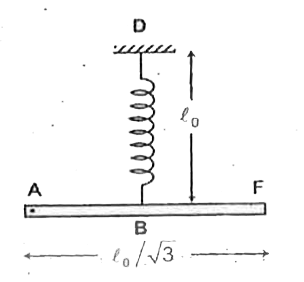
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View Solution
A particle of mass 3m is projected from point-A with speed 3v0 as shown in figure. When the particle is at point P, it explodes in three identical particles choose the INCORRECT statement regarding the physical quantities just before and just after explosion
View SolutionA body of mass 1 kg begins to move under the action of a time dependent force vec F = (2 t hat I + 3 t^(2) hat j) N , where hat i and hat j are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
View SolutionAn alpha particle moving with a velocity vec(v)_(1)=2hat(i)m//s is a uniform magnetic field experiences a force vec(F)_(1)=-4e(hat(j)-hat(k))N . When the particle moves with a velocity vec(v)_(2)=hat(j)m//s , then the force experienced by it is vec(F)_(2)=2e(hat(i)-hat(k))N . The magnetic induction vec(B) at that point is :
View SolutionA force acting on a certain particle depends of the particles position in the xy-plane. This force F is given by the expression
→F=(xyˆi+xyˆj)(1N/m2)
where x and y are expressed in metre. If →F is a conservation force ?
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View SolutionForce acting on particle is given by →F=2xyzˆi+x2xˆj+x2yˆk. Report the amount of work done in joule in displacing a particle of mass 2 kg from (0, 0, 0) to (1, 2, 3), acted upon by the given force.
View SolutionAn object is displaced from position vector →r1=(2ˆi+3ˆj)mto→r2=(4ˆi+6ˆj)m under a force →F=(3x2ˆi+2yˆj)N. Find the work done by this force.
View Solution1 kg द्रव्यमान का कोई पिण्ड किसी कालाश्रित बल →F=(2tˆi+3t2ˆj)N यहाँ ˆiऔर ˆj x और y अक्ष के अनुदिश मात्रक सदिश है के अधीन गति आरम्भ करता है तो समय t पर इस बल द्वारा विकसित शक्ति क्या होगी
View SolutionA particle moves along y=√1−x2 between the points (0,-1)m and (0,1)m under the influence of a force →F=(y2i+x2j)N.
Work done on the particle by the force →F is
View SolutionA particle moves along y=√1−x2 between the points (0,-1)m and (0,1)m under the influence of a force →F=(y2i+x2j)N.
Below which path particle moving
View SolutionA body of mass 1 kg begins to move under the action of a dependent force vec(F)=(2t hat(i)+3t^(2)hat(j))N where hat(i) and hat(j) are unit vectors along x and y axis. What power will be developed by the force at the time t ?
View SolutionAn object has a displacement from position vector →r1=(2ˆi+3ˆj)m to →r2=(4ˆi+6ˆj)m under a force →F=(3x2ˆi+2yˆj)N. Find the work done by this force.
View SolutionUnder influence of a force vec(F) (x) = (3x^(2) - 2x +5) hat(i) N , there is displacement of a particle from x = 0 and x = 5 m on X - axis .So work done is ………. J .
View Solution
