A ring of mass m having velocity v0 is placed on a long plank lies on smooth horizontal surface at time t=0 as shown. Find the time when the ring start pure rolling on the plank. [μ is coefficient of friction between the ring and the plank.]
![A ring of mass m having velocity v(0) is placed on a long plank lies on smooth horizontal surface at time t=0 as shown. Find the time when the ring start pure rolling on the plank. [mu is coefficient of friction between the ring and the plank.]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_XI_RT_P2_E01_470_Q01.png)
v0μg
v04μg
v03μg
2v05μg
v−ωR=v
[v0−(μmgm)r]−μmg×R(mR2)×t×R
=μmgm×t
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A plank of mass M is moving on a smooth horizontal surface with speed 'v0'. At t=0 a sphere of mass 'm' and radius 'r' is gently placed on it and simultaneously a constant horizontal force 'F' is applied on the plank in the opposite direction of v0. Find the time at which sphere starts rolling on the plank. The coefficient of friction between the plank and the sphere is μ.

View SolutionA nonconducting ring (of mass m, radius r, having charge Q) is placed on a rough horizontal surface (in a cylindrical region with transverse magnetic field). The field is increasing with time at the rate R and coefficient of friction between the surface and the ring is μ. For ring to remain in equilibrium μ should be greater than equal to,
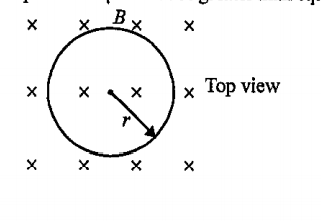
View Solution
Knowledge Check
A uniform ring placed on a rough horizontal surface is given a sharp impulse as shown in the figure-5.130. As a consequence, it acquires a linear velocity of 2m/s. If coefficient of friction between the ring and the horizontal surface is 0.4 :
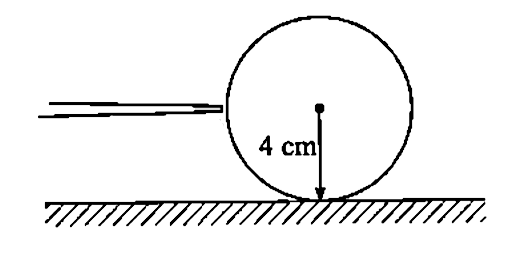 ARing wil lstart pure rolling afler O.25sBWhen ring will start pure rolling its .velocity is 1m//sCAfter 0.5s from impulse its velocity is 1m//s.DAfter0.125 s from impulse its velocity is 1m//s.
ARing wil lstart pure rolling afler O.25sBWhen ring will start pure rolling its .velocity is 1m//sCAfter 0.5s from impulse its velocity is 1m//s.DAfter0.125 s from impulse its velocity is 1m//s.A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB2ω20r227μgC4ω20r281μgD2ω20r281μgA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
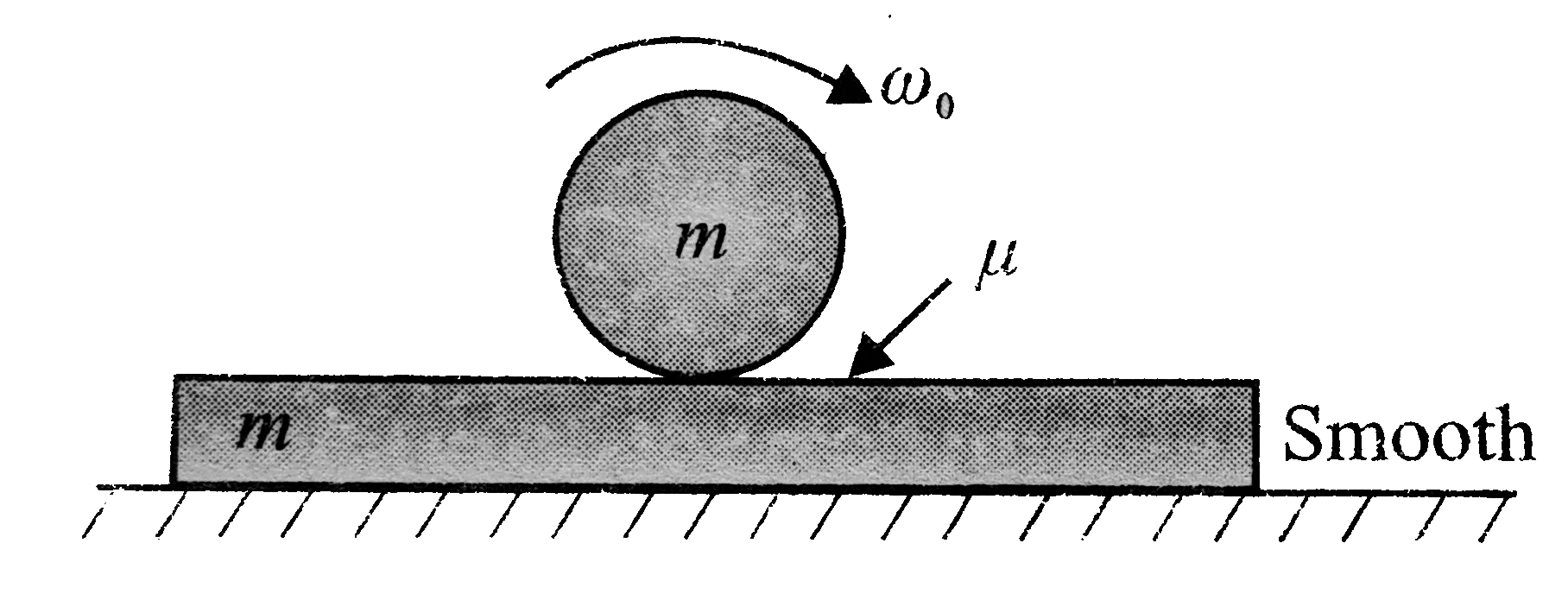
Find the time t at which the pure roiling startsAω0r9μgB2ω0r9μgCω0r3μgD2ω0rμg
A plank of mass M and length L is placed at rest on a smooth horizontal surface A small block of mass m is projected wii:h a velocity v0 as shown in the Fig. 3.31 (a), The coefficient of friction between the block and the plank is μ, plank is very long so that block eventually comes to rest on it.
(i) Find the work done by the ftjctioh force on the block during the period it slides on the plank. Is the Work positive or negative ?'
(ii) Calculate the work done on the plank during the same period. Is the work positive or negative?
(iii) Also, determine the net work done by friction. Is it positive or negative ?

View SolutionA plank of mass M rests on a smooth horizontal plane. A sphere of mass m and radius r is placed on the rough upper surface of the plank and the plank is suddenly given a velocity v in the direction of its length. Find the time after which the sphere begins pure rolling, if the coefficient of friction between the plank and the sphere is μ and the plank is sufficiently long.
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View SolutionA plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling starts
View Solution
