Calculate the coefficient of correlation between the values of x and y given below:
To calculate the coefficient of correlation between the values of x and y, we will follow these steps:
Step 1: Gather the Data
We have the following values for x and y:
- x={−10,−5,0,5,10}
- y={5,9,7,11,13}
Step 2: Calculate x2, y2, and xy
We will calculate x2, y2, and xy for each pair of x and y:
| x | y | x2 | y2 | xy |
|----------|---------|------------|------------|------------|
| -10 | 5 | 100 | 25 | -50 |
| -5 | 9 | 25 | 81 | -45 |
| 0 | 7 | 0 | 49 | 0 |
| 5 | 11 | 25 | 121 | 55 |
| 10 | 13 | 100 | 169 | 130 |
Step 3: Calculate the Summations
Now we will calculate the necessary summations:
- Σx=−10−5+0+5+10=0
- Σy=5+9+7+11+13=45
- Σx2=100+25+0+25+100=250
- Σy2=25+81+49+121+169=445
- Σxy=−50−45+0+55+130=90
Step 4: Plug Values into the Correlation Formula
The formula for the coefficient of correlation r is given by:
r=nΣxy−ΣxΣy√(nΣx2−(Σx)2)(nΣy2−(Σy)2)
Where n is the number of observations. Here, n=5.
Substituting the values we calculated:
r=5⋅90−0⋅45√(5⋅250−02)(5⋅445−452)
Step 5: Simplify the Numerator
Calculating the numerator:
5⋅90−0⋅45=450−0=450
Step 6: Simplify the Denominator
Calculating the denominator:
1. nΣx2−(Σx)2=5⋅250−02=1250−0=1250
2. nΣy2−(Σy)2=5⋅445−452=2225−2025=200
Now, substituting these values into the denominator:
√(1250)(200)=√250000=500
Step 7: Final Calculation
Now we can calculate r:
r=450500=0.9
Conclusion
The coefficient of correlation r is 0.9.
---
We have the following values for x and y:
- x={−10,−5,0,5,10}
- y={5,9,7,11,13}
We will calculate x2, y2, and xy for each pair of x and y:
|----------|---------|------------|------------|------------|
| -10 | 5 | 100 | 25 | -50 |
| -5 | 9 | 25 | 81 | -45 |
| 0 | 7 | 0 | 49 | 0 |
| 5 | 11 | 25 | 121 | 55 |
| 10 | 13 | 100 | 169 | 130 |
Now we will calculate the necessary summations:
- Σx=−10−5+0+5+10=0
- Σy=5+9+7+11+13=45
- Σx2=100+25+0+25+100=250
- Σy2=25+81+49+121+169=445
- Σxy=−50−45+0+55+130=90
The formula for the coefficient of correlation r is given by:
Calculating the numerator:
Calculating the denominator:
2. nΣy2−(Σy)2=5⋅445−452=2225−2025=200
Now we can calculate r:
The coefficient of correlation r is 0.9.
Topper's Solved these Questions
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Solved Problems(Objective)
24 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Exercise 1
5 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Comprehension Type
6 Videos
- SET, RELATION & FUNCTIONBOOK - FIITJEECHAPTER - SET, RELATION & FUNCTIONEXERCISE - Exercise 3
8 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - NUMERICAL BASED
4 Videos
Similar Questions
Knowledge Check
Distance between the lines 5x+3y-7=0 and 15x+9y+14=0 is
A35√34B13√34C353√34D352√34Find the value of x and y in the given equation 57x×y113=12:
A−2,9B9,2C4,3D9,4Find the value of x and y in the given equatyion 57x×y113=12:
A-2 , 9B9,2C4,3D9,4
Calculate Karl Pearson's coefficient of correlation between the values of X and Y for the following data:
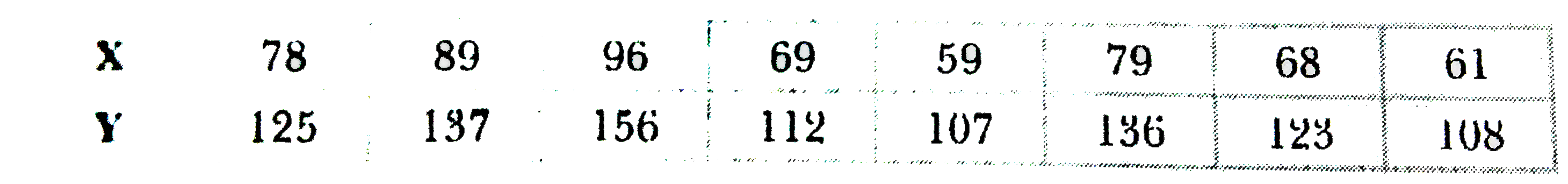
Assume 69 and 112 as the mean values for X and Y respectively.
View Solutiondistance between the lines 5x+3y−7=0 and 15x+9y+14=0
View SolutionThe coefficient of correlation between X and Y is 0.6. Their covariance is 4.8 var (x)=9. Find the value of σy.
View SolutionIf x[23]+y[−11]=[105], find the values of x and y.
View SolutionIf (x+y, 5) = (10, y-3), find the values of x and y.
View Solution


