In a partially destroyed laboratory record of an analysis correlation data, the following results only are legible: variance of x=9, regression equations 8x-10y+66=0, 40x-18y=214.
What are (a) the mean values of x and y, (b) the standard deviation of y and (c) the coefficient of correlation between x and y?
To solve the given problem, we will follow these steps:
Given Data
- Variance of x = 9
- Regression equations:
1. 8x−10y+66=0
2. 40x−18y=214
Step 1: Find the Mean Values of x and y
The mean values ¯x and ¯y can be found by solving the two regression equations simultaneously.
Rewrite the equations:
1. From 8x−10y+66=0:
10y=8x+66⟹y=810x+6610⟹y=0.8x+6.6
2. From 40x−18y=214:
18y=40x−214⟹y=4018x−21418⟹y=209x−1079
Set the two equations for y equal to each other:
0.8x+6.6=209x−1079
Clear the fractions by multiplying through by 9:
9(0.8x)+9(6.6)=20x−107
7.2x+59.4=20x−107
Rearranging gives:
20x−7.2x=59.4+107
12.8x=166.4⟹x=166.412.8=13
Substituting x back to find y:
y=0.8(13)+6.6=10.4+6.6=17
Thus, the mean values are:
- ¯x=13
- ¯y=17
Step 2: Find the Standard Deviation of y
Using the formula:
σy=byx⋅σxr
Where:
- σx=√Variance of x=√9=3
- byx is the slope of the regression of y on x from the first regression equation, which is 0.8.
- r is the correlation coefficient we will find in the next step.
Step 3: Find the Coefficient of Correlation r
From the regression equations:
- byx=0.8
- bxy=1840=0.45
Using the relationship:
r=√byx⋅bxy=√0.8⋅0.45
r=√0.36=0.6
Step 4: Calculate Standard Deviation of y
Now substituting the values into the formula for σy:
σy=0.8⋅30.6=2.40.6=4
Final Answers
- (a) Mean values: ¯x=13, ¯y=17
- (b) Standard deviation of y: σy=4
- (c) Coefficient of correlation r=0.6
- Variance of x = 9
- Regression equations:
1. 8x−10y+66=0
2. 40x−18y=214
1. From 8x−10y+66=0:
10y=8x+66⟹y=810x+6610⟹y=0.8x+6.6
18y=40x−214⟹y=4018x−21418⟹y=209x−1079
0.8x+6.6=209x−1079
9(0.8x)+9(6.6)=20x−107
7.2x+59.4=20x−107
20x−7.2x=59.4+107
12.8x=166.4⟹x=166.412.8=13
y=0.8(13)+6.6=10.4+6.6=17
- ¯x=13
- ¯y=17
σy=byx⋅σxr
- σx=√Variance of x=√9=3
- byx is the slope of the regression of y on x from the first regression equation, which is 0.8.
- r is the correlation coefficient we will find in the next step.
- byx=0.8
- bxy=1840=0.45
r=√byx⋅bxy=√0.8⋅0.45
r=√0.36=0.6
σy=0.8⋅30.6=2.40.6=4
- (a) Mean values: ¯x=13, ¯y=17
- (b) Standard deviation of y: σy=4
- (c) Coefficient of correlation r=0.6
Topper's Solved these Questions
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Solved Problems(Objective)
24 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Exercise 1
5 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Comprehension Type
6 Videos
- SET, RELATION & FUNCTIONBOOK - FIITJEECHAPTER - SET, RELATION & FUNCTIONEXERCISE - Exercise 3
8 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - NUMERICAL BASED
4 Videos
Similar Questions
Calculate the coeficient of correlation between X and Y.
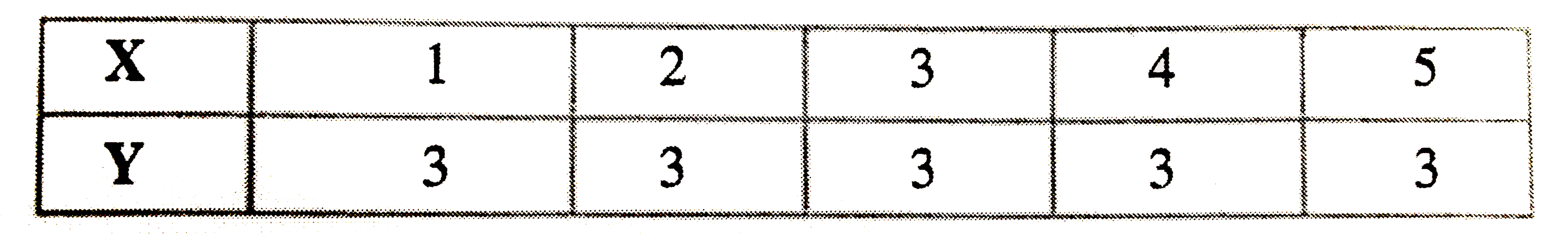
View SolutionIn a partially destroyed laboratory record of an analysis correlation data, the following results only are legible: variance of x=9, regression equations 8x-10y+66=0, 40x-18y=214.
What are (a) the mean values of x and y, (b) the standard deviation of y and (c) the coefficient of correlation between x and y?
View Solution
Knowledge Check
The two lines of regression are 8x−10y=66 and 40x−18y=214 and variance of x series is 9. What is the standard deviation of y series?
A3B4C6D8The variance of a data is 144, find the standard deviation
A3B4C6D9
Find out coefficient of rank correlation between X and Y

View SolutionCalculate coefficient of correlation between series X and Y.

View SolutionIf the regression equations are 8x–10y+66=0 and 40x–18y=214, the mean value of y is…..
View SolutionFrom the following information, determine coefficient of correlation between X and Y series.
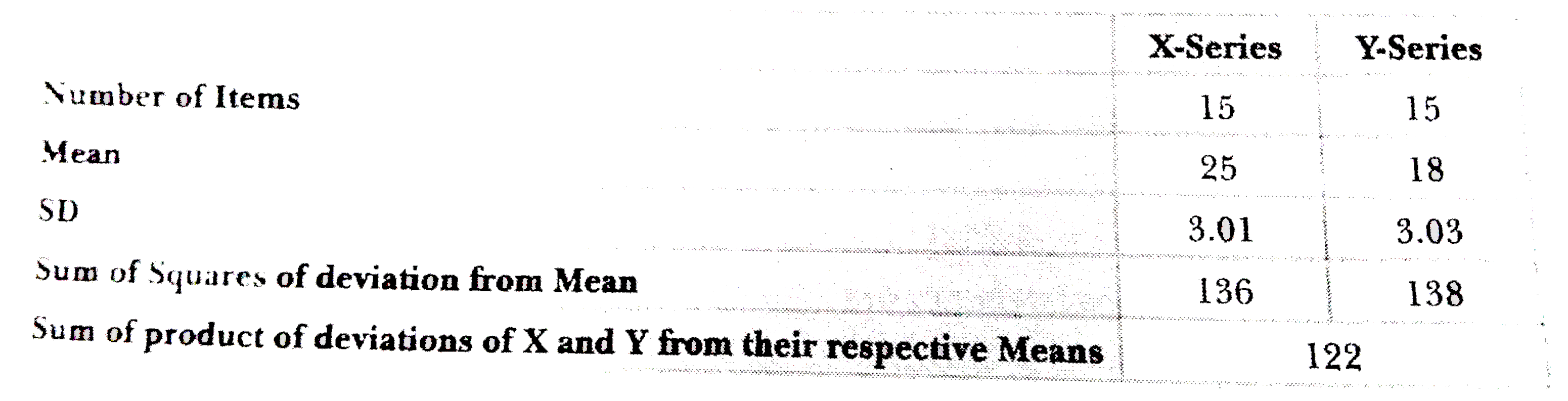
View SolutionFind the Kari Pearson's Coefficient of correlation between x and y for the data

View SolutionIf the two lines of regression are 3x+2y=26and6x+y=31, then the coefficient of correlation between x and y is ……………..
View Solution
