Calculate the rank correlation coefficient from the data given below:
Marks in Statistics45563954554058603036Marks in Mathematics40363044383245422034
To calculate the rank correlation coefficient from the given data, we will follow these steps:
Step 1: Organize the Data
We have two sets of marks:
- Marks in Statistics (X): 45, 56, 39, 54, 55, 40, 58, 60, 30, 36
- Marks in Mathematics (Y): 40, 36, 30, 44, 38, 32, 45, 42, 20, 34
Step 2: Assign Ranks
We will rank the marks in each subject. The highest mark gets the rank of 1, the second highest gets 2, and so on. If there are ties, we assign the average rank to the tied values.
Ranks for Statistics (X):
- 60 → 1
- 58 → 2
- 56 → 3
- 55 → 4
- 54 → 5
- 45 → 6
- 40 → 7
- 39 → 8
- 36 → 9
- 30 → 10
Ranks for Mathematics (Y):
- 45 → 1
- 44 → 2
- 42 → 3
- 40 → 4
- 38 → 5
- 36 → 6
- 34 → 7
- 32 → 8
- 30 → 9
- 20 → 10
Step 3: Calculate the Difference in Ranks
Now we will calculate the difference (d) between the ranks of X and Y for each student.
| X (Marks) | Rank X | Y (Marks) | Rank Y | d (Rank X - Rank Y) |
|-----------|--------|-----------|--------|---------------------|
| 45 | 6 | 40 | 4 | 2 |
| 56 | 3 | 36 | 6 | -3 |
| 39 | 8 | 30 | 9 | -1 |
| 54 | 5 | 44 | 2 | 3 |
| 55 | 4 | 38 | 5 | -1 |
| 40 | 7 | 32 | 8 | -1 |
| 58 | 2 | 45 | 1 | 1 |
| 60 | 1 | 42 | 3 | -2 |
| 30 | 10 | 20 | 10 | 0 |
| 36 | 9 | 34 | 7 | 2 |
Step 4: Calculate d²
Now we will square the differences (d²).
| d | d² |
|---|-----|
| 2 | 4 |
| -3| 9 |
| -1| 1 |
| 3 | 9 |
| -1| 1 |
| -1| 1 |
| 1 | 1 |
| -2| 4 |
| 0 | 0 |
| 2 | 4 |
Step 5: Summation of d²
Now we will sum up the squared differences.
∑d2=4+9+1+9+1+1+1+4+0+4=34
Step 6: Calculate the Rank Correlation Coefficient
Using the formula for the rank correlation coefficient rs:
rs=1−6∑d2n(n2−1)
Where:
- n = number of pairs (here n=10)
- ∑d2=34
Substituting the values:
rs=1−6×3410(102−1)=1−20410×99=1−204990
Calculating:
rs=1−0.206=0.794
Final Answer
The rank correlation coefficient is rs=0.794.
We have two sets of marks:
- Marks in Statistics (X): 45, 56, 39, 54, 55, 40, 58, 60, 30, 36
- Marks in Mathematics (Y): 40, 36, 30, 44, 38, 32, 45, 42, 20, 34
We will rank the marks in each subject. The highest mark gets the rank of 1, the second highest gets 2, and so on. If there are ties, we assign the average rank to the tied values.
- 60 → 1
- 58 → 2
- 56 → 3
- 55 → 4
- 54 → 5
- 45 → 6
- 40 → 7
- 39 → 8
- 36 → 9
- 30 → 10
- 45 → 1
- 44 → 2
- 42 → 3
- 40 → 4
- 38 → 5
- 36 → 6
- 34 → 7
- 32 → 8
- 30 → 9
- 20 → 10
Now we will calculate the difference (d) between the ranks of X and Y for each student.
|-----------|--------|-----------|--------|---------------------|
| 45 | 6 | 40 | 4 | 2 |
| 56 | 3 | 36 | 6 | -3 |
| 39 | 8 | 30 | 9 | -1 |
| 54 | 5 | 44 | 2 | 3 |
| 55 | 4 | 38 | 5 | -1 |
| 40 | 7 | 32 | 8 | -1 |
| 58 | 2 | 45 | 1 | 1 |
| 60 | 1 | 42 | 3 | -2 |
| 30 | 10 | 20 | 10 | 0 |
| 36 | 9 | 34 | 7 | 2 |
Now we will square the differences (d²).
|---|-----|
| 2 | 4 |
| -3| 9 |
| -1| 1 |
| 3 | 9 |
| -1| 1 |
| -1| 1 |
| 1 | 1 |
| -2| 4 |
| 0 | 0 |
| 2 | 4 |
Now we will sum up the squared differences.
Using the formula for the rank correlation coefficient rs:
- n = number of pairs (here n=10)
- ∑d2=34
The rank correlation coefficient is rs=0.794.
Topper's Solved these Questions
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Solved Problems(Objective)
24 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Exercise 1
5 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Comprehension Type
6 Videos
- SET, RELATION & FUNCTIONBOOK - FIITJEECHAPTER - SET, RELATION & FUNCTIONEXERCISE - Exercise 3
8 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - NUMERICAL BASED
4 Videos
Similar Questions
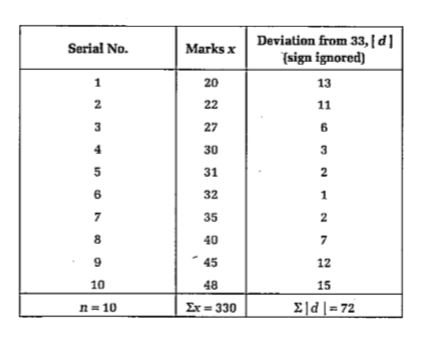
Calculate the mean deviation from the arithmatic mean of the following series of marks :
20,22,27,30,31,32,35,40,45,48
View SolutionFind the mean deviation about the median for the data given below.
45,36,50,60,53,46,51,48,72,42.
View SolutionCalculate the mean devation from the mean the following data:
Marks0−1010−2020−3030−4040−50No. of stu.5815166
View SolutionCalculate median , quartiles , 6th decile and 70 th percentile from the following data :
Marks (less than)8070605040302010Number of Students1009080603220135
View SolutionCaculate the median and mode from the following data :
Marks0−1010−2020−3030−4040−5050−6060−7070−80Number of Students 2 18 30 45 35 20 6 3
View SolutionFind out the range and coefficient of range from the following data:
6,12,30,24,45,52,40
View SolutionDistribution of marks obtained by 100 student of a class is given below . Find out the median marks
Marks051015202530354045Number of Students46155812281435
View SolutionCalculate the mean marks from the following data:
Marks20−2525−3030−3535−4040−4545−5050−55No. of Students 10 12 8 20 11 4 5
View SolutionCalculate the mean marks from the following data:
Marks20−2525−3030−3535−4040−4545−5050−55No. of Students 10 12 8 20 11 4 5
View SolutionCalculate the median from the following series :
Age (Years)55−6050−5545−5040−4535−4030−3525−3020−25Number of Students 7 13 10 15 30 33 28 14
View Solution
