Regression equation of yon is 8x-10y+66=0 σx=3. Hence cov(x,y) is equal to
11,25
7.2
2,4
None of these
The correct Answer is:B
To find the covariance of x and y given the regression equation of y on x and the standard deviation of x, we can follow these steps:
Step 1: Rewrite the Regression Equation
The given regression equation is:
8x−10y+66=0
Rearranging this equation to express y in terms of x:
10y=8x+66⟹y=810x+6610
Thus, we have:
y=0.8x+6.6
Here, the coefficient byx=0.8.
Step 2: Identify the Standard Deviation of x
We are given that the standard deviation of x is:
σx=3
The variance of x can be calculated as:
Variance(x)=σ2x=32=9
Step 3: Use the Relationship Between Covariance and Regression Coefficient
The relationship between the covariance of x and y and the regression coefficient is given by:
byx=Cov(x,y)Var(x)
Rearranging this formula to find the covariance:
Cov(x,y)=byx×Var(x)
Step 4: Substitute the Values
Now substituting the values we have:
Cov(x,y)=0.8×9=7.2
Conclusion
Thus, the covariance of x and y is:
Cov(x,y)=7.2
The given regression equation is:
8x−10y+66=0
Rearranging this equation to express y in terms of x:
10y=8x+66⟹y=810x+6610
Thus, we have:
y=0.8x+6.6
Here, the coefficient byx=0.8.
We are given that the standard deviation of x is:
σx=3
The variance of x can be calculated as:
Variance(x)=σ2x=32=9
The relationship between the covariance of x and y and the regression coefficient is given by:
byx=Cov(x,y)Var(x)
Rearranging this formula to find the covariance:
Cov(x,y)=byx×Var(x)
Now substituting the values we have:
Cov(x,y)=0.8×9=7.2
Thus, the covariance of x and y is:
Cov(x,y)=7.2
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Assignment Problems (Objective) Level II25videos
STATISTICS
- BOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Assertion -Reasoning Type MCQ Single Correct(Level II)2videos
STATISTICS
- BOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Assignment Problems (Subjective)14videos
STATISTICS
- BOOK - FIITJEECHAPTER - SET, RELATION & FUNCTIONEXERCISE - Exercise 38videos
SET, RELATION & FUNCTION
- BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - NUMERICAL BASED4videos
STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
In the regression equation of X on Y
AX is independent and Y is dependent.BY is independent and X is dependent.CBoth X and Y are independent.DBoth X and Y are dependent. - Question 2 - Select One
Regression equation of Y on X 2x+3y-12=0. The value of byx is
A−2/3B−3/2C2/3D3/2 - Question 3 - Select One
If the regression equation x on y is 3x+2y=26 then bxy equals to
A3/2B2/3C−3/2D−2/3
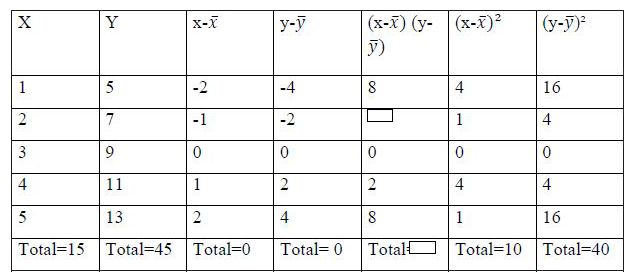
Mean of x=¯x=□
Mean y=¯y=□
bxy=□□
byx=□□
Regression equation of x on y is x−¯x=bxy(y−¯y)
∴ Regression equation of x on y is □
Regression equation of y on x is y−¯y=byx(x−¯x)
∴ Regression equation of y on x is □View SolutionIn a partially destroyed laboratory record of an analysis correlation data, the following results only are legible: variance of x=9, regression equations 8x-10y+66=0, 40x-18y=214.
What are (a) the mean values of x and y, (b) the standard deviation of y and (c) the coefficient of correlation between x and y?View Solution
bxy=□□
byx=□□
∴ Regression equation of x on y is □
∴ Regression equation of y on x is □View SolutionIf the regression equations are 8x–10y+66=0 and 40x–18y=214, the mean value of y is…..
View SolutionIn a partially destroyed laboratory record of an analysis correlation data, the following results only are legible: variance of x=9, regression equations 8x-10y+66=0, 40x-18y=214.
What are (a) the mean values of x and y, (b) the standard deviation of y and (c) the coefficient of correlation between x and y?View Solution

