A particle is having mass m & charge +q is projected horizontally from point O. Electric field is present and is directed vertically downward .


To solve the problem step by step, we need to analyze the motion of a charged particle projected horizontally in the presence of a vertical electric field.
Step 1: Understand the Initial Conditions
- A particle with mass m and charge +q is projected horizontally from point O with an initial velocity v.
- An electric field →E is directed vertically downward.
Step 2: Analyze Forces Acting on the Particle
- The only force acting on the particle in the vertical direction is due to the electric field. The force →F on the particle can be given by:
→F=q→E
- Since the electric field is downward, the force will also act downward.
Step 3: Determine the Acceleration
- The acceleration →a of the particle due to the electric force is given by:
→a=→Fm=q→Em
- This acceleration acts downward and can be denoted as ay=qEm.
Step 4: Analyze the Motion in the Horizontal Direction
- In the horizontal direction (x-direction), there is no force acting on the particle, so the horizontal motion is uniform:
x(t)=vt
- Here, v is the constant horizontal velocity.
Step 5: Analyze the Motion in the Vertical Direction
- The vertical motion is uniformly accelerated motion due to the downward acceleration ay:
y(t)=12ayt2=12(qEm)t2
Step 6: Eliminate Time to Find the Relationship Between y and x
- From the horizontal motion, we can express time t in terms of x:
t=xv
- Substitute this expression for t into the equation for y(t):
y=12(qEm)(xv)2
- This simplifies to:
y=qE2mv2x2
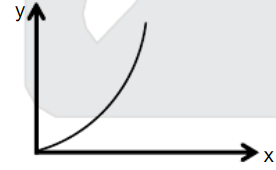
- This equation represents a parabolic relationship between y and x.
Step 7: Conclusion
- The trajectory of the particle in the y−x plane is a parabola that opens upwards (since the electric field is downward, the particle accelerates downward).
Final Graph
- The graph of y versus x will be a parabola, confirming that the particle follows a parabolic path.
- A particle with mass m and charge +q is projected horizontally from point O with an initial velocity v.
- An electric field →E is directed vertically downward.
- The only force acting on the particle in the vertical direction is due to the electric field. The force →F on the particle can be given by:
→F=q→E
- Since the electric field is downward, the force will also act downward.
- The acceleration →a of the particle due to the electric force is given by:
→a=→Fm=q→Em
- This acceleration acts downward and can be denoted as ay=qEm.
- In the horizontal direction (x-direction), there is no force acting on the particle, so the horizontal motion is uniform:
x(t)=vt
- Here, v is the constant horizontal velocity.
- The vertical motion is uniformly accelerated motion due to the downward acceleration ay:
y(t)=12ayt2=12(qEm)t2
- From the horizontal motion, we can express time t in terms of x:
t=xv
- Substitute this expression for t into the equation for y(t):
y=12(qEm)(xv)2
- This simplifies to:
y=qE2mv2x2
- This equation represents a parabolic relationship between y and x.
- The trajectory of the particle in the y−x plane is a parabola that opens upwards (since the electric field is downward, the particle accelerates downward).
- The graph of y versus x will be a parabola, confirming that the particle follows a parabolic path.
Topper's Solved these Questions
Similar Questions
A simple pendulum having caharge q1 mass ma and effective length 1, is suspended from a rigid support between the plates of charged horizontal capacitor. Electric field in the capacitor is perpendicular to the plates and directed vertically downwards .
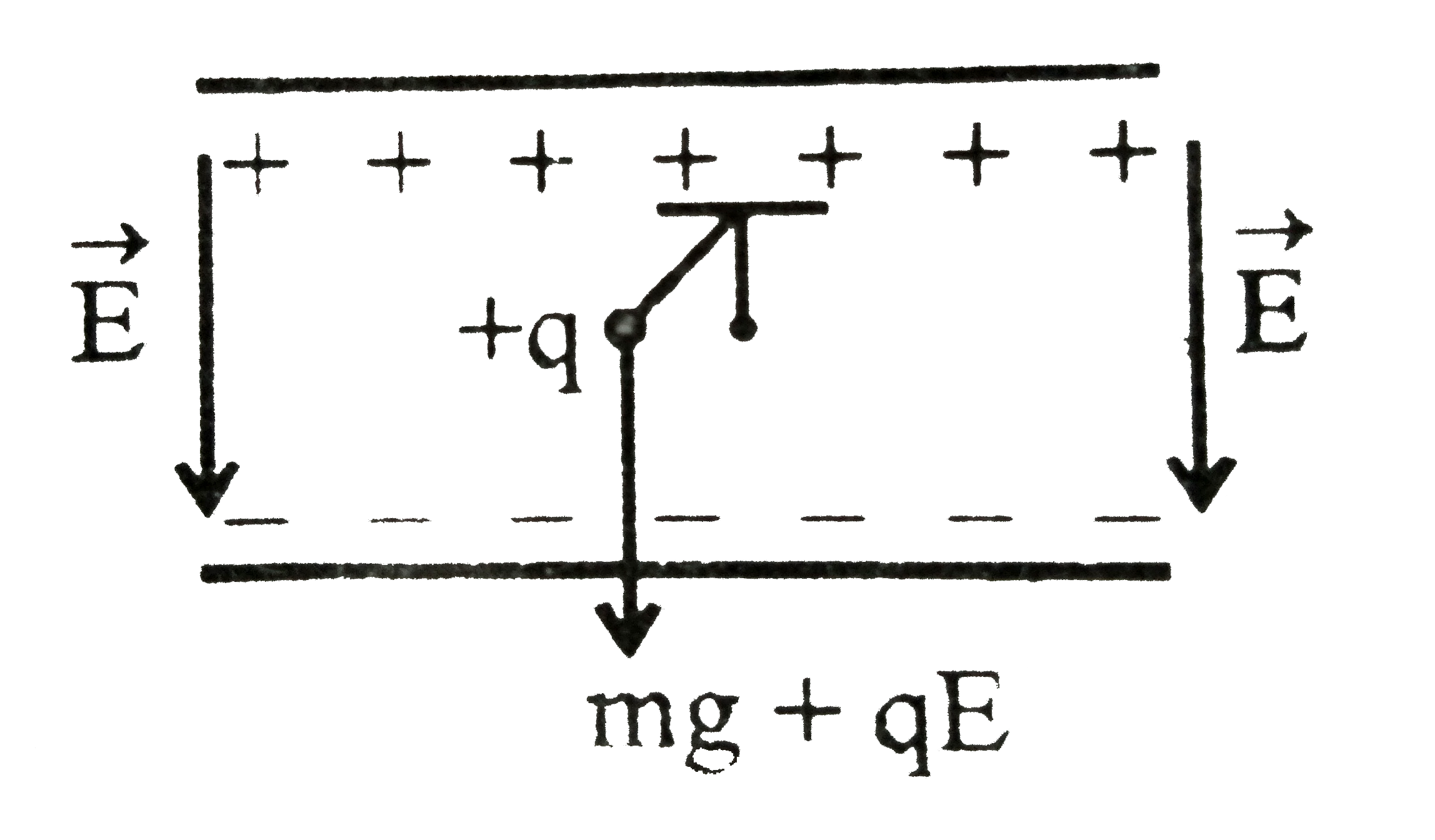
The time period of oscillation of the pendulum. if plates are held vertically , is given by :
View SolutionA particle of mass m carries an electric positive charge Q and is subjected to the combined action of gravity g and a uniform horizontal electric field of strength E,it is projected with speed u to the vertical plane parallel to the electrical field and at an angle θto the horizontal .The maximum distance the particle travels horizontally when it is at the same level as its starting point is
View Solution
Knowledge Check
A particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity
 AThe kinetic energy after a displacement y is qEyBThe horizontal and vertical components of acceleration of ax=0,ay=qEmCthe equation of trajectory is y=12(qEx2mv2)DThe horizontall and verticasl displacements x and y after a time t x=vt and y=12ayt2
AThe kinetic energy after a displacement y is qEyBThe horizontal and vertical components of acceleration of ax=0,ay=qEmCthe equation of trajectory is y=12(qEx2mv2)DThe horizontall and verticasl displacements x and y after a time t x=vt and y=12ayt2A particle of mass an charge q is projected vertically upwards .A uniform electric field →E is acted vertically downwards.The most appropiate graph between potential energy U (gravitaion plus eelectrostatic) and height h(lt lt radius of earth) is :(assume U to be zero on surface of earth)
A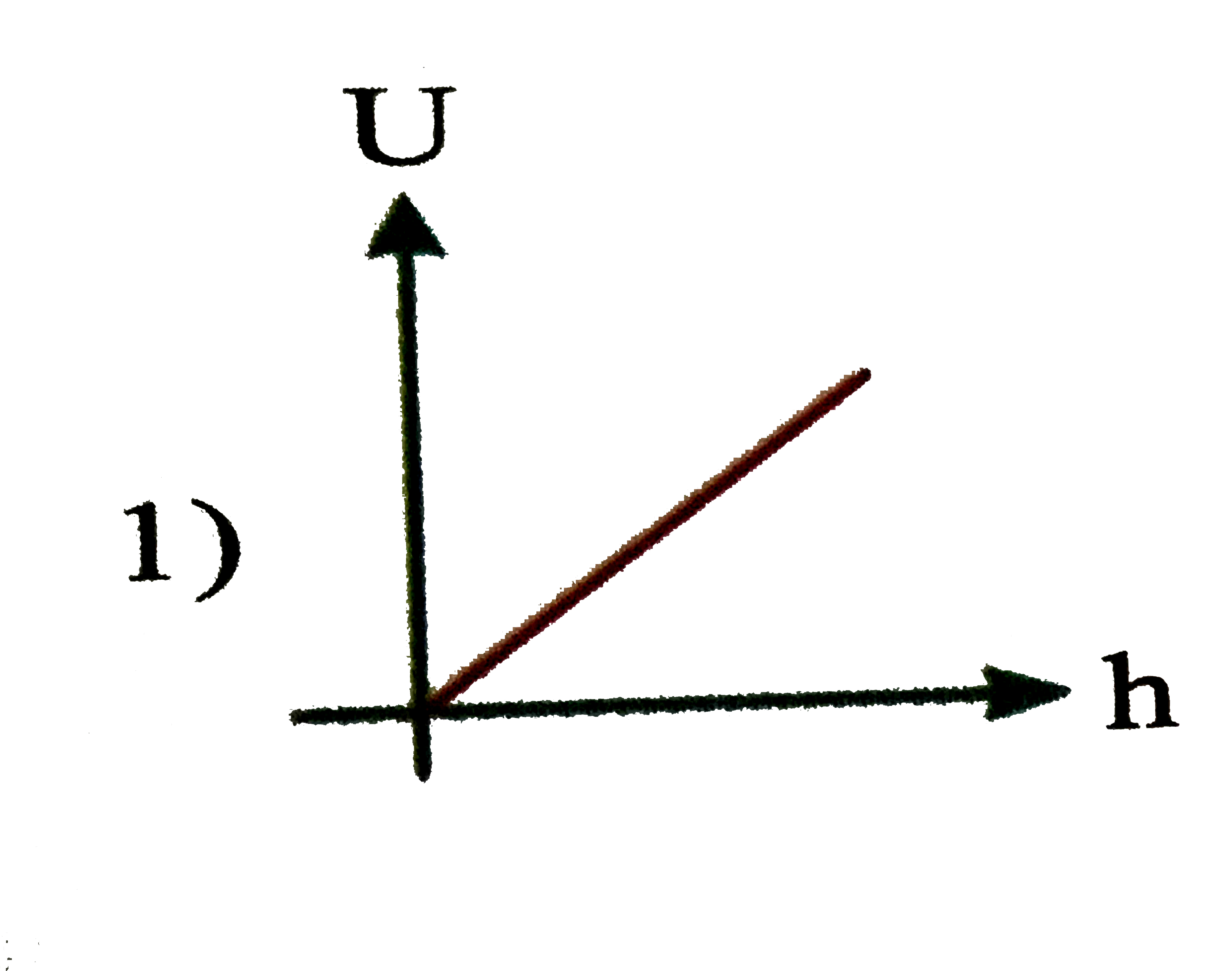 B
B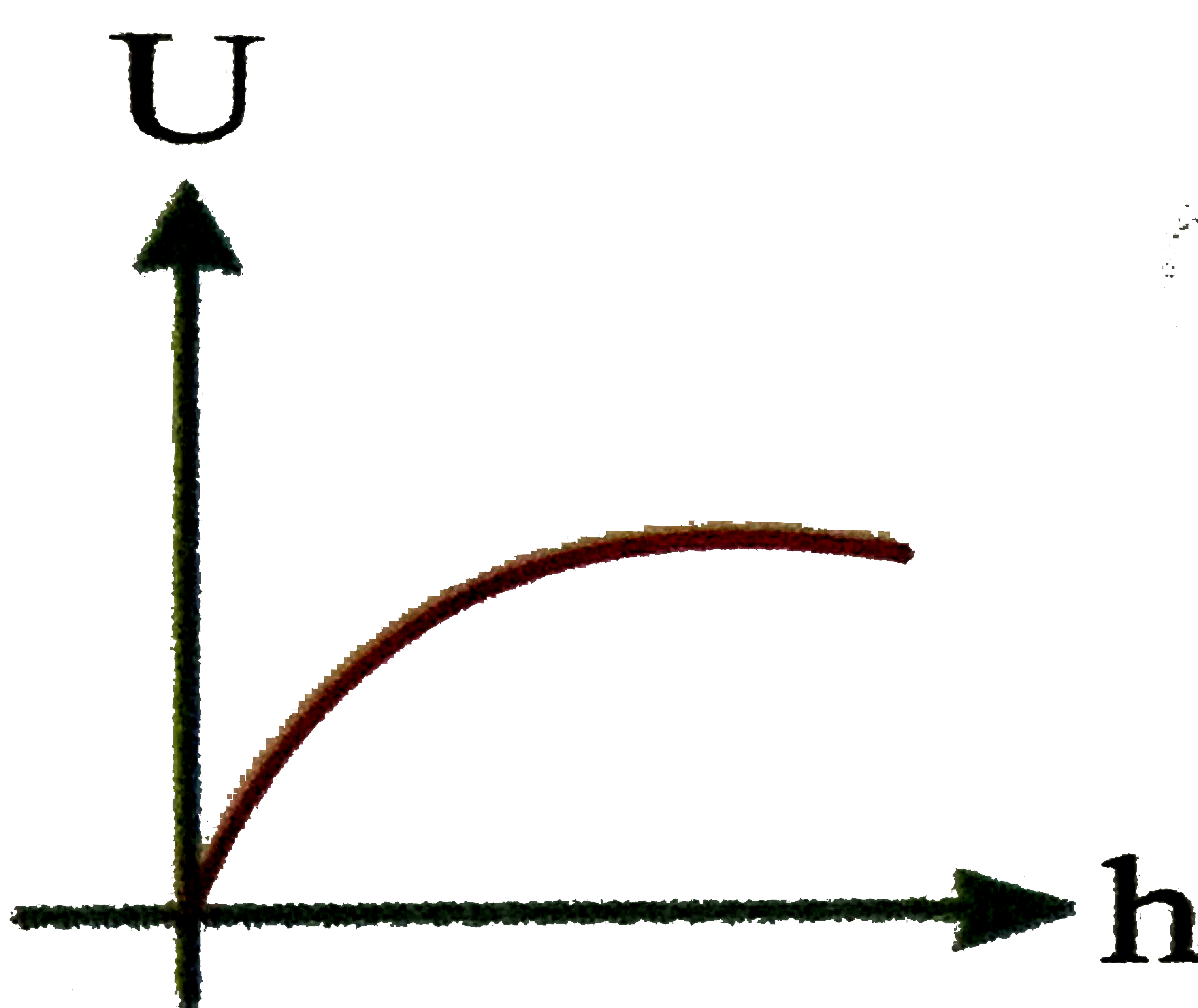 C
C D
D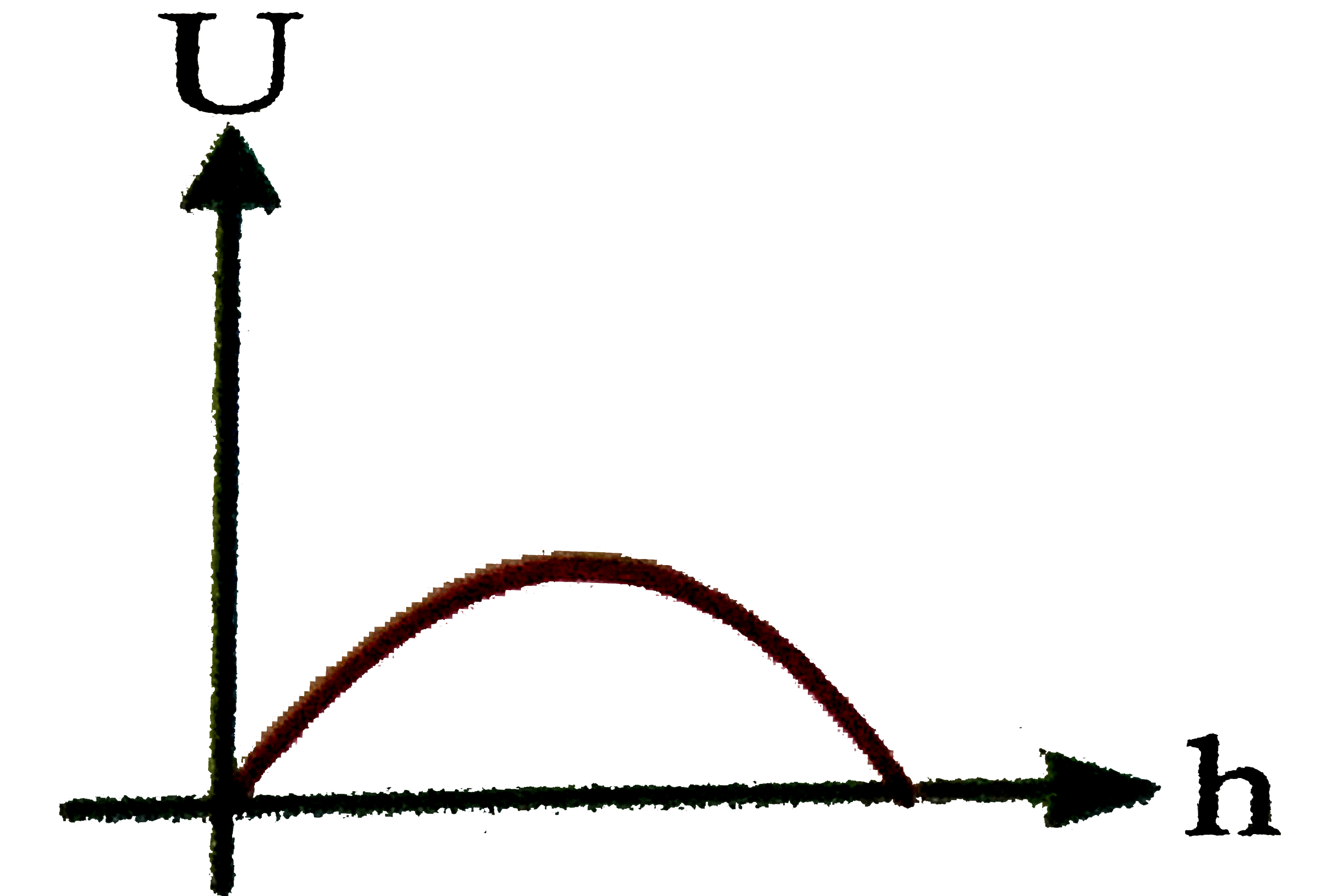
A simple pendulum having caharge q1 mass ma and effective length 1, is suspended from a rigid support between the plates of charged horizontal capacitor. Electric field in the capacitor is perpendicular to the plates and directed vertically downwards .
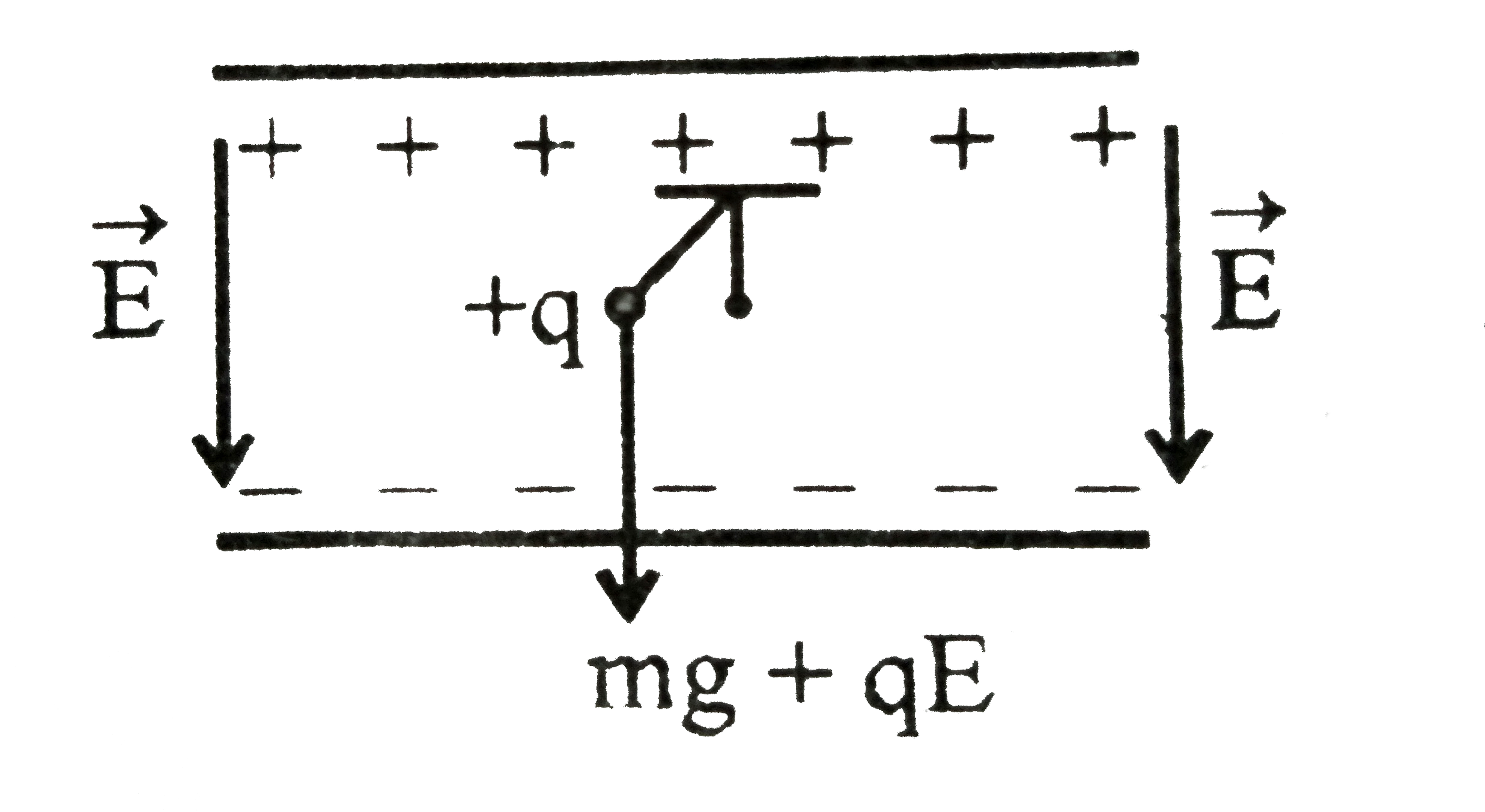
the angle α between the equilibrium position of the pendulum and the vertical is given by.Aα=sin−1[(qQE/m)sinθh+(qE/m)vodθ]Bα=cos−1[(qQE/m)sinθh+(qE/m)vodθ]Cα=tan−1[(qQE/m)sinθh+(qE/m)vodθ]Dα=cos−1[(qQE/m)sinθh+(qE/m)vodθ]
A particle having mass m and charge q is projected at an angle of 75° to the horizontal with a speed u. A uniform electric field E=mgq exists in horizontal direction. Find the time after projection when the velocity of particle makes an angle of 45° with horizontal.
View SolutionA simple pendulum having caharge q1 mass ma and effective length 1, is suspended from a rigid support between the plates of charged horizontal capacitor. Electric field in the capacitor is perpendicular to the plates and directed vertically downwards .
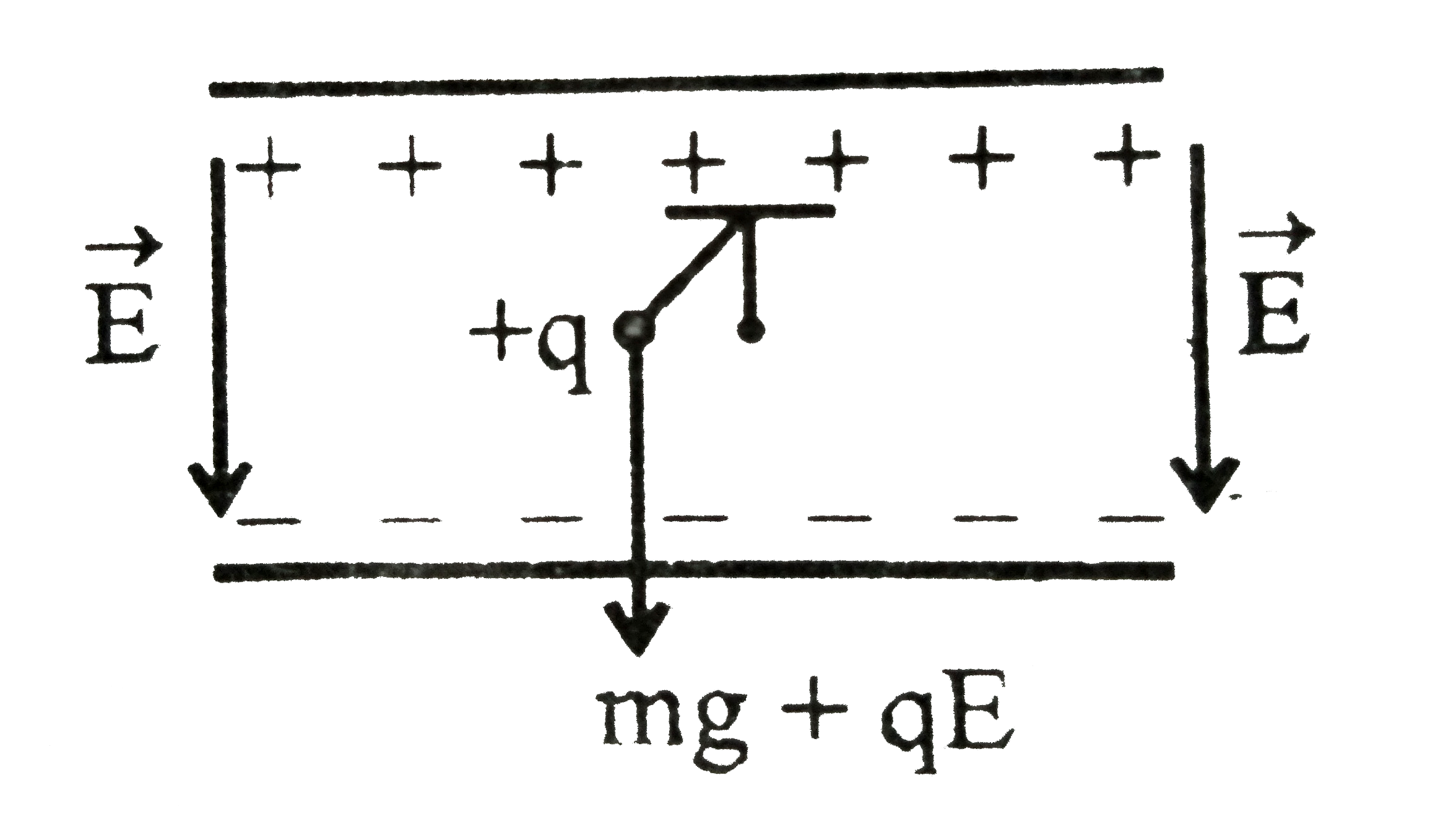
The time period of socillattion of the pendulum is given by :
View SolutionA charged particle of mass 5×10−5kg is held stationary in space by placing it in an electric field of strength 107NC−1 directed vertically downwards. The charge on the particle is
View SolutionA particle is moving towards east enters in a magnetic field directed towards north and deflected in vertically downward direction. The charged particle is
View SolutionTwo particles A and B having different masses arc projected from a tower with same speed. A is projected vertically upward and B vertically downward. On reaching the ground
View Solution
