A dielectric having dielectric constant k =4 is filled in a capacitor having length l and width b now length of capacitor is increased by l1 for which energy stored become half of initial value l1 should be
2l
6l
8l
4l
The correct Answer is:D
To solve the problem step by step, we need to analyze the situation involving a capacitor with a dielectric and how its energy changes when the length is increased.
Step 1: Understanding the Initial Configuration
The initial capacitor has a dielectric constant k=4, length L, and width b. The capacitance C1 of the capacitor filled with dielectric is given by the formula:
C1=k⋅ϵ0Ad
where A=L⋅b is the area of the plates, ϵ0 is the permittivity of free space, and d is the separation between the plates.
Step 2: Calculate Initial Capacitance
Substituting the area into the capacitance formula:
C1=4⋅ϵ0(L⋅b)d=4ϵ0Lbd
Step 3: Calculate Initial Energy Stored
The energy U1 stored in the capacitor is given by:
U1=12C1V2
where V is the voltage across the capacitor.
Step 4: New Configuration After Length Increase
When the length of the capacitor is increased by l1, the new length becomes L+l1. The new capacitance C2 of the capacitor (with the dielectric still in place) is:
C2=k⋅ϵ0A′d
where A′=(L+l1)⋅b. Thus,
C2=4⋅ϵ0((L+l1)⋅b)d=4ϵ0(L+l1)bd
Step 5: Calculate New Energy Stored
The new energy U2 stored in the capacitor is:
U2=12C2V2
According to the problem, this new energy is half of the initial energy:
U2=12U1
Step 6: Setting Up the Equation
Substituting the expressions for U1 and U2:
12C2V2=12(12C1V2)
This simplifies to:
C2=12C1
Step 7: Substitute Capacitance Values
Substituting the capacitance values we derived:
4ϵ0(L+l1)bd=12(4ϵ0Lbd)
Cancelling common terms:
4(L+l1)=2L
Step 8: Solve for l1
Rearranging the equation gives:
4L+4l1=2L
4l1=2L−4L
4l1=−2L
l1=−L2
Conclusion
The length l1 by which the capacitor's length should be increased to make the energy stored half of the initial value is:
l1=−L2
This indicates that the length cannot be increased positively to achieve the condition; instead, it suggests a conceptual misunderstanding in the problem setup.
The initial capacitor has a dielectric constant k=4, length L, and width b. The capacitance C1 of the capacitor filled with dielectric is given by the formula:
C1=k⋅ϵ0Ad
where A=L⋅b is the area of the plates, ϵ0 is the permittivity of free space, and d is the separation between the plates.
Substituting the area into the capacitance formula:
C1=4⋅ϵ0(L⋅b)d=4ϵ0Lbd
The energy U1 stored in the capacitor is given by:
U1=12C1V2
where V is the voltage across the capacitor.
When the length of the capacitor is increased by l1, the new length becomes L+l1. The new capacitance C2 of the capacitor (with the dielectric still in place) is:
C2=k⋅ϵ0A′d
where A′=(L+l1)⋅b. Thus,
C2=4⋅ϵ0((L+l1)⋅b)d=4ϵ0(L+l1)bd
The new energy U2 stored in the capacitor is:
U2=12C2V2
According to the problem, this new energy is half of the initial energy:
U2=12U1
Substituting the expressions for U1 and U2:
12C2V2=12(12C1V2)
This simplifies to:
C2=12C1
Substituting the capacitance values we derived:
4ϵ0(L+l1)bd=12(4ϵ0Lbd)
Cancelling common terms:
4(L+l1)=2L
Rearranging the equation gives:
4L+4l1=2L
4l1=2L−4L
4l1=−2L
l1=−L2
The length l1 by which the capacitor's length should be increased to make the energy stored half of the initial value is:
l1=−L2
This indicates that the length cannot be increased positively to achieve the condition; instead, it suggests a conceptual misunderstanding in the problem setup.
Topper's Solved these Questions
Similar Questions
A parallel plate capacitor has plate of length 'l' width 'w' and separation of plates is 'd' . It is connected to a battery of emf V . A dielectric slab of the same thickness 'd' and of dielectric constant k=4 is being inserted between the plates of the capacitor . At what lenght of the slab inside plates , will the energy stored in the capacitor be two time the initial energy stored ?
View SolutionTwo parallel plate capacitors of capacitances C1 and C2 such that C2=2C1 are connected across battery of V volts as shown in the Fig . Initially the key K is kept closed to fully charge the capacitors . The key K is now thrown open and dielectric slabs of dielectric constant K0 are inserted in the two capacitors to completely fill the gap between the plates .

Find the ratio of the energies stored in the combination before and after the introduction of dielectric slabs .
View Solution
Knowledge Check
A cylindrical capacitor has charge Q and length L. If both the charge and length of the capacitor are doubled by keeping other parameters fixed, the energy stored in the capacitor
Aremains same.Bincreases two times.Cdereases two times.Dincreases four times.A capacitor having capacitance 1μF with air, is filled with two dielectrics as shown. How many times capacitance will increase?
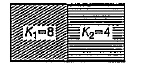 A12B6C8/3D3
A12B6C8/3D3A capacitor having capacitance 1μF with air is filled with two dielectrics as shown. How many times capacitance will increase ?
 A12B6C8/3D3
A12B6C8/3D3
A dielectric of dielectric constant 3 fill up three fourths of the space between the plates of a paralleled plate capacitor. The fraction of total energy that is stored in the dielectric is
View SolutionIf half the space between two concentric conducting spheres be filled with dielectric of dielectric constant k and the rest is filled with air. Show that the capacitance of the capacitor thus formed will be same as if the whole part is filled with the dielectric of dielectric constant 12(1+k):
View SolutionTwo dielectric slabs of constant K1 and K2 have been filled in between the plates of a capacitor as shown below. What will be the capacitance of the capacitor
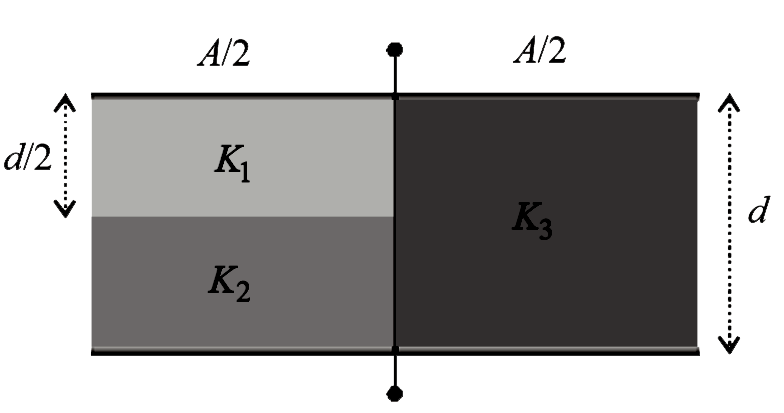
View SolutionA capacitor having capacitance 1μF with air is filled with two dielectrics as shown. How many times capacitance will increase ?

View SolutionA parallel plate capacitor with a dielectric slab with dielectric constant k=3 filling the space between the plates is charged to potential V and isolated. Then the dielectric slab is drawn out and another dielectric slab of equal thickness but dielectric constant k'=2 is introduced between the plates. The ratio of the energy stored in the capacitor later to that initially is:
View Solution
