The Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
1:1
1:2
2:1
4:2
The correct Answer is:C
Here Ys=2YB,YsYB=21
Let WS & WB the weights hanged to steel & brass wires
ls=lB=l,AB=As=A,Δls=ΔlB=Δl
Y=WlAΔlorΔl=WlAY
asΔls=ΔlB
∴WslAYs=WBlAYB
WsWB=YBYB=21
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:CBSE COMPLEMENTARY MATERIALChapter:PROPERTIES OF MATTERExercise:NUMERICALS
Explore 23 Videos
- NEWTON'S LAWS OF MOTIONBook:CBSE COMPLEMENTARY MATERIALChapter:NEWTON'S LAWS OF MOTIONExercise:Laws Of Motion
Explore 20 Videos
- ROTATIONAL MOTION Book:CBSE COMPLEMENTARY MATERIALChapter:ROTATIONAL MOTION Exercise:MULTIPLE CHOICE QUESTIONS
Explore 20 Videos
Similar Questions
The Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
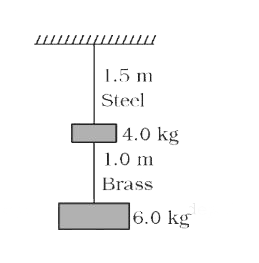
View Solution
Knowledge Check
The Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
A1:1B1:2C2:1D4:1Two wires A and B have the same length and area of cross-section. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
A1B2C12D√2The Young's modulii of brass ans steel are in the ratio of 1:2. A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If rB and rS are the radii of brass and steel wires respectively, then
ArS=rB2BrS=rB√2CrS=√2rBDrS=2rB
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in fig. The unloaded length of steel wire is 1.5m and that of brass wire is 1.0m. Compute the elongations of the steel and the brass wires.

View SolutionRigidity modulus of steel is η and its Young's modulus is Y. A piece of steel of cross sectional area A is chaged into a wire of length L and area A10 then :
View SolutionYoung's modulus of steel is Y and its rigidity modulus is η. A piece of steel of cross-sectional area A, is stretched into a wire of length L and area of cross-section A4, In wire case
View SolutionAn iron wire an copper wire having same length and cross-section are suspended form same roof Young's modulus of copper is 1/3rd that of iron. Then the ratio of the weighs to be added at their ends so that their ends are at the same level is
View SolutionA light rod of length 2 m is suspended ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is ade of steel and is of cross-section 0.1 cm and the other of brass of cross-section 0.2 cm. Along the rod at what distance a weight may be hung to produce stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)
View Solution
