Two coherent light sources A and B with separation 2λ or placed on the x-axis symmetrically about the origin. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and centre at the origin.
For P to have maximum intensity , dcosθ=nλ
2λcosθ=nλcosθ=n2 where n is integer
For n=0,θ=900,2700
n=±1,θ=600,1200,2400,3000
n=±2,θ=00,1800
So, positions of maxima are at
θ=00,600,900,1200,1800,2400,2700and3000,
i.e., 8 positions will be obtained,
Short cut : In d=nλ then number of maximum on the circle is 4n . Not : For minima ,
Δx=(2n−1)λ2

Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - Evaluate yourself - 112videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - Evaluate yourself - 23videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II(H.W)19videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)19videos
SEMICONDUCTOR ELECTRONICS
Similar Questions
An inteference is observed due to two coherent sources A and B separated by a distance 4λ along Y-axis, where λ is the wavelength of light. A detector 'D' is moved alog the positive X-axis. Find the totla number of maxima observe on the X-axis excluding the points x=0 and x=∞ ?
 View Solution
View SolutionAn inteference is observed due to two coherent sources A and B separated by a distance 4λ along Y-axis, where λ is the wavelength of light. A detector 'D' is moved alog the positive X-axis. Find the total number of maxima observe on the X-axis excluding the points x=0 and x=∞ ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
A20B22C24D26 - Question 2 - Select One
Two coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
 A3λB8λC5λ/4D8.75λ
A3λB8λC5λ/4D8.75λ - Question 3 - Select One
_E01_036_Q01.png)
Two point source separated by d=5μm emit light of wavelength λ=2μm in phase A cicular wire of radius 20μm is placed aournd the source as shown in figure.APoints A and B are dark and points C and D are bright.BPoint A and B are bright and point C and D are darkCPoint A and C are dark and points B and D are bright.DPoints A and C are bright and points B and D are dark.
A point charge q is placed at origin. Find the flux of electric,produced due to this charge, through a circle of radius R lying in y-z plane. The centre of the circle lies at (x,0).
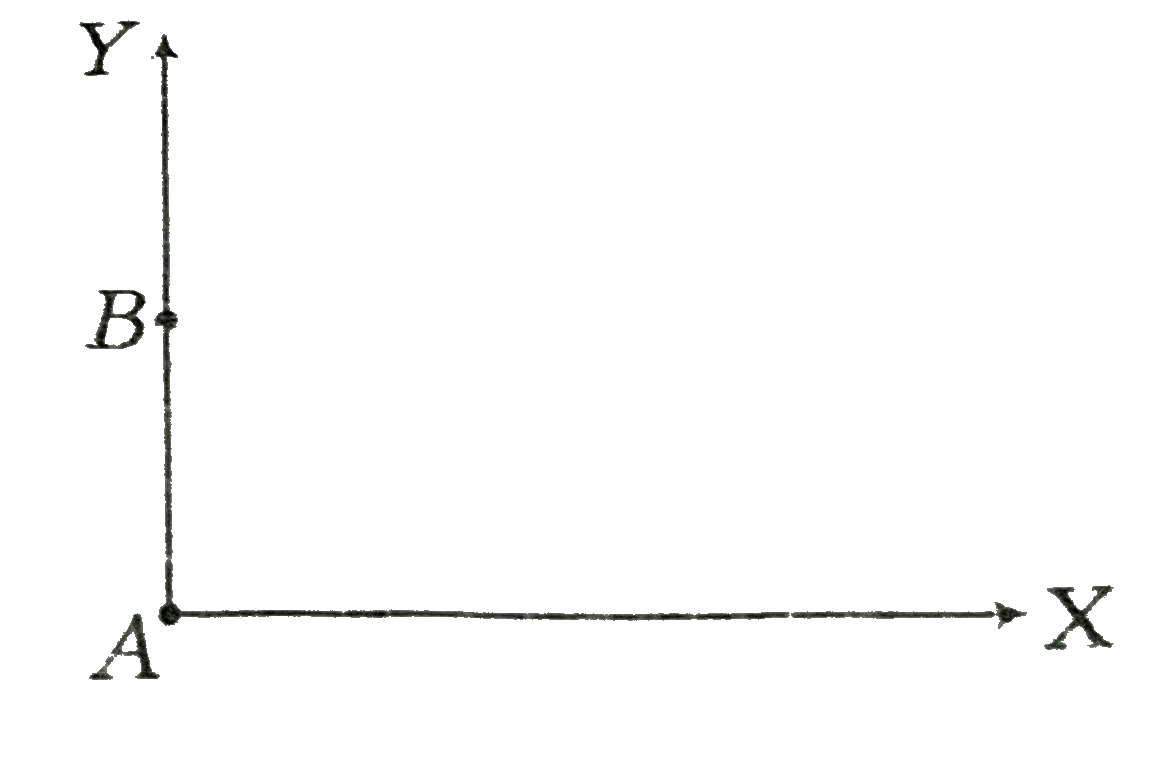
View SolutionTwo coherent sources A & B emitting light of wavelength lambda are placed at position (-D,0) and (−D,3λ) respectively Here D >>λ The number of minima on y-axis and maxima on x-axis respectively are
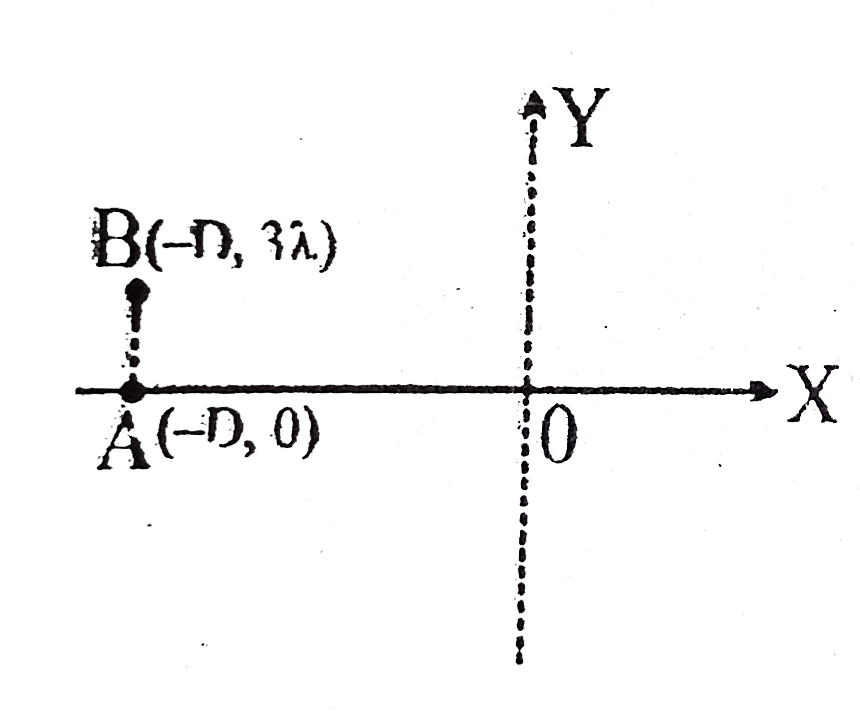 View Solution
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=nλ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
View SolutionTwo coherent sources emit light of wavelength λ. Separation between them, d=4λ.
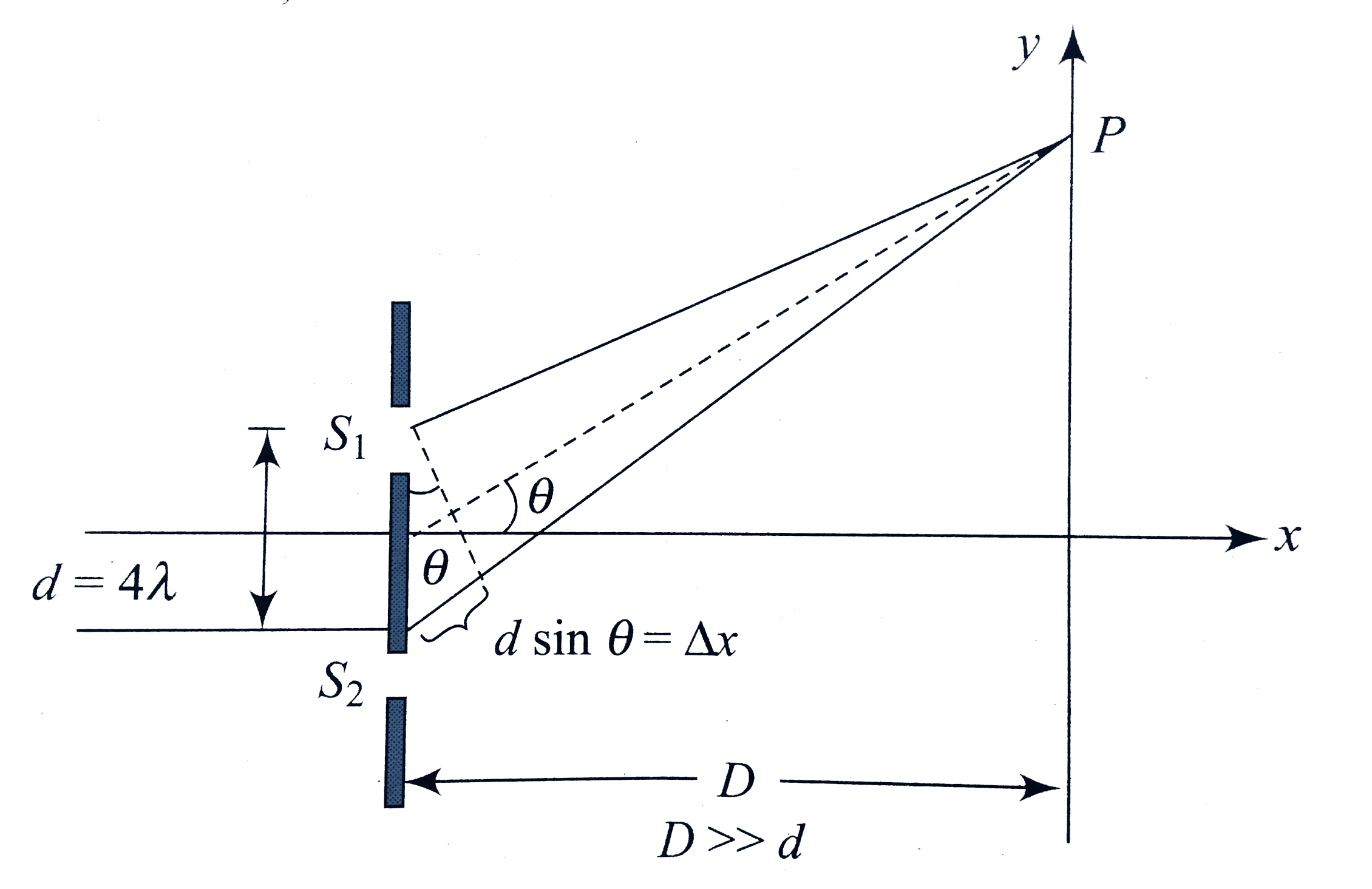
If a detector moves along the y-axis, what is the maximum number of minima observed?View Solution

