Consider the optical system whown in fig. the point source of light S is having wavelength equal to λ . The light is reaching screen only after refection . For point P to be 2 nd maxima, the value of λ would be (S>>d&d>>λ)
1. 12d2D , 2. 6d2D ,
3. 3d2D , 4. 24d2D

a. At P, Δx(8d)×3dD
For 2nd maxima , Δx=2λ,⇒24d2D=2λ
⇒λ=12d2D

Topper's Solved these Questions
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - Evaluate yourself - 1
12 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - Evaluate yourself - 2
3 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II(H.W)
19 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
19 Videos
Similar Questions
Consider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)
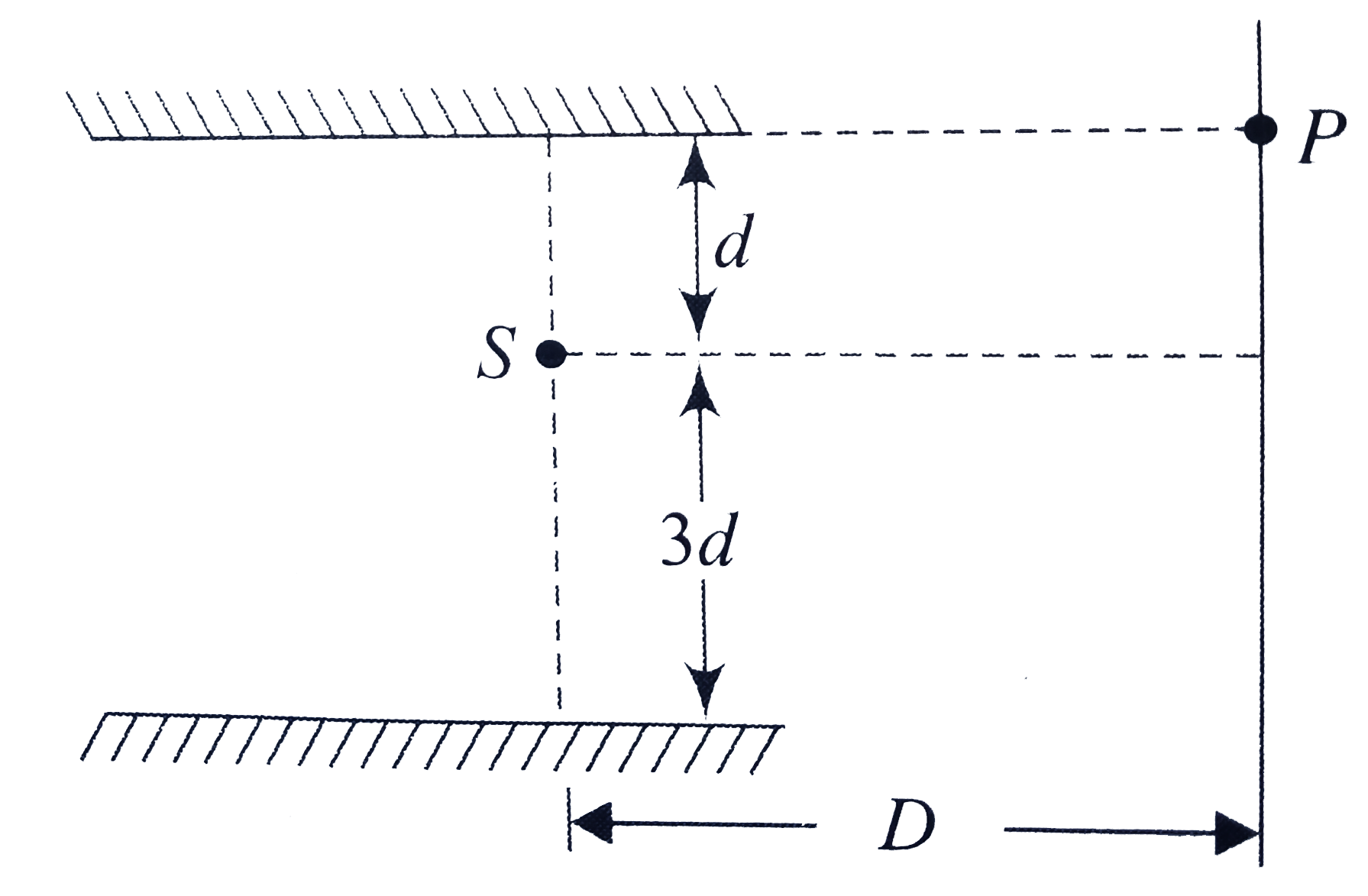
View SolutionConsider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)

View Solution
Knowledge Check
Consider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)
 A12d2DB6d2DC3d2DD24d2D
A12d2DB6d2DC3d2DD24d2DTwo points nonochromatic and coherent sources of light of wavelength λ each are placed as shown in figure. The initial phase difference between the sources is zero O. (d>>d). Mark the correct statement(s).
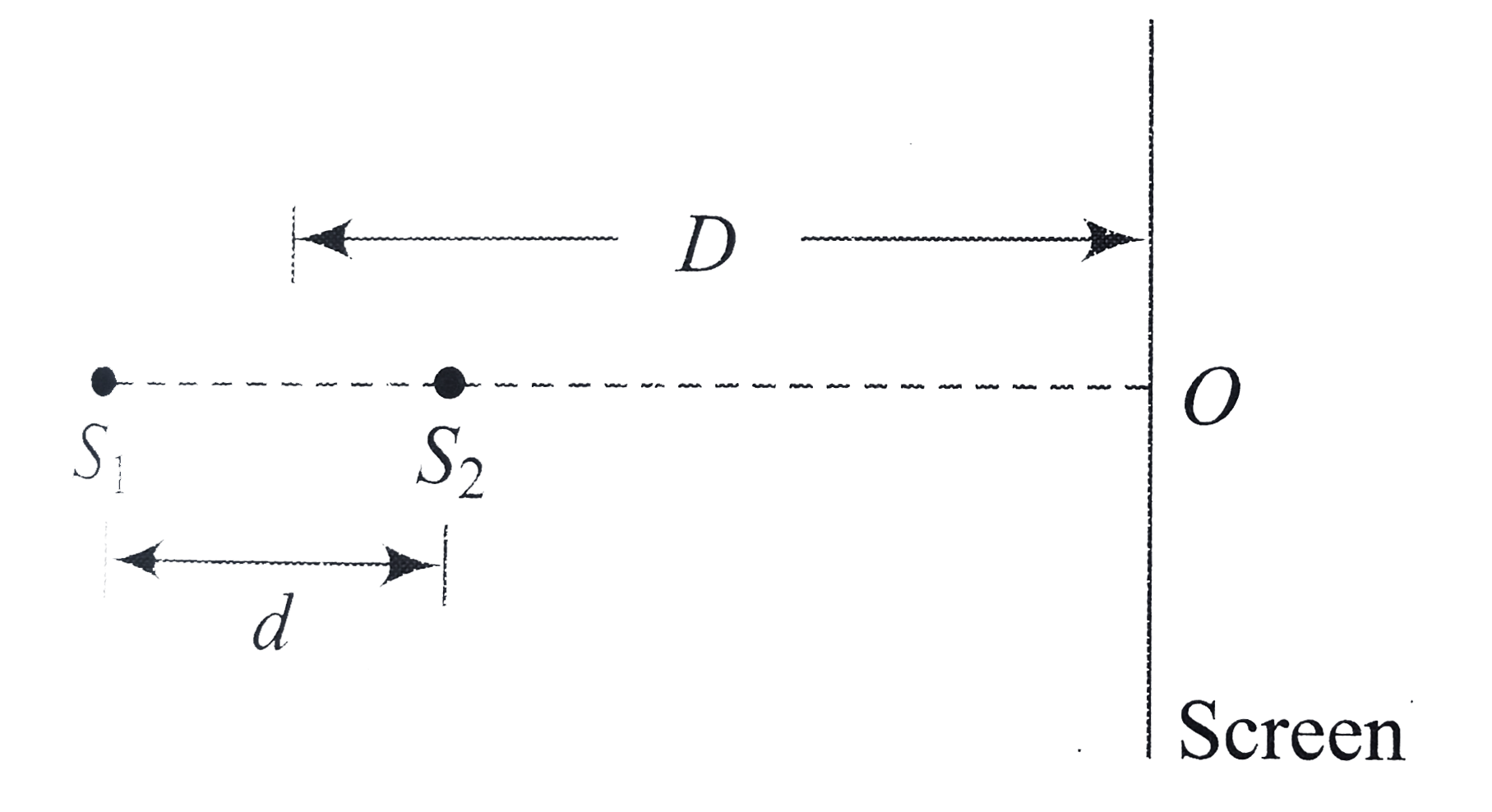 AIf d=7λ2, O will be a minimaBIf d=λ, only one maxima can be observed on the screenCIf d=4.8λ, then total 10 minima would be there on the screenDIf d=5λ2, the intensity at O would be minimum.
AIf d=7λ2, O will be a minimaBIf d=λ, only one maxima can be observed on the screenCIf d=4.8λ, then total 10 minima would be there on the screenDIf d=5λ2, the intensity at O would be minimum.Two points nonochromatic and coherent sources of light of wavelength λ each are placed as shown in figure. The initial phase difference between the sources is zero O. (d>>d). Mark the correct statement(s).
 AIf d=7λ2,O will be minima.BIf d=λ, only one maxima can be observed on screen.CIf d=4.8λ then total 10 minimas would be there on screen.DIf d=5λ2, then intensity at O would be maximum.
AIf d=7λ2,O will be minima.BIf d=λ, only one maxima can be observed on screen.CIf d=4.8λ then total 10 minimas would be there on screen.DIf d=5λ2, then intensity at O would be maximum.
Four monochromatic and coherent sources of light, emitting waves in phase of wavelength λ, are placed at the points x = 0, d 2d and 3d on the x-axis. Then
View SolutionLight of wavelength λ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is
View SolutionA parallel beam of light of wavelength λ passes through a slit of width d. The transmitted light is collected on a screen D aways (D>>d). Find the distance between the two second order minima.
View SolutionLight of wavelength λ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is ––
View SolutionA parallel beam of light of wavelength λ passes through a slit of width d. The transmitted light is collected on a screen D aways (D>>d). Find the distance between the two second order minima.
View Solution
