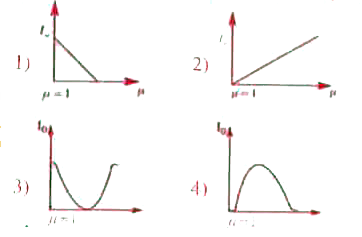
In a YDSE experiment if a slab whose refractive index can be baried is placed in front of one of the slits, then the variation of resultant intensity at mid - point of screen with 'μ' will be best respresented by (μ>1) .
[Assume slits of equal width and there is no absorption by slab]
![In a YDSE experiment if a slab whose refractive index can be baried is placed in front of one of the slits, then the variation of resultant intensity at mid - point of screen with 'mu' will be best respresented by (mu gt 1) . [Assume slits of equal width and there is no absorption by slab]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NAR_NEET_PHY_XII_P3_C10_SLV_024_Q01.png)
Δx=(μ−1)t,Forμ=1,Δx=0
∴I = maximum = I0,Asμ increases path difference Δx also increases . , For Δx=0toλ2 , intensity will decrease from I0 to zero .
The for Δx=λ2toλ , intensity will increase from zero to I0
Hence option 3 is correct
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - Evaluate yourself - 112videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - Evaluate yourself - 23videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II(H.W)19videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)19videos
SEMICONDUCTOR ELECTRONICS
Similar Questions
In YDSE if a slab whose refractive index can be varied is placed in front of one of the slits. Then, the variation of resultant intensity at mid-point of screen with μ will be best represented by (mu is greater than or equal to 1)
View SolutionIn YDSE if a slab whose refractive index can be varied is placed in front of one of the slits. Then, the variation of resultant intensity at mid-point of screen with μ will be best represented by (mu is greater than or equal to 1)
View Solution
Knowledge Check
- Question 1 - Select One
In YDSE if a slab whose refractive index can be varied is placed in front of one of the slits. Then, the variation of resultant intensity at mid-point of screen with μ will be best represented by (mu is greater than or equal to 1)
A
B
C
D
- Question 2 - Select One
In Young's experiment, if a slab of mica of refractive index μ and thickness of t is introduced in the path of light from one of the slits, then number of fringes formed on the screen will –
ADecreaseBIncreasesCRemain unchangedDMove to one side - Question 3 - Select One
In YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
Aλ(2μ−1)B2λ(2μ−1)Cλ(μ−1)D2λ(2μ+1)
In a YDSE if a slab whose refractive index can be varied is palced in fron of one of the slits then the variation of resultant intensity of mid-point of screen with μ will be represented by (assume slits of equal width and there is no absorption by slab)
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionMinimum thickness of a mica sheet having μ=32 which should be placed in front of one of the slits in YDSE is required to reduce the intensity at the centre of screen to half of maximum intensity is
View SolutionMinimum thickness of a mica sheet having μ=32 which should be placed in front of one of the slits in YDSE is required to reduce the intensity at the centre of screen to half of maximum intensity is
View SolutionIn YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
View Solution