If R is the radius and A is the mass number, then log R versus log A graph will be
a straight linje
a parabola
an ellipse
none of these
The correct Answer is:A
To solve the problem of finding the relationship between log R and log A, we can follow these steps:
1. Understand the relationship between R and A:
The radius R of a nucleus is given by the formula:
R=R0A1/3
where R0 is a constant (approximately 1.2 Fermi or 1.2×10−15 meters) and A is the mass number.
2. Take the logarithm of both sides:
To find the relationship between logR and logA, we take the logarithm of the equation:
logR=log(R0A1/3)
3. Apply the properties of logarithms:
Using the property of logarithms that states log(ab)=loga+logb and log(ab)=bloga, we can rewrite the equation:
logR=logR0+logA1/3=logR0+13logA
4. Rearranging the equation:
We can rearrange this equation to express logR in terms of logA:
logR=logR0+13logA
5. Identify the linear relationship:
This equation can be rearranged to fit the form of a straight line y=mx+c:
logR=13logA+logR0
Here, y=logR, x=logA, the slope m=13, and the y-intercept c=logR0.
6. Conclusion about the graph:
The graph of logR versus logA will be a straight line with a slope of 13 and a y-intercept of logR0.
Final Answer:
The graph of logR versus logA will be a straight line with a slope of 13.
---
The radius R of a nucleus is given by the formula:
R=R0A1/3
where R0 is a constant (approximately 1.2 Fermi or 1.2×10−15 meters) and A is the mass number.
To find the relationship between logR and logA, we take the logarithm of the equation:
logR=log(R0A1/3)
Using the property of logarithms that states log(ab)=loga+logb and log(ab)=bloga, we can rewrite the equation:
logR=logR0+logA1/3=logR0+13logA
We can rearrange this equation to express logR in terms of logA:
logR=logR0+13logA
This equation can be rearranged to fit the form of a straight line y=mx+c:
logR=13logA+logR0
Here, y=logR, x=logA, the slope m=13, and the y-intercept c=logR0.
The graph of logR versus logA will be a straight line with a slope of 13 and a y-intercept of logR0.
The graph of logR versus logA will be a straight line with a slope of 13.
Topper's Solved these Questions
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:EVALUATE YOURSELF-2
Explore 9 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:EVALUATE YOURSELF-3
Explore 7 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:EXERCISE- 4 One or more than one correct answer type
Explore 13 Videos
Similar Questions
The graph between logk versus 1/T is a straight line.
View SolutionAtomic nucleus is central core of every atom in which the whole of positive charge and almost entire mass of atom is concentrated. It is a tiny sphere of a radius R is given by R=RoA1/3, where Ro=1.4×10−15m, a constant and A the mass number of nucleus
A graph between 'log(RR0), and 'logA'
View Solution
Knowledge Check
In the above question, the curve between log I and log R will be :
A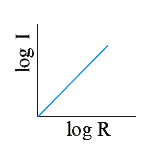 B
B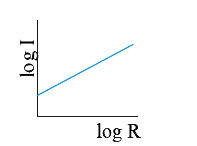 C
C D
D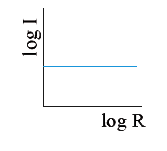
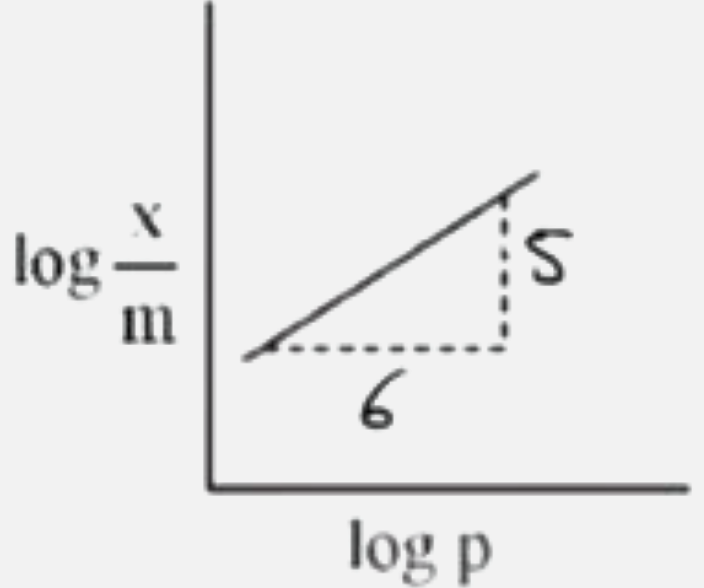
Adsorption of a gas follows Freundlich adsorption isotherm. x is the mass of the gas adsorbed on mass m of the adsorbent. The plot of logxm versus log p is shown in the graph. xm is proportional to:
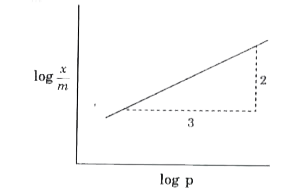 Ap2/3Bp3/2Cp3Dp2
Ap2/3Bp3/2Cp3Dp2For the adsorption of a gas on a solid, the plot of log(x/m) versus log p is linear with slope equal to
AkBlogkCnD1/n
If logx=2log(x+k) where x∈R+ and kis a positive real number then true act of values of k is
View SolutionThe intercept on Y - axis in the graph of log xm versus log P gives
View SolutionAdsorptions of gas follows Freundich adsorption isotherm . X is the mass of the gas adsorbed on mass m of the adsorbent. The plot of logxm versus log p is logxm shown in the given graph xm is propotional to:
View SolutionFor the adsorption of a gas on a solid, the plot of log(x/m) versus log P is linear with slope equal to:
View SolutionIn an adsorption experiment a graph between log xm versus log P was fond to be linear with a slope of 45∘). The intercept on the log xm axis was found to 0.70. Calculate the amount of gas adsorbed per gram of charcoal under a pressure of 1 atm [log5=0.70]
View Solution
