For a particle executing SHM along a straight line (displacement is measured from mean position).
Column - IColumn - II(a) velocity-time graph will be(p) straight line(b) acceleration-velocity graph may be(q) circle(c) acceleration-displacement graph will be(r) ellipse(d) acceleration-time graph will be(s) sinusoidal curve
a - s, b - q, r, c - p, d - s
a - p, b - s, r, c - s, d - p
a - q, b - s, r, c - p, d - s
a - r, b - q, r, c - q, d - s
The correct Answer is:A
To solve the problem of matching the items in Column I with those in Column II based on the characteristics of Simple Harmonic Motion (SHM), we will analyze each part step by step.
Step 1: Analyze the velocity-time graph
- Displacement in SHM: The displacement x(t) can be expressed as:
x(t)=Asin(ωt+ϕ)
- Velocity: The velocity v(t) is the derivative of displacement with respect to time:
v(t)=dxdt=Aωcos(ωt+ϕ)
- Graph Shape: Since v(t) is a cosine function, the velocity-time graph will be a sinusoidal curve.
Match: (a) velocity-time graph will be (s) sinusoidal curve.
Step 2: Analyze the acceleration-velocity graph
- Acceleration: The acceleration a(t) is the derivative of velocity:
a(t)=dvdt=−Aω2sin(ωt+ϕ)
- Relationship: We can express a in terms of v:
a=−ω2Av
Squaring both sides gives:
a2ω4A2+v2A2=1
- Graph Shape: This is the equation of an ellipse.
Match: (b) acceleration-velocity graph may be (r) ellipse.
Step 3: Analyze the acceleration-displacement graph
- Using SHM relationship: From a=−ω2x, we can express acceleration in terms of displacement:
a=−ω2x
- Graph Shape: This is a linear relationship, which represents a straight line.
Match: (c) acceleration-displacement graph will be (p) straight line.
Step 4: Analyze the acceleration-time graph
- Acceleration as a function of time: Since a(t)=−Aω2sin(ωt+ϕ), it is also a sinusoidal function.
- Graph Shape: Therefore, the acceleration-time graph will be a sinusoidal curve.
Match: (d) acceleration-time graph will be (s) sinusoidal curve.
Final Matches
- (a) → (s)
- (b) → (r)
- (c) → (p)
- (d) → (s)
Summary of Matches
- A → S
- B → R
- C → P
- D → S
- Displacement in SHM: The displacement x(t) can be expressed as:
x(t)=Asin(ωt+ϕ)
- Velocity: The velocity v(t) is the derivative of displacement with respect to time:
v(t)=dxdt=Aωcos(ωt+ϕ)
- Graph Shape: Since v(t) is a cosine function, the velocity-time graph will be a sinusoidal curve.
- Acceleration: The acceleration a(t) is the derivative of velocity:
a(t)=dvdt=−Aω2sin(ωt+ϕ)
- Relationship: We can express a in terms of v:
a=−ω2Av
Squaring both sides gives:
a2ω4A2+v2A2=1
- Graph Shape: This is the equation of an ellipse.
- Using SHM relationship: From a=−ω2x, we can express acceleration in terms of displacement:
a=−ω2x
- Graph Shape: This is a linear relationship, which represents a straight line.
- Acceleration as a function of time: Since a(t)=−Aω2sin(ωt+ϕ), it is also a sinusoidal function.
- Graph Shape: Therefore, the acceleration-time graph will be a sinusoidal curve.
- (a) → (s)
- (b) → (r)
- (c) → (p)
- (d) → (s)
- A → S
- B → R
- C → P
- D → S
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (H.W)
19 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - III
29 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - I (H.W)
66 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
2.The velocity-time (v-t) graph for a particle in straight line motion is given below the corresponding acceleration time graph will be?
View SolutionThe velocity - displacement graph of a particle moving along a straight line is shown
The most suitable acceleration - displacement graph will be

View Solution
Knowledge Check
The velocity-time graph of a particle is not a straight line. Its acceleration is
AzeroBconstantCnegativeDvariableIn SHM, acceleration versus displacement (from mean position) graph:
Ais always a straight line passing through origin and slope-1Bis always a stright line passing through origin and slope+1Cis always a stright line not necessarily passing through oringinDnone of the aboveThe velocity-displacement graph of a particle moving along a straight line is shown. The most suitable acceleration-displacement graph will be
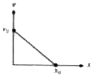 A
A B
B C
C D
D
A particle executes SHM. Then the graph of velocity as a function of displacement is
View SolutionA particle is executing SHM. Then the graph of acceleration as a function of displacement is
View Solution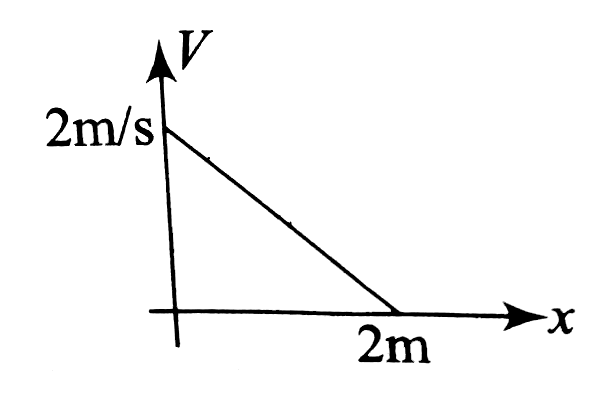
The velocity displacement graph of a particle moving along a straight line is shown in figure.
Then the acceleration displacement graph is.
View SolutionA particle is executing S.H.M. Then the graph of acceleration as a function of displacement is :
View SolutionA particle starts to move along a straight line. The acceleration versus time graph of particle is as shown in figure. The correct velocity versus time graph is :

View Solution
