The variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
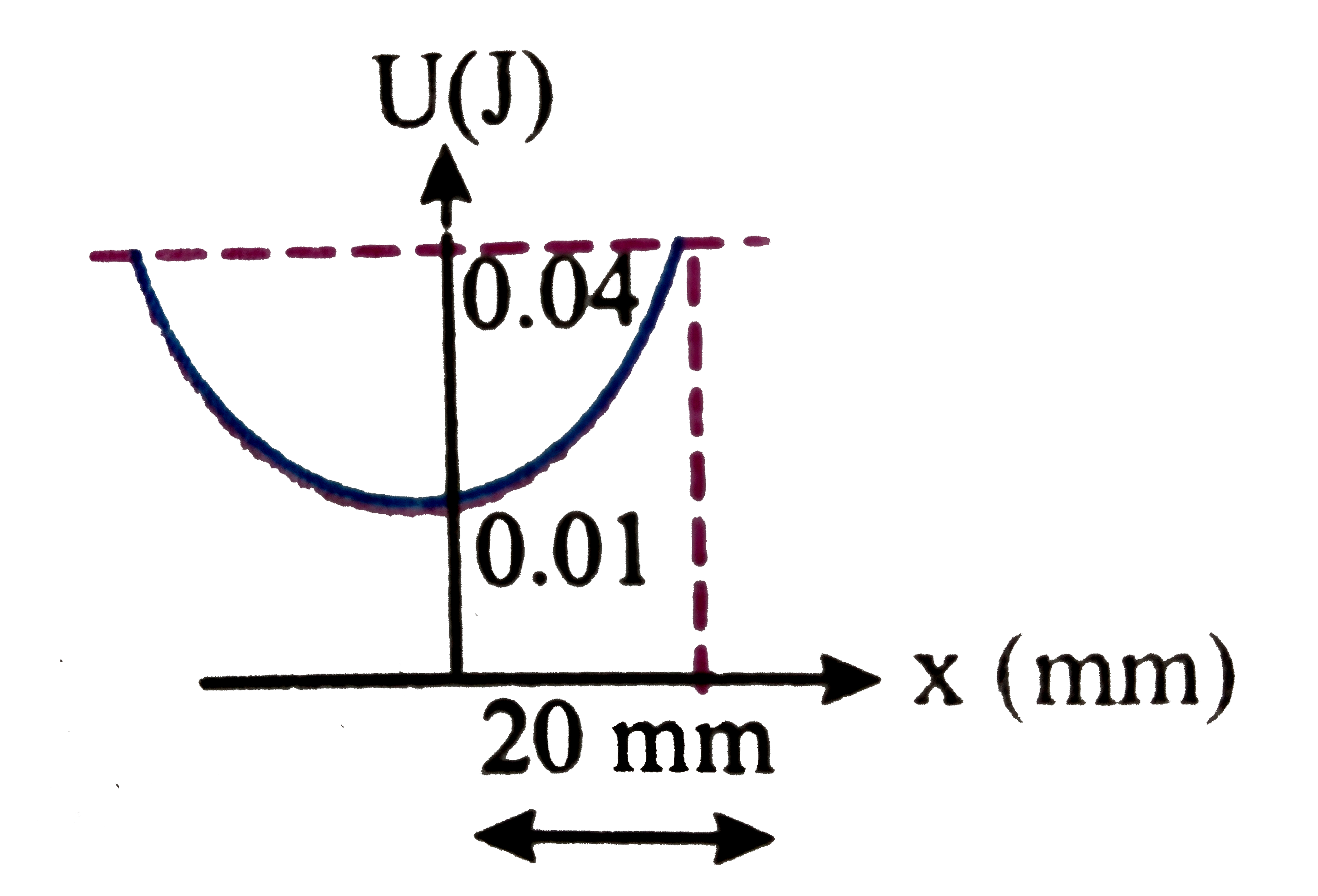
100 N/m
150 N/m
2003 N/m
300 N/m
The correct Answer is:B
Pe varies from zero to maximum. It is always positive sinusoidal function
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - III29videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV41videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (C.W)27videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
The veriation of potential energy of harmonic escillator is as shown in figure. The spring constant is
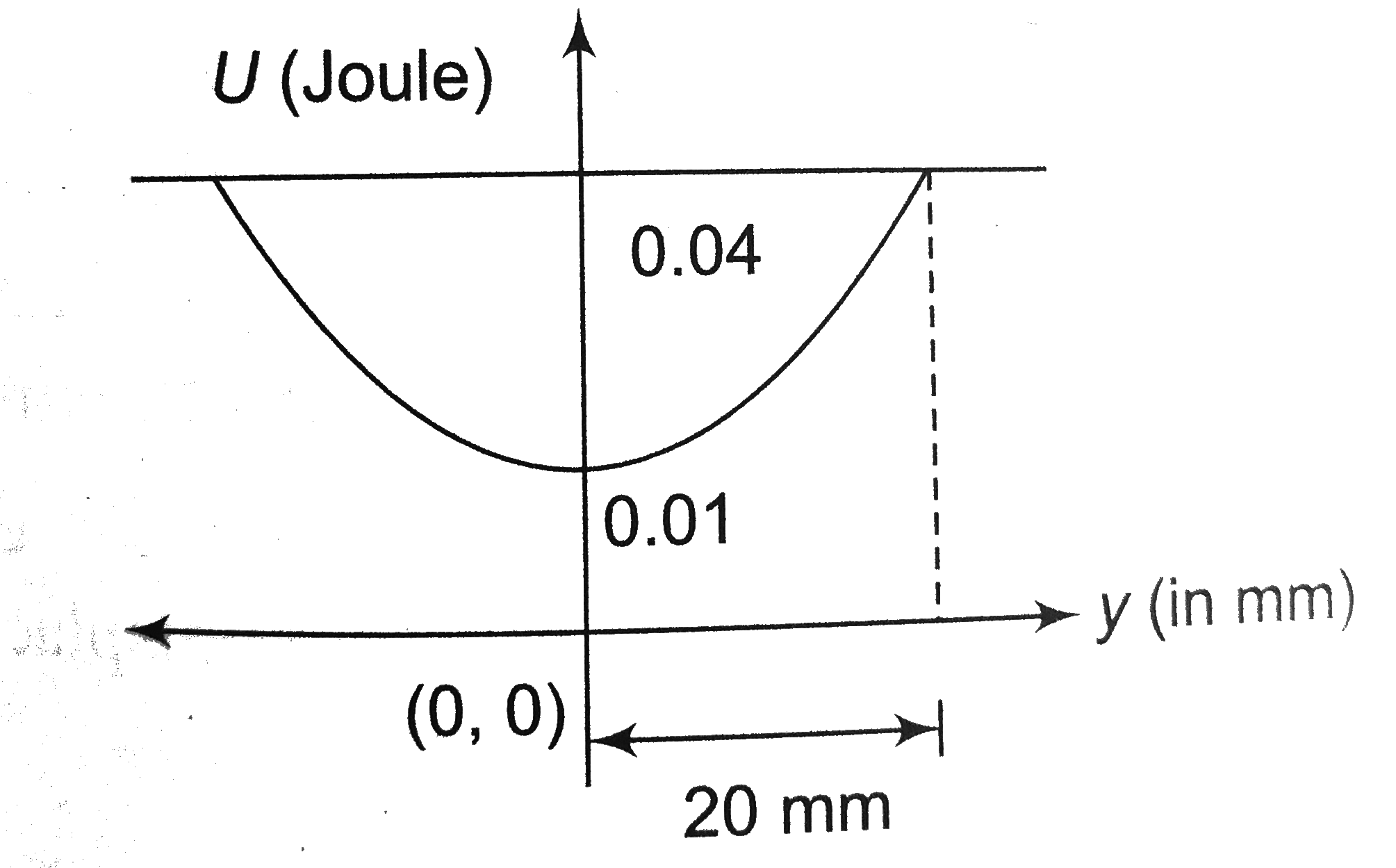 A1×102N/mB150N/mC0.667×102N/mD3×102N/m
A1×102N/mB150N/mC0.667×102N/mD3×102N/m - Question 2 - Select One
The variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
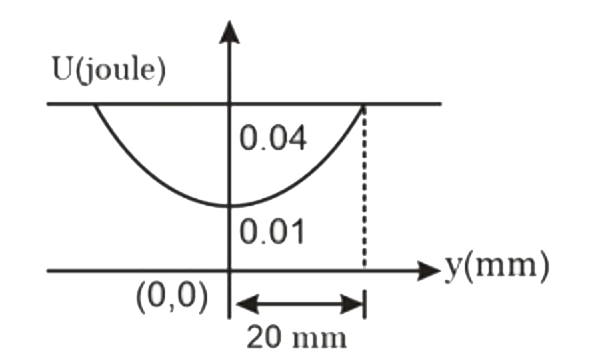 A1×102Nm−1B150Nm−1C66.7Nm−1D3×102Nm−1
A1×102Nm−1B150Nm−1C66.7Nm−1D3×102Nm−1 - Question 3 - Select One
The variation of potential energy U of a system is shown in figure. The force acting on the system is best represented by
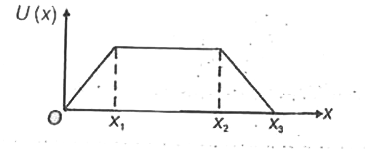 A
A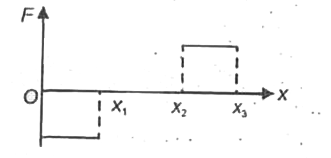 B
B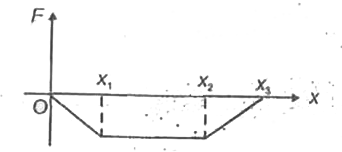 C
C D
D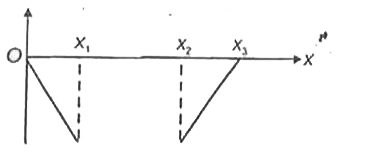
The maximum potential energy of a simple harmonic oscilator is Umax. The the P.E. of the oscillator when it is half way to its end point is
View SolutionFrequency of variation of kinetic energy of a simple harmonic motion of frequency n is
View SolutionThe variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for
 View Solution
View SolutionThe energy of a simple harmonic oscillator in the state of rest is 3 Joules. If its mean K.E. is 4 joules, its total energy will be :
View SolutionIf the total energy of a simple harmonic oscillator is E, then its potential energy, when it is halfway to its endpoint will be
View Solution

