If the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
23ms−2
−23ms−2
203ms−2
−203ms−2
The correct Answer is:D
Step by step video, text & image solution for If the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20 m//s to a value approaching zero at s = 30 m, determine the acceleration of the particle when s = 15 m. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The velocity of a particle moving in a straight line is decreasing at the rate of 3m/s per metre of displacement at an instant when the velocity is 10m/s. Determine the acceleration of the particle at this instant.
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View Solution
Knowledge Check
If the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
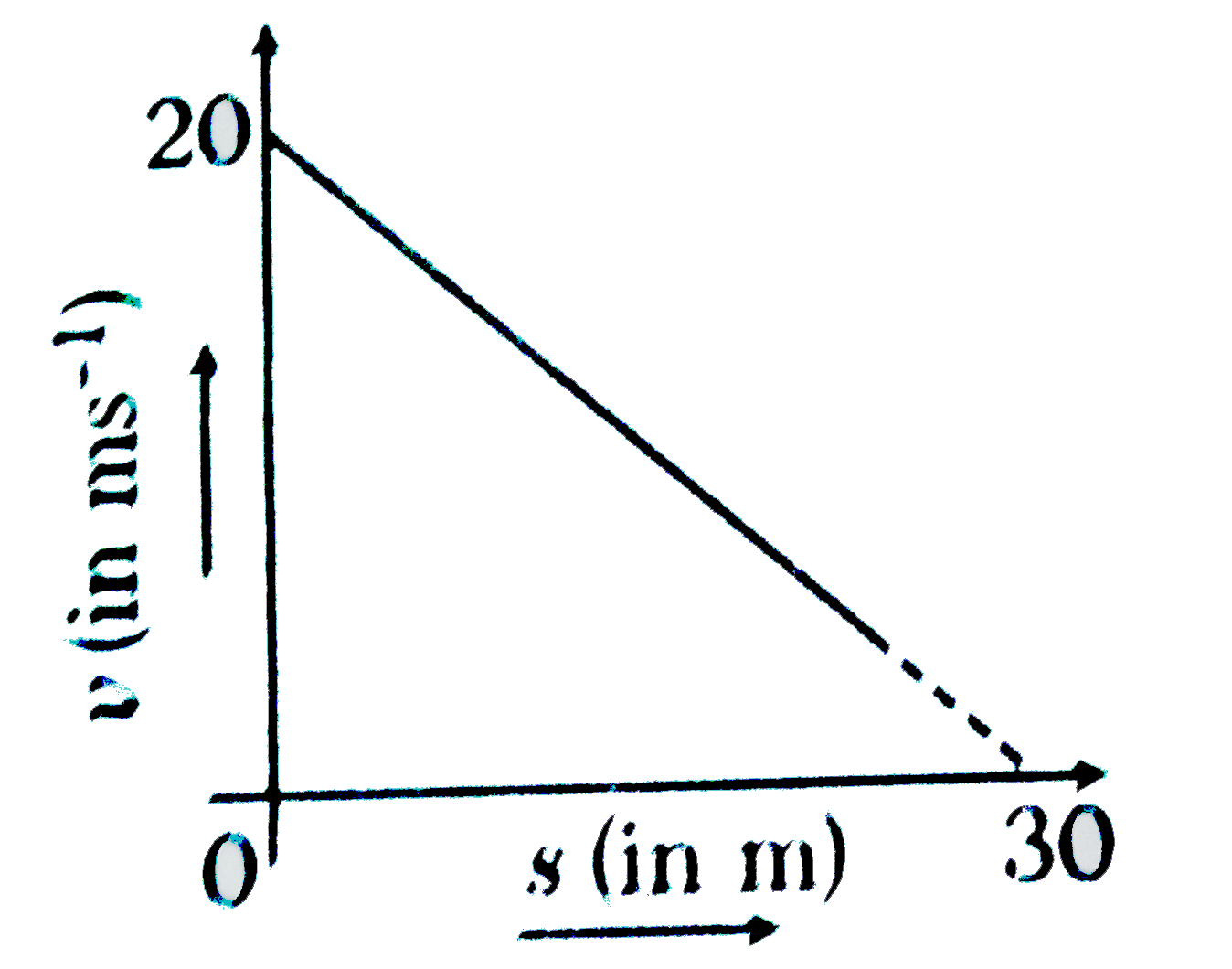 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2If the velocity v of a particle moving along a straight line decreases linearly with its position coordinates s from 50m/s to a value approaching zero at = 100 m, the time it takes to reach the 100 m position will be:
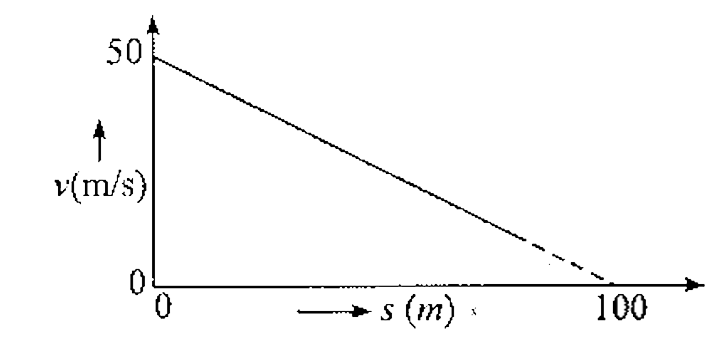 A10 sB5 sCInfinityD0.5 s
A10 sB5 sCInfinityD0.5 sIf the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by v2=a2+s2, then its acceleration equals
AasBsCs2D2s
A particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View SolutionA particle moves along a straight line such that its displacement s at any time t is given by s=t3−6t2+3t+4m, t being is seconds. Find the velocity of the particle when the acceleration is zero.
View SolutionIn a linear S.H.M., the acceleration of the particle is zero, when its velocity is
View SolutionFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :

View Solution
