A horizontal rod AB of length 1 is rotated with constant angular velocity ω about a vertical axis passing through end A. A non-uniform charge of the linear charge density λ=λ0x is distributed on the rod where x is the distance from the end A and λ0 is a constant.Find the ratio of the energy desity of magnetic field and electric field on the vertical line passing through A, at a point whose distance is 1 from the end A.
The correct Answer is:B, C
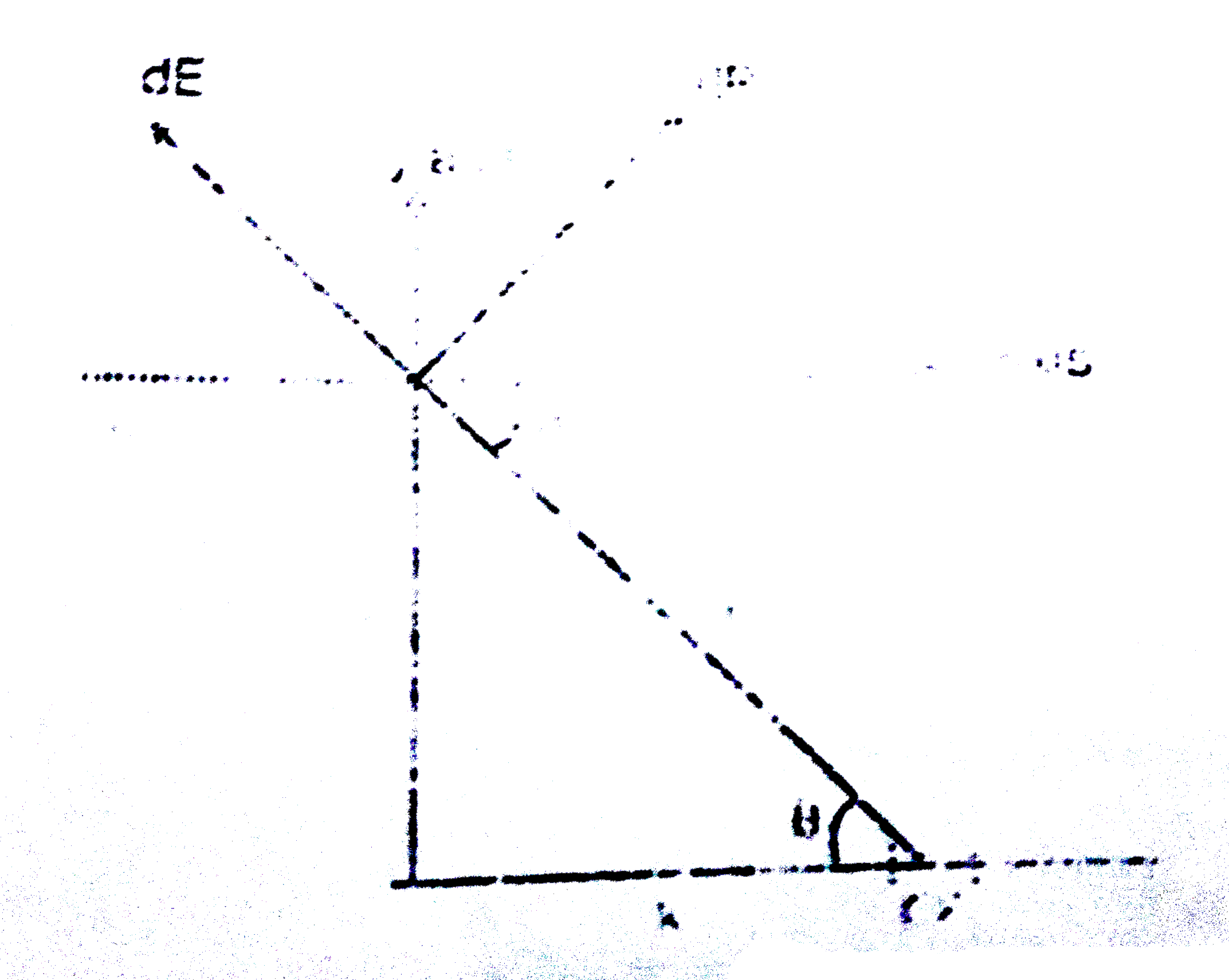
B=Bxˆi+Byˆj
where Bx=∫dBsinθ
By=∫dBcosθ
where dB=μ04π.(λ0X)(Xω)dxr2
similarly dE=K(λ0X)r2dx
E=Exˆi+Eyˆj
where Ex=∫dBcosθ
Ey=∫dBsinθ
Energy density ratio =B2/2μ012ε0E2=B2E2.c2 put the vaue of B &E and solve.
[Do not solve completely, it is vey lengthy]
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View Solution
Knowledge Check
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotationA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A mental rod AB of length l is rotated with a constant angular velocity ω about an axis passing through O and normal to its length . Potenial difference between ends of rod in absence of external magnetic field ( Where , e = electric change)
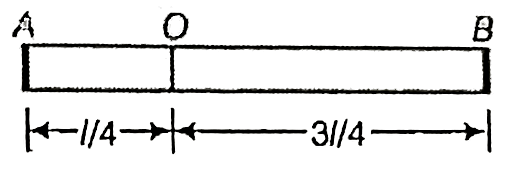 AzeroBmω2l24eCmω2l22eDmω2l28e
AzeroBmω2l24eCmω2l22eDmω2l28e
Find coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View Solutionthe linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
View SolutionA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
View Solutionthe linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View Solution
