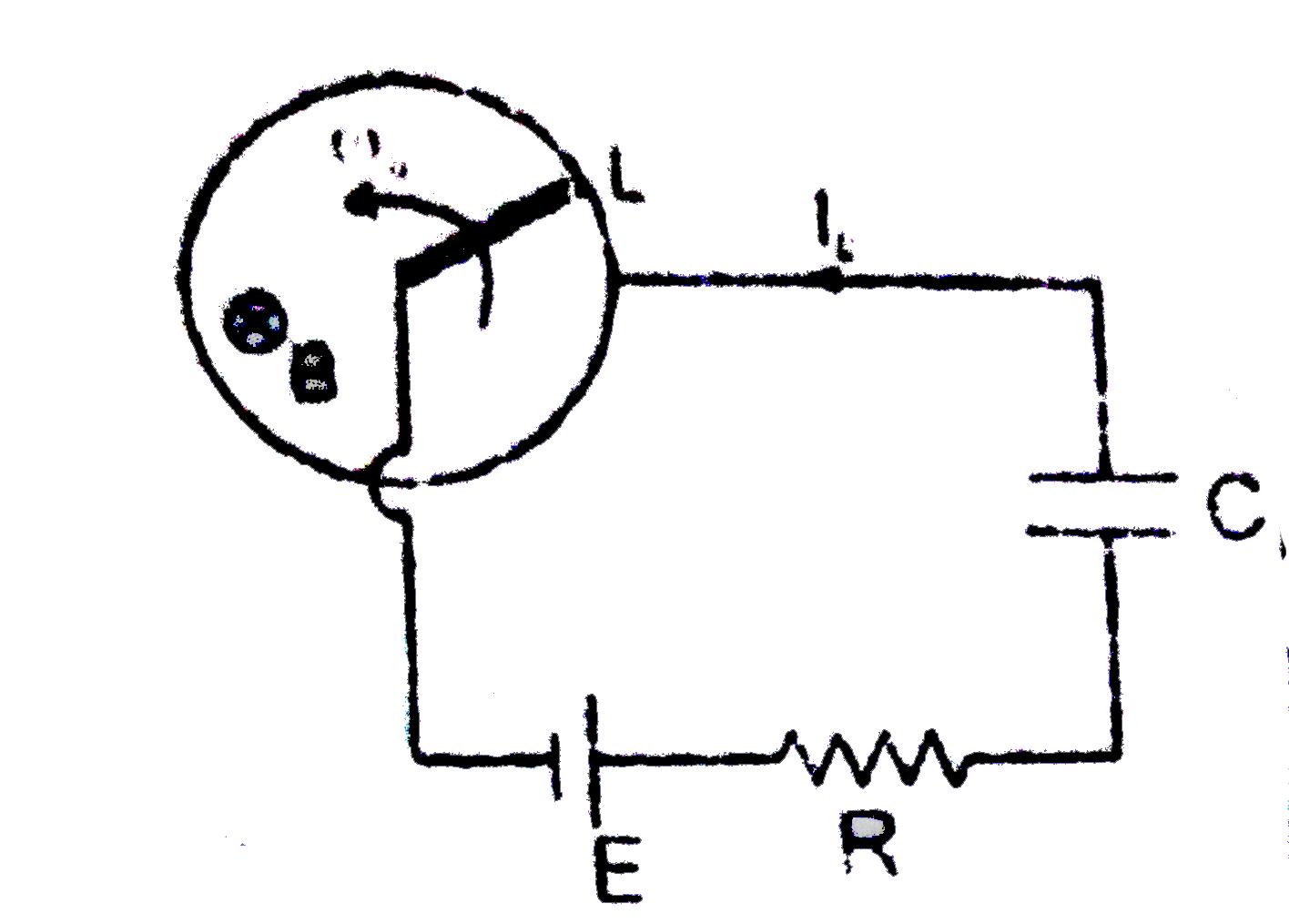
is a smooth conducting loop of radius & fixed in a horizontal plane.A conducting rod of mass and length slightly greater than higed at the centre of the loop can rotate in the horizontal plane such that the free end slides on the rim of the loop.There is a uniform magnetic field of strength directed vertically downward.The rod is rotated with angular velocity and left.The fixed end of the rod and the rim of the loop are connected through a battery of a resistance , and initially uncharged capacitor of capacitance in series.Find
(i)the time dependence of such that the current in the circuit is contant.
(ii)energy supplied by the battery by the time rod stops.
The correct Answer is:A, B, C, D
(i)The magnetic equivalent of the loop-rod system.
where =angular velocity of rod at any time then
applying loop law,
(ii) so .
Also energy supplied by battery
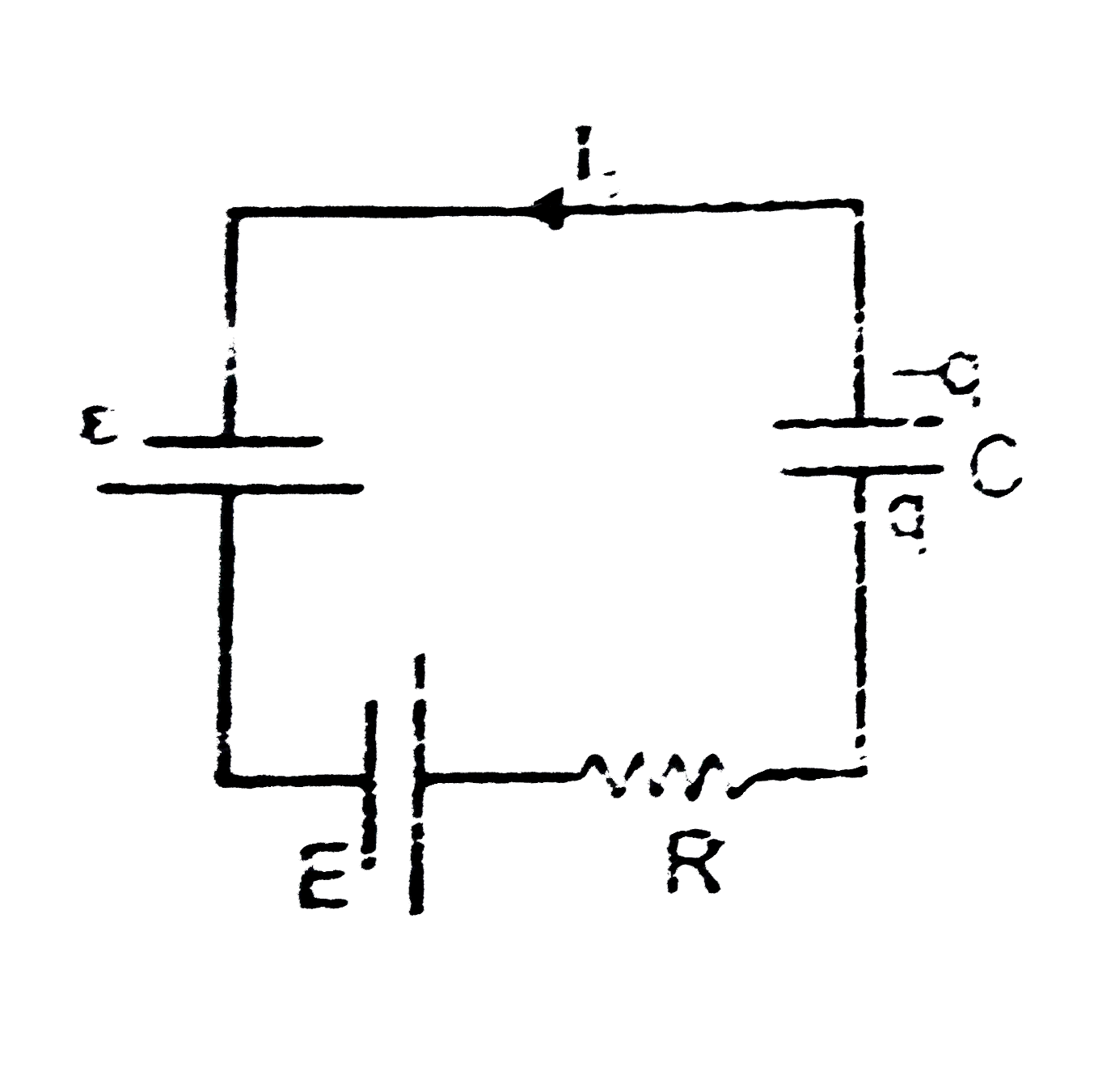
Topper's Solved these Questions
Similar Questions
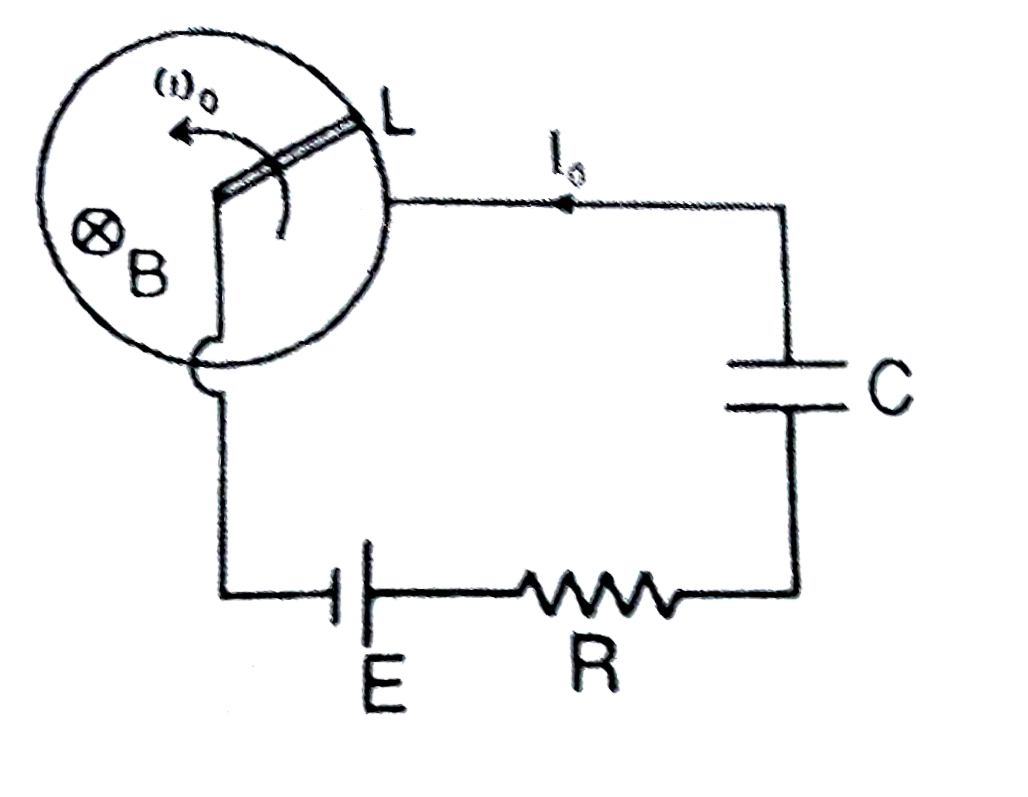
L is a smooth conducting loop of radius l=1.0 m & fixed in a horizontal plane. A conducting rod of mass m=1.0 kg and length slightly greater than l hinged at the centre of the loop can rotate in the horizontal plane such that the free end slide on the rim of the loop. There is a uniform magnetic field of strength B=1.0 T directed vertically downward. The rod is rotated with angular velocity ω0=1.0rad/s and left. The fixed end of the rod and the rim of the loop are connected through a battery of emf . E, a resistor of resistance R=1.0Ω, and intially uncharged capacitor of capacitance C=1.0 F in series. Find :
(i) the time dependence of emf . E such that the current I0=1.0A in the circuit is constant.
(ii) energy supplied by the battery by the time rod stops.
 View Solution
View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View Solution
Knowledge Check
- Question 1 - Select One
A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to L - Question 2 - Select One
A copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
ABωl2B12Bωl2C2Bωl2D14Bωl2 - Question 3 - Select One
A metallic rod of length 'l' is tied to a string of length 2l and made to rotate with angular speed w on a horizontal table with one end of the string fixed. If there is a vertical magnetic field 'B' in the region, the e.m.f. Induced across the ends of the rod is
 A2Bωl22B3Bωl22C4Bωl22D5Bωl22
A2Bωl22B3Bωl22C4Bωl22D5Bωl22
A loop PQR formed by three identical uniform conducting rods each of length a is suspended from one of its vertices (P) so that it can rotate about horizontal fixed smooth axis CD.Initially plane of loop is in vertical plane.A constant current i is flowing in the loop.Total mass of the loop is m At t=0,a uniform magnetic field of strength B directed vartically upwards is swiched on.Acceleration due to gravity is g then Find the minimum valeu of B so that the plane of the loop becomes horizontal (even for an instant)during its subsequent motion.
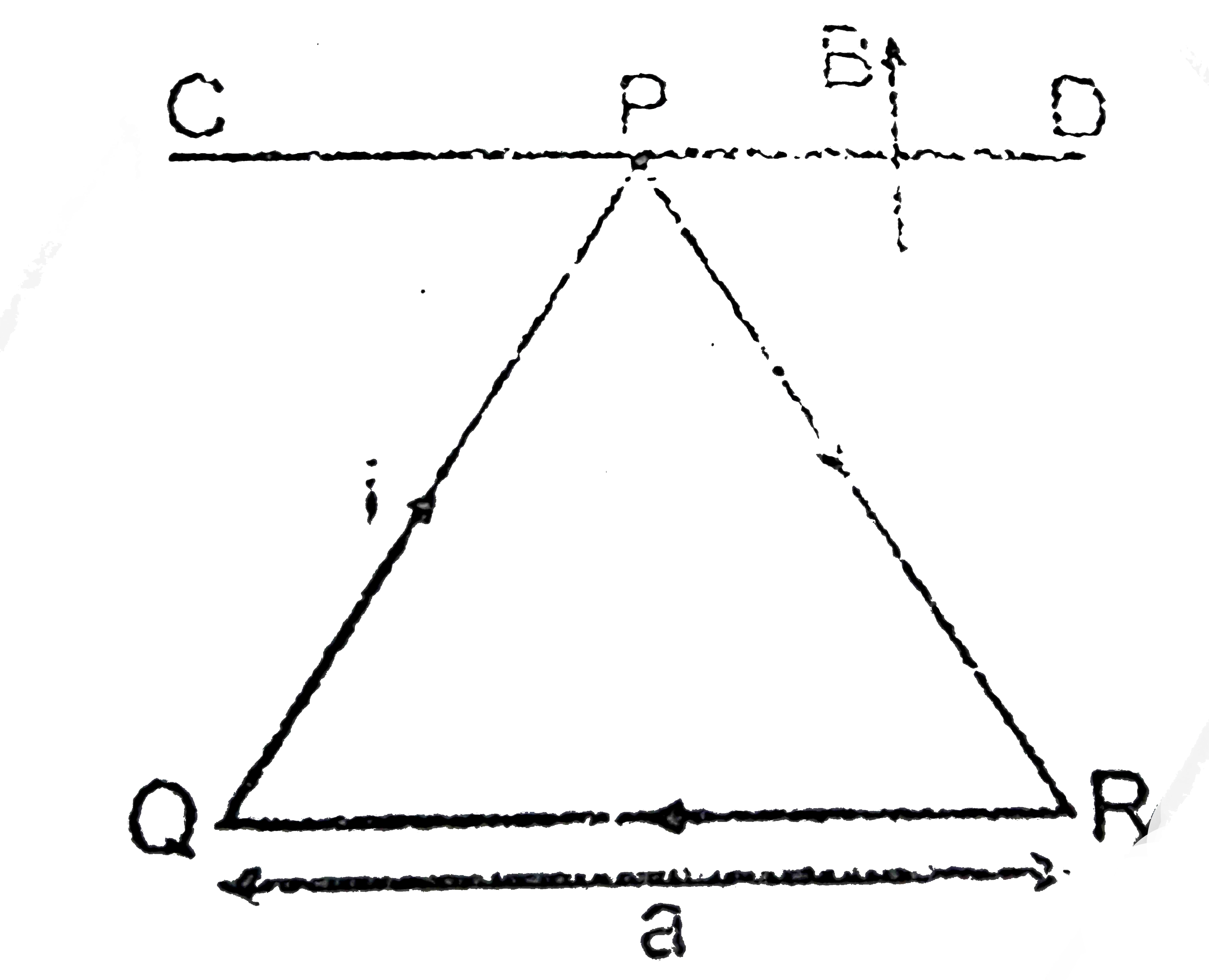 View Solution
View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :
 View Solution
View SolutionA rod of mass M and length L is placed on a smooth horizontal surface. It is hinged at one end so that it can rotate freely in a horizontal circle about this end. There exists a uniform magnetic field →B perpendicular, into the horizontal surface everywhere. The strength of magnetic field starts varying as B=B0t.
(i) Find the torque acting on the rod about its hinged end.
(ii) Find the reaction produced at hinge at t = 0.
(A charge Q is distributed uniformaly on the rod)View SolutionA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView Solution

