A thin wire ring of radius a and resitance $r$ is located inside a long solenoid is equal to $l$ , its cross-sectional radius , to $b$ . At a certain moment the solenoid was connected to a source of a constant voltage $V$ . The total resistance of the circuit is equal to $R$ . Assuming the the radial force acting per unit length of the ring.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$L = π μ_{0} N n b^{2} = π μ_{0} (n l) n b^{2} = μ_{0} n^{2} π b^{2} l$
$I = \frac{V}{R} (1 - e^{- R t / L})$ …(i)
Determine the induced current in the ring The flux associated with ring is $ϕ_{ρ} = B π a^{2} = μ_{0} n l π a^{2}$
Here $B$ =Magnetic field due to solenoid $= μ_{0} n l$
$∴$ Induced $e m f$ in the ring is $ε' = \frac{d ϕ_{r}}{d t} = μ_{0} n r a^{2} \frac{d l}{d t}$
$∴$ The current in the ring is $l' = \frac{ε'}{r} = \frac{μ_{0} n π a^{2}}{r} \frac{d i}{d t}$
From equ.(i) we get $l = \frac{V}{R} (1 - e^{- R t / L})$
$\frac{d i}{d t} = \frac{V}{L} e^{- R t / L}$
$l' = \frac{μ_{0} n π a^{2}}{r} \frac{V}{L} e^{- R t / L}$
Determine magnetic force on an element of length $d L$ of the ring The magnetic force on the considered element is $d F = l' d L B$
$∴$ Force per unit length is $F_{0} = \frac{d F}{d L} = I' B$
$∴$ On putting the value we get , $F_{0} = \frac{μ_{0} n π a^{2} V}{L r} e^{- R t / L} (μ_{0} n l)$
$= \frac{μ_{0}^{2} n^{2} π a^{2} V}{L r} e^{- R t / L} (1 - e^{- R t / L})$
For maximum value of $F_{0}, \frac{d F_{0}}{d t} = 0$
After solving, we $F_{0 max} = {(\frac{d F}{d L})}_{max} = \frac{μ_{0}^{2} a^{2} V^{2}}{4 r R l b^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

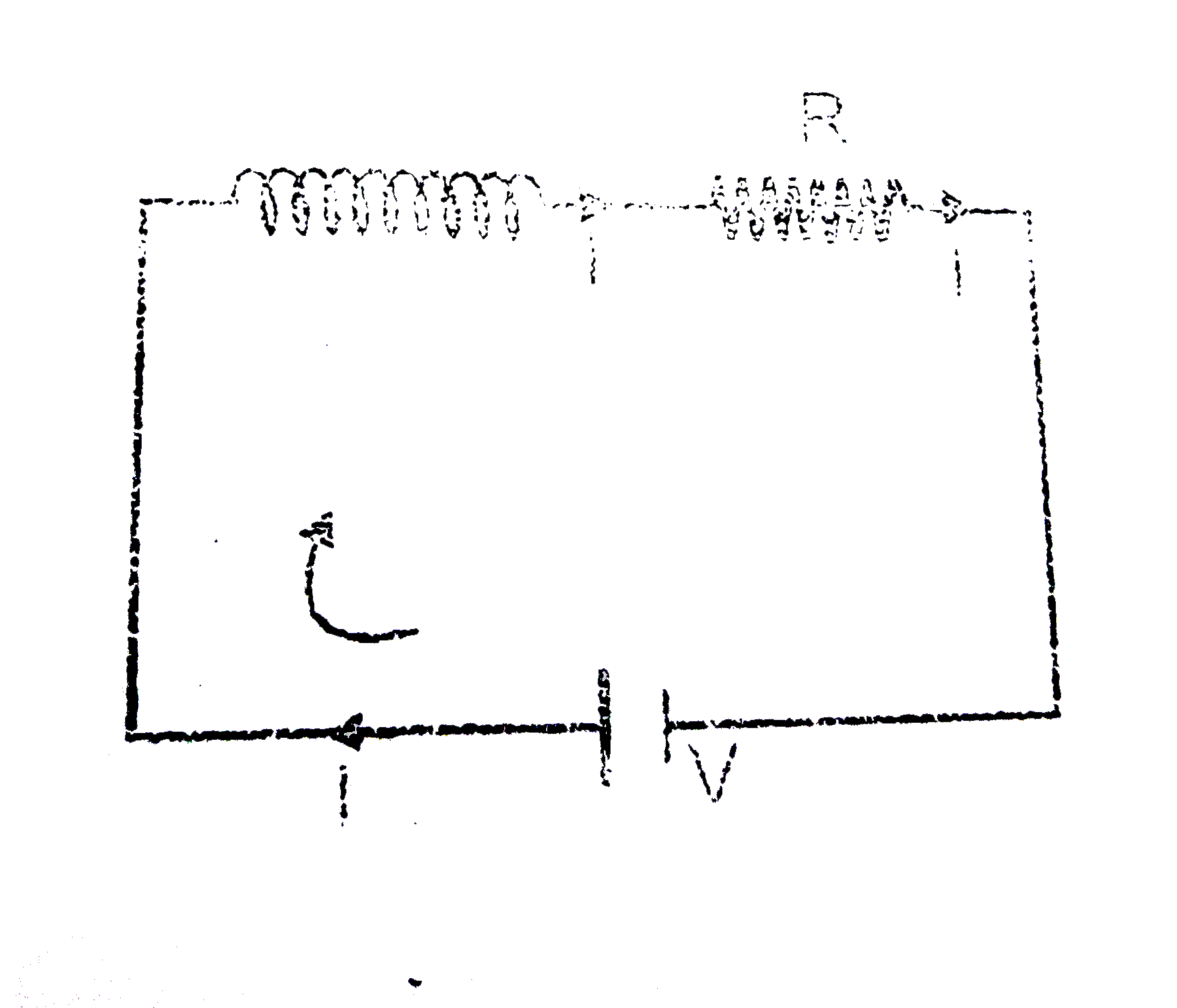
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A resistance $R_{1}$ is connected to a source of constant voltage . On connecting a resistance $R_{2}$ in series with $R_{1}$
AThe total thermal power dissipated increases
BThermal power dissipated by $R_{1}$ decreases
CThermal power dissipated by $R_{1}$ increases
DTotal power dissipiated decreases
Question 2 - Select One
A ring of area $A$ and resistance $R$ is placed on the axis of a solenoid. The mutual inductance between them is $M$ . When the current in the solenoid changes at the rate of $I$ , the magnetic moment of the ring is
A $A R M I$
B $A I / R M$
C $M R I / A$
D $A M I / R$
Question 3 - Select One
For a solenoid keeping the turn density constant its length makes halved and its cross section radius is doubled then the inductance of the solenoid increased by :-
A $200 %$
B $100 %$
C $800 %$
D $700 %$

RESONANCE-ELECTROMAGNETIC INDUCTION-A.l.P

Home
Ask Doubt
Profile