White coherent light (400nm−700nm) is sent through the slits of a Young's double slit experiment (as shown in the figure). The separation between the slits is 1mm and the screen is 100cm away from the slits. There is a hole in the screen at a point 1.5mm away (along the width of the fringes) from the central line. (a) For which wavelength (s) there will be minima at that point ? (b) which wavelength (s) will have a maximum intensity?

The correct Answer is:(a) 428nm,600nm,<br>(b)500 nm
As λ<<d,⇒β=λDd can be used
For minima
(a) y=(n+12)β.=(n+12)λDd
⇒λ=1.5×10−3×1×10−31×(n+12)=1.5×10−6n+12
n=1,λ=23×1.5×10−6=1000nm
n=2,λ=25×1.5×10−6=600nm
n=3,λ=27×1.5×10−6=428nm
Putting integral values of 'n'
n=1,λ=1000nm
n=2,λ=600nm.
n=3,λ=428nm
So only λ=428nmandλd=6000nm, will have minima at the hole. Hence they will be absent in the light coming out.
(b) 1.5mm=nβ.
1.5mm=n(λDd)
⇒λ=1.5×10−3×1×10−3n×100×102
for n=1.λ=1500nm.
for n=2.λ=750nm.
for n=3.λ=500nm.
Hence only λ=500nm will have maximum intensity.
Topper's Solved these Questions
Similar Questions
White coherent light (400nm−700nm) is sent through the slits of a YDSE. D=0.5mm, D=50 cm. There is a hole in the screen at a point 1.0mm away (along the width of the fringes) from the central line.
(a) Which wavelength will be absent in the light coming from the hole?
(b) Which wavelength(s) will have a strong intensity?

View SolutionWhite coheral light (400 nm 700 nm ) is sent through the slit of a Young.s double slit experiment. The separation between the slits is 0.5 mm and the screen is 50 away from the slits . There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. Which wavelengths (s) will be absent in the light coming from the hole ?
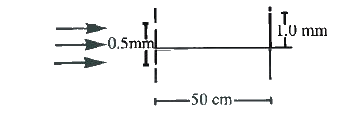
View Solution
Knowledge Check
In a double experiment, the distance between the slit is 1 mm and screen is 25 cm away from the slits. The wavelength of light is 6000Å. The width of the fringe on the screen is
A0.15 mmB0.24 mmC0.30 mmD0.12 mmIn a Young’s double slit experiment, the slit separation is 0.2cm, the distance between the screen and slit is 1 m . Wavelength of the light used is 5000Å. The distance between two consecutive dark fringes (in mm ) is
A2×10−5mB2×10−3mC0.2×10−3mDNone of these
White coherent light (400 nm- 700 nm) is sent through the slits of a young.s double slit experiment. The separation between the slits is 0.5mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1 mm from the centre.
In the above problem which wavelength have a strong intensity at the hole?
View SolutionWhite coherent light (400nm−700nm) is sent through the slits of a YDSE. d=0.5mm, D=50 cm. There is a hole in the screen at a point 1.0mm away (along the width of the fringes) from the central line.
(a) Which wavelength will be absent in the light coming from the hole?
(b) Which wavelength(s) will have a strong intensity?

View SolutionWhite coherent light (400nm−700nm) is sent through the slits of a YDSE. d=0.5mm, D=50 cm. There is a hole in the screen at a point 1.0mm away (along the width of the fringes) from the central line.
(a) Which wavelength will be absent in the light coming from the hole?
(b) Which wavelength(s) will have a strong intensity?

View SolutionWhite coherent light (400nm−700nm) is sent through the slits of a YDSE. D=0.5mm, D=50 cm. There is a hole in the screen at a point 1.0mm away (along the width of the fringes) from the central line.
(a) Which wavelength will be absent in the light coming from the hole?
(b) Which wavelength(s) will have a strong intensity?

View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View Solution
