Velocity of a particle moving in a straight line is v=sqrt(9+4s). Here

The displacement of a particle moving in a straight line, is given by $s = 2 t^{2} + 2 t + 4$ where $s$ is in metres and $t$ in seconds. The acceleration of the particle is.
A $2 m / s^{2}$
B $4 m / s^{2}$
C $6 m / s^{2}$
D $8 m / s^{2}$
For a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.

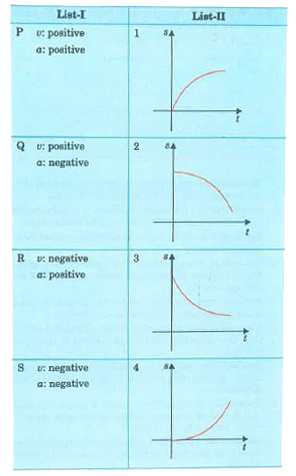A $\begin{matrix} P & Q & R & S 3 & 2 & 4 & 1 \end{matrix}$
B $\begin{matrix} P & Q & R & S 1 & 3 & 2 & 4 \end{matrix}$
C $\begin{matrix} P & Q & R & S 2 & 1 & 3 & 4 \end{matrix}$
D $\begin{matrix} P & Q & R & S 4 & 1 & 3 & 2 \end{matrix}$
A particle moving in a straight line has velocity-displacement equation as $v = 5 \sqrt{1 + s} .$ Here v is in $m s^{- 1}$ and s in metres. Select the correct alternative.
AParticle is initially at rest
BInitially velocity of the particle is $5 m / s$ and the particle has a constant acceleration of $12.5 m s^{- 2}$
CParticle moves with a uniform velocity
DNone of the above

Velocity of a particle moving in a straight line is $v = \sqrt{9 + 4 s}$ . Here v is in m/s and 's' displacement in meter. Mass of the particle is 2kg. The time in seconds at which average power is ${(\frac{3}{4})}^{t h}$ of the instantaneous power is :