A conical flask of mass 10 kg and base area is floating in liquid of specific gravity 1.2 as shown in figure. The force that liquid exerts on curved surface of conical flask is 10x newton (Neglect the atmospheric pressure and take g = 10 ) then the value of x is

The correct Answer is:2
By work energy theorem
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A liquid of mass 1 kg is filled in a flask as shown in figure. The force exerted by the flask on the liquid is (g=10m/s2) [Neglect atmospheric pressure]:
 A10 NBgreater than 10NCless than 10NDzero
A10 NBgreater than 10NCless than 10NDzero - Question 2 - Select One
A cubical block ofmass √310 kg and edge 20cm is placed on a rough horizontal surface as shown in the figure-5.126. A force of 1N is applied at one end of the block and the block remains stationary. The normal force exerted by the surface on the block acts (g=10m/s2)
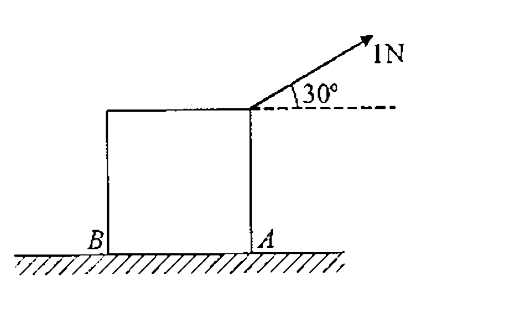 Athrought the centre of mass of the blockBthrough point BCthrough point ADthrough the point at the distance 5 m from A
Athrought the centre of mass of the blockBthrough point BCthrough point ADthrough the point at the distance 5 m from A - Question 3 - Select One
A block of mass √3/10kg is placed on a rough horizontal surface as shown in the figure. A force of 1N is applied at one end of the block and the block remains stationary. The normal force exerted by the sruface on the block acts(g=10m/s2)
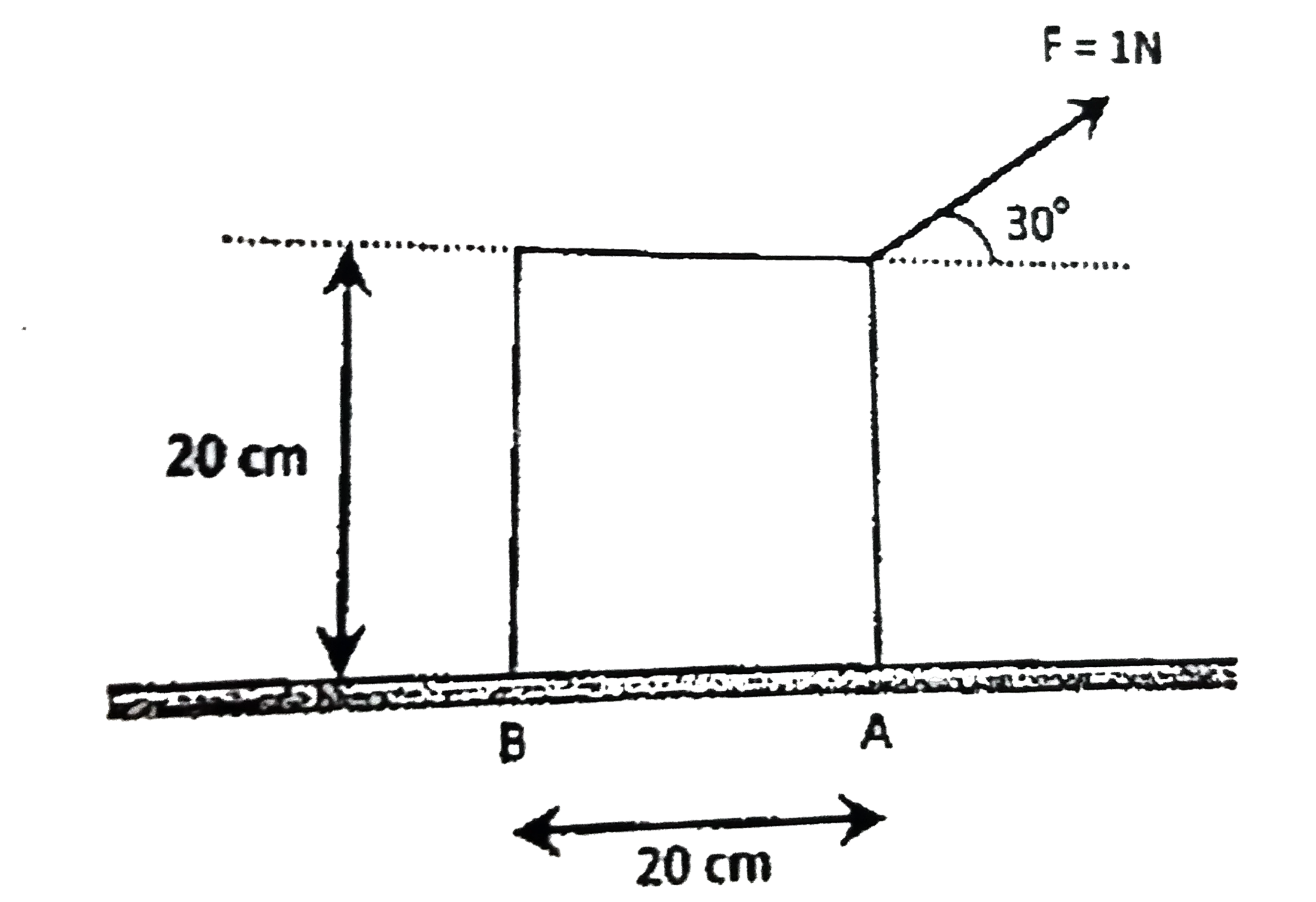 Athrough the center of mass of the blockBthrough point A.Cthrough point B.Dthrough the point at a distance 5cm. From A
Athrough the center of mass of the blockBthrough point A.Cthrough point B.Dthrough the point at a distance 5cm. From A
What is the absolute pressure on a swimmer 10m below the surface of a lake? Take atmospheric pressure 1×105N/m2
View SolutionA box of mass 10 kg has a base area of 1m2. What is the pressure exerted by it on the ground? (Take 1kg wt=10N)
View SolutionA block of mass 1 kg is released on wedge from position M as shown in figure (Neglect friction everywhere). The force exerted by vertical wall W on wedge, when the block is at position N is 152√P newton, then what is the value of P (Take g = 10 m/s2)?
 View Solution
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
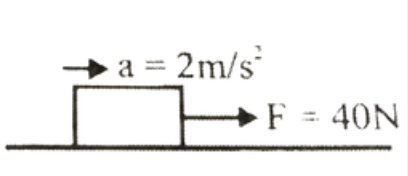 View Solution
View SolutionA 100 cm long wire of mass 40 g supports a mass of 1.6 kg as shown in figure . Find the fundamental frequency of the portion of the string between the wall and the pulley. Take g=10m/s2.
 View Solution
View Solution
