A tower subtends angles $α, 2 α, 3 α$ respectively, at point $A, B, a n d C$ all lying on a horizontal line through the foot of the tower. Prove that $\frac{A B}{B C} = 1 + 2 cos 2 α .$

A

$\frac{3 sin α}{sin 2 α}$

B

$1 + 2 {cos}^{2} α$

C

$2 + {cos}^{3} α$

D

$\frac{sin 2 α}{sin α}$

Video Solution

Text Solution

Verified by Experts

Let PM the tower .

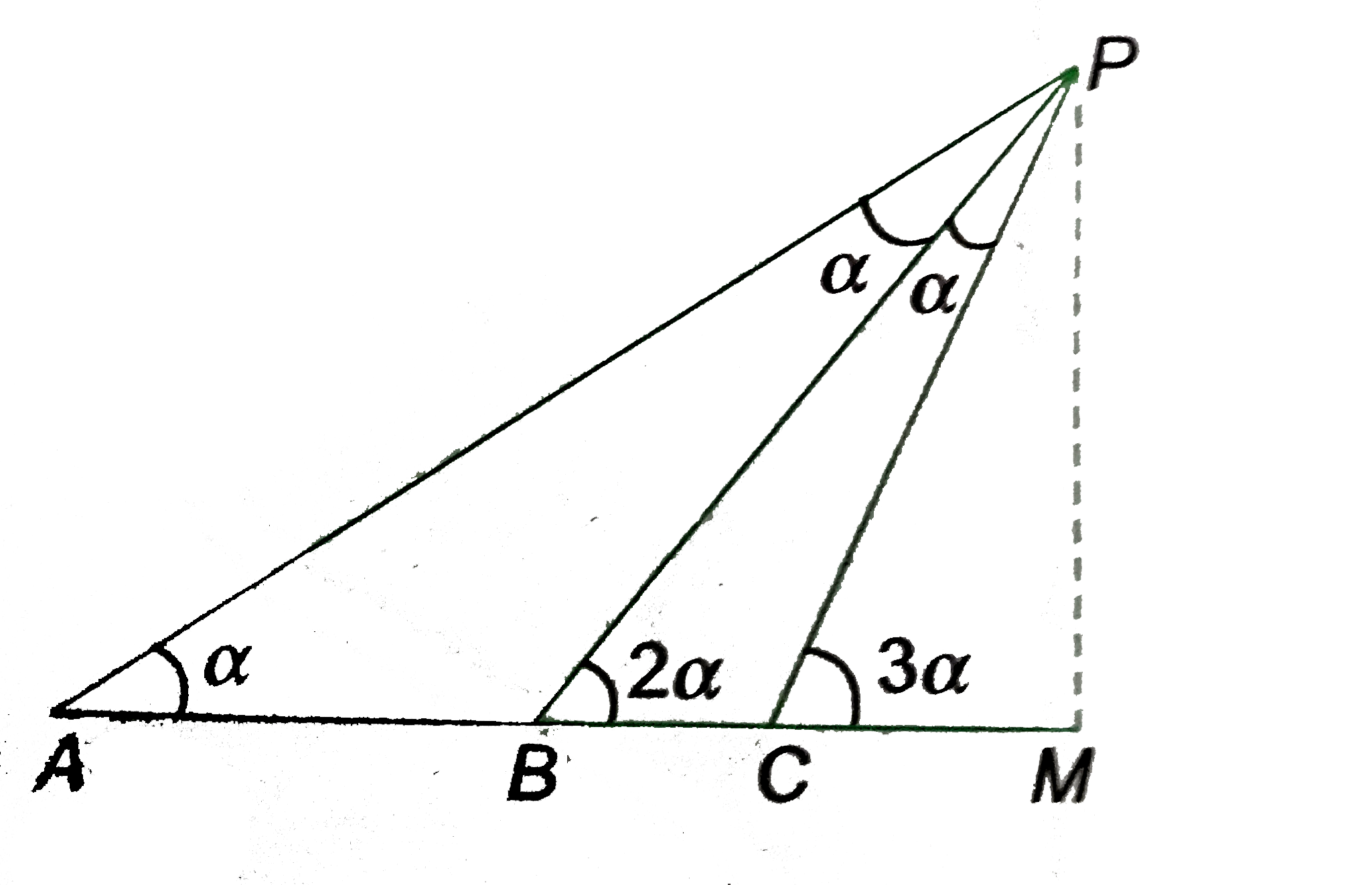
Given $∠ B A P = α, ∠ C B P = 2 α and ∠ M C P = 3 α$
$∴ ∠ A P B = ∠ P B C - ∠ B A P = 2 α - α = α$
Similarly, $∠ B P C = α$
$\Rightarrow B P = A B$
By sine formula in triangle BCP , we have
$\frac{B C}{sin (∠ B P C)} = \frac{B P}{sin (∠ B C P)}$
$\Rightarrow \frac{B C}{sin α} = \frac{A B}{sin (180^{\circ} - 3 α)}$
$\Rightarrow \frac{A B}{B C} = \frac{sin 3 α}{sin α} = \frac{3 sin α - 4 {sin}^{3} α}{sin α}$
$= 3 - 4 {sin}^{2} α$
$= 3 - 2 (1 - cos 2 α)$
$= 1 + 2 cos 2 α$

|

Updated on:21/07/2023

Class 12 MATHS HIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A tower subtends angles $α, 2 α and 3 α$ respectively at points, A, B and C (all points lying on the same side on a horizontal line through the foot of the tower), then the value of $\frac{A B}{B C}$ is equal to
A $1 + 2 cos 2 α$
B $1 - 2 cos 2 α$
C $1 + 3 cos 2 α$
D $1 - 3 cos 2 α$
Question 2 - Select One
A tower subtends angle $θ, 2 θ, 3 θ$ at the three points A,B and C respectively lying on a horizontal line through the foot of the tower. Then AB/BC is equal to
A $3 - 4 {sin}^{2} θ$
B $\frac{sin 3 θ}{sin 2 θ}$
C $\frac{sin 2 θ}{sin θ}$
D $\frac{sin 3 θ}{cos θ}$
Question 3 - Select One
A vertical tower OP of height h subtends angle $α, β, γ$ respectively at the point A, B, C on the horizontal plane through the foot O of the tower. A is due west of the tower. B is due east of A and on the same side of the tower as A. C is due south of B, then AC =
A $h (cot α - cot β)$
B $h \sqrt{{cot}^{2} γ - {cot}^{2} β}$
C $h \sqrt{{cot}^{2} α + {cot}^{2} γ - 2 cot α cot β}$
D $h \sqrt{{cot}^{2} γ + {cot}^{2} β - 2 cot α cot β}$

CENGAGE-HIGHT AND DISTANCE -Exercise

Home
Ask Doubt
Profile