A tower of height b subtends an angle α at a point on the same level as the food of the tower .At a second point , b meters above the first , the angle of depression of the foot pole and the finds that the elevation is now 2θ .The value of cot θ is
b cot α tan β
btanαtanβ
btanαcotβ
bcotαcotβ
Let AB be the tower of height h, D be the point x away fron B and C be another point b m above D
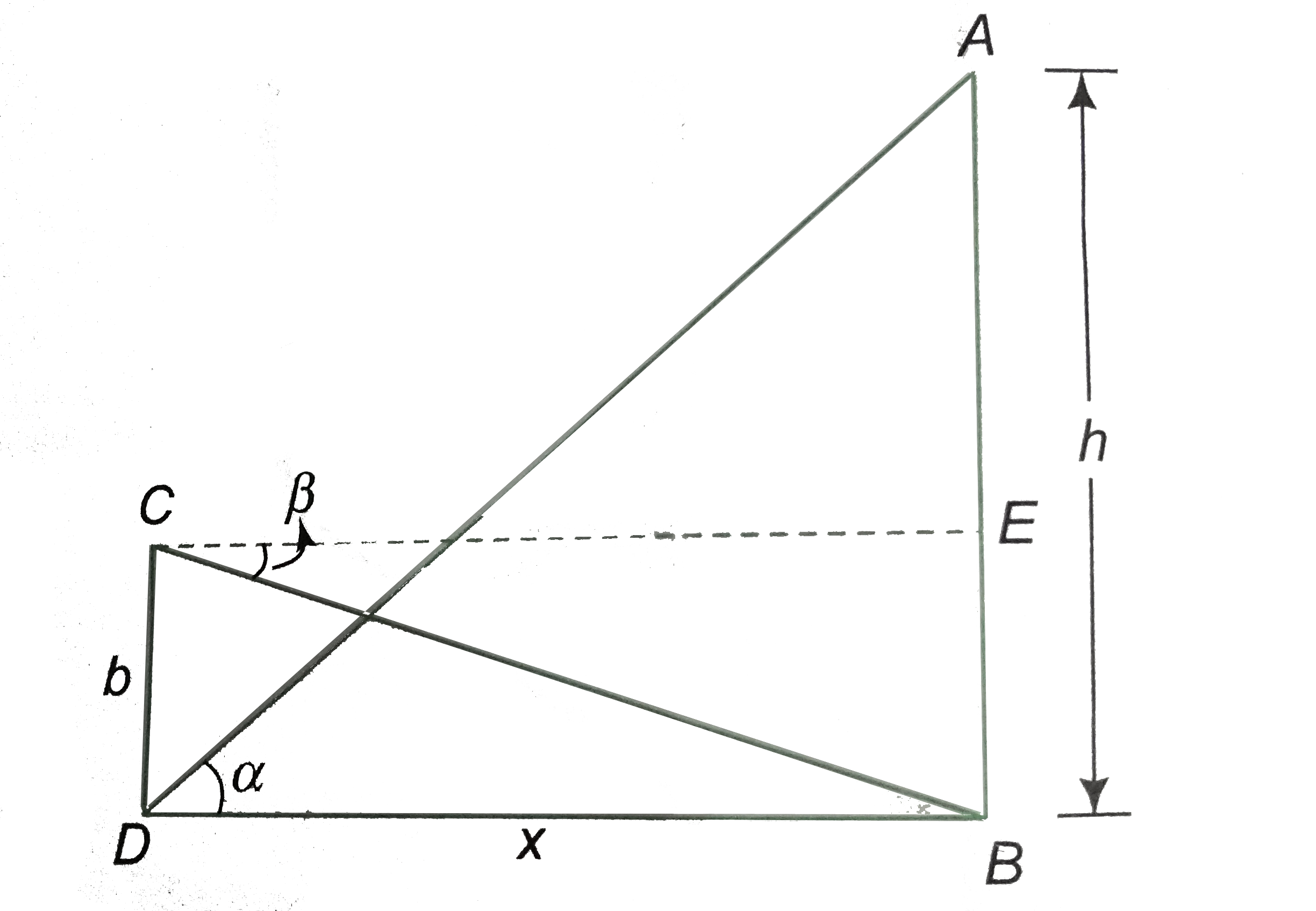
In triangle ABD.
h=xtanα
In triangle BCE. X=bcotβ
from (1) and (2) we get
∴h=btanαcotβ
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
A tower subtends an angle α at a point on the same level as the root of the tower and at a second point, b meters above the first, the angle of depression of the foot of the tower is β. The height of the tower is
View SolutionA tower subtends an angle 75∘ at a point on the same level as the foot of the tower and at another point, 10 meters above the first, the angle of depression of the foot of the tower is 15∘. The height of the tower is (in meters)
View Solution
Knowledge Check
A tower subtends an angle 75∘ at a point on the same level as the foot of the tower and at another point, 10 meters above the first, the angle of depression of the foot of the tower is 15∘. The height of the tower is (in meters)
A10(√3+1)2B10(√3−1)2C10(2+√3)2DNone of theseA tower subtends an angle of 60∘ at a point on the same level as the foot of the tower and at a second point just 10 meters above the first point the angle of depression of the foot of the tower is 15∘. The height of the tower is (in meters)
A10√3(2−√3)B10√3(2−√3)C10√3(2+√3)D10√3(2+√3)A tower subtends an angle of 30∘ at a point on the same level as the foot of the tower. At a second point h meter above the first, the depression of the foot of the tower is 60∘. The horizontal distance of the tower from the point is
Ah√3Bh3C3hD3hd
A tower subtends an angle of 30∘ at a point on the same level as the foot of the tower. At a second point h meter above the first, the depression of the foot of the tower is 60∘. The horizontal distance of the tower from the point is
View SolutionA tower subtends an angle of 30o at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60o. The height of the tower is
View SolutionA tower subtends an angle of 30∘ at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60∘ . The height of the tower is:
View SolutionA tower subtends an angle of 30∘ at a point on the same level as the foot of the tower. At a second point, h metre above first, point the depression of the foot of the tower is 60∘, the horizontal distance of the tower from the points is
View SolutionA tower subtends an angle of 30∘ at a point on the same level as the foot of the tower. At a second point h metre above the first, the depression of the foot of the tower is 60∘. The horizontal distance of the tower from the point is
View Solution
