Question

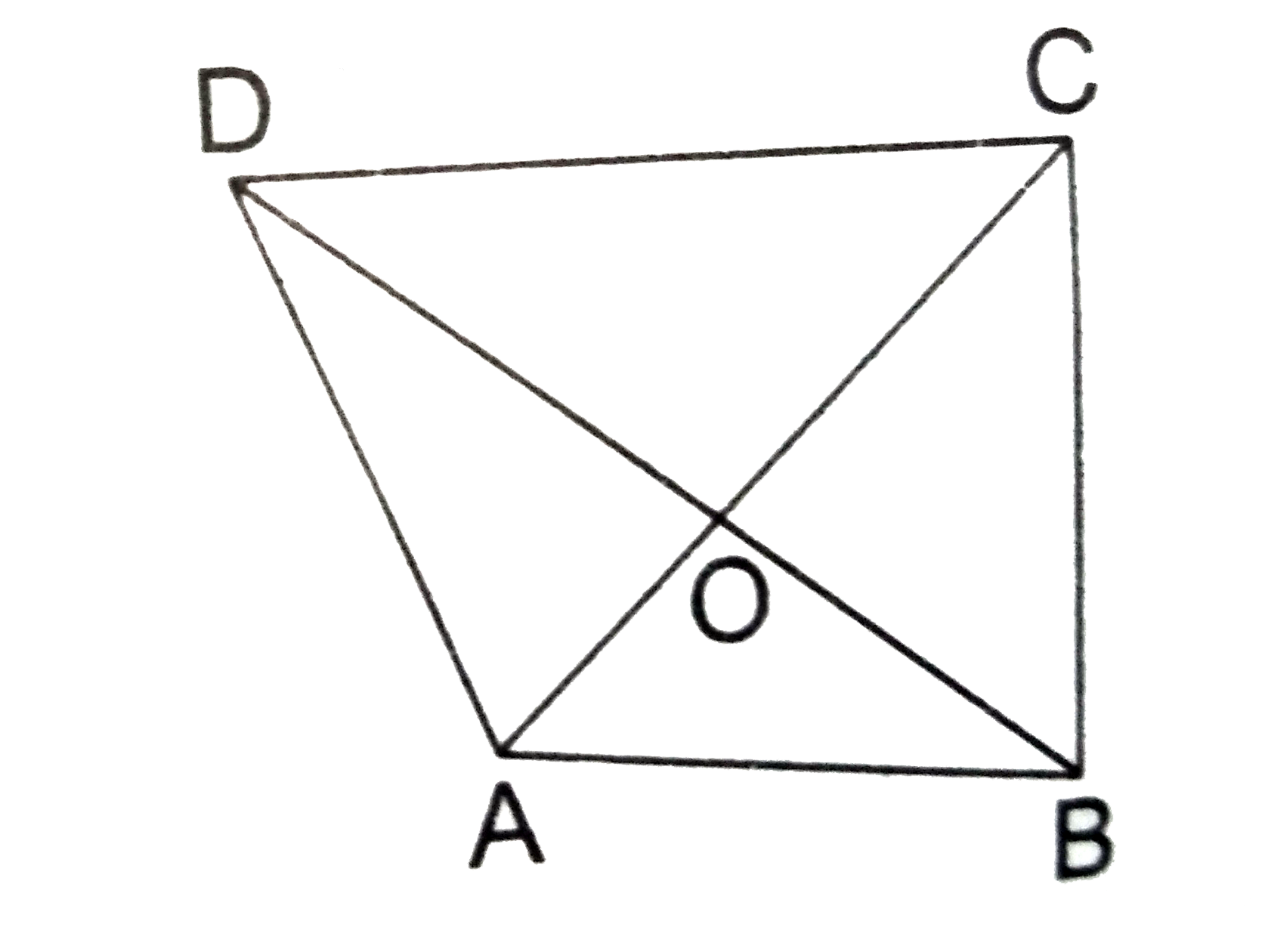
The diagonals of quadrilateral ABCD, AC and BD intersects at O. Prove that if BO = OD then the triangles ABC and ADC are equal in area.

Explanation

To prove that the areas of triangles ABC and ADC are equal given that BO = OD, we can follow these steps:

1. Given Information: We have a quadrilateral ABCD where the diagonals AC and BD intersect at point O. We are given that BO = OD.

2. Construction: Draw perpendiculars from points B and D to line AC. Let the foot of the perpendicular from B be point M and from D be point N.

3. Identify Angles: Since BM and DN are both perpendicular to AC, we have:
- ∠BMO = 90° (angle at M)
- ∠DNO = 90° (angle at N)

4. Vertically Opposite Angles: The angles ∠MOB and ∠NOD are vertically opposite angles, hence:
- ∠MOB = ∠NOD

5. Use Given Information: We know that BO = OD (given).

6. Triangles Comparison: Now we have two triangles, ΔBOM and ΔDON. We can compare these triangles:
- BO = OD (given)
- ∠BMO = ∠DNO = 90° (both are right angles)
- ∠MOB = ∠NOD (vertically opposite angles)

7. Congruence of Triangles: By the Angle-Angle-Side (AAS) criterion, we can conclude that:
- ΔBOM ≅ ΔDON

8. Corresponding Parts of Congruent Triangles: Since the triangles are congruent, their corresponding parts are equal. Thus:
- BM = DN (heights from B and D to line AC)

9. Area of Triangles: The area of triangle ABC can be expressed as:
\( \text{Area of } \triangle ABC = \frac{1}{2} \times AC \times BM \)
And the area of triangle ADC can be expressed as:
\( \text{Area of } \triangle ADC = \frac{1}{2} \times AC \times DN \)

10. Equating Areas: Since BM = DN (from the congruence of triangles):
\( \text{Area of } \triangle ABC = \text{Area of } \triangle ADC \)

11. Conclusion: Therefore, we have proved that the area of triangle ABC is equal to the area of triangle ADC.