If two bulbs of 25 W and 100 W rated at 200 volts are connected in series across a 440 volts supply, then
100 watt bulb will fuse
25 watt bulb will fuse
none of the bulb will fuse
both the bulbs will fuse
The correct Answer is:B
To solve the problem step by step, let's analyze the situation where two bulbs rated at 25 W and 100 W (both rated for 200 V) are connected in series across a 440 V supply. We need to determine which bulb will fuse.
Step 1: Calculate the Resistance of Each Bulb
The power P of a bulb is related to its voltage V and resistance R by the formula:
P=V2R
From this, we can rearrange to find the resistance:
R=V2P
For the 25 W bulb:
R1=200225=4000025=1600Ω
For the 100 W bulb:
R2=2002100=40000100=400Ω
Step 2: Calculate Total Resistance in Series
When resistors are in series, the total resistance Rt is the sum of the individual resistances:
Rt=R1+R2=1600Ω+400Ω=2000Ω
Step 3: Calculate the Current in the Circuit
Using Ohm's Law, we can find the current I flowing through the circuit when connected to a 440 V supply:
I=VRt=4402000=0.22A
Step 4: Calculate the Power Dissipated by Each Bulb
Now, we can calculate the power dissipated by each bulb using the formula:
P=I2R
For the 25 W bulb:
P1=I2R1=(0.22)2×1600=0.0484×1600=77.44W
For the 100 W bulb:
P2=I2R2=(0.22)2×400=0.0484×400=19.36W
Step 5: Compare Dissipated Power with Rated Power
Now we compare the power dissipated by each bulb with their rated power:
- The 25 W bulb is dissipating 77.44 W, which exceeds its rated power of 25 W. Therefore, the 25 W bulb will fuse.
- The 100 W bulb is dissipating 19.36 W, which is less than its rated power of 100 W. Therefore, the 100 W bulb will not fuse.
Conclusion
The 25 W bulb will fuse, while the 100 W bulb will not fuse.
---
The power P of a bulb is related to its voltage V and resistance R by the formula:
P=V2R
From this, we can rearrange to find the resistance:
R=V2P
R1=200225=4000025=1600Ω
R2=2002100=40000100=400Ω
When resistors are in series, the total resistance Rt is the sum of the individual resistances:
Rt=R1+R2=1600Ω+400Ω=2000Ω
Using Ohm's Law, we can find the current I flowing through the circuit when connected to a 440 V supply:
I=VRt=4402000=0.22A
Now, we can calculate the power dissipated by each bulb using the formula:
P=I2R
P1=I2R1=(0.22)2×1600=0.0484×1600=77.44W
P2=I2R2=(0.22)2×400=0.0484×400=19.36W
Now we compare the power dissipated by each bulb with their rated power:
- The 100 W bulb is dissipating 19.36 W, which is less than its rated power of 100 W. Therefore, the 100 W bulb will not fuse.
The 25 W bulb will fuse, while the 100 W bulb will not fuse.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
9 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension Based Type-1
3 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
10 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (NUMERICAL BASED QUESTIONS)
4 Videos
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assignment Problems (Objective) Level-II
15 Videos
Similar Questions
If two bulbs of 25Wand100W rated at 220V are connected in series across a 440V supply, will both the bulbs fuse ? If not which one ?
View SolutionIf two buibs of 25 W and 100 W rated at 400 V are connected in series across a440 V supply, will both the bulb fuse? If not, then which one ?
(b) Two bulbs rated at 60 W and 100 W (220 V) are connected (i) in series and (ii) in parallel. Find the heat dissipated in the bulbs and also the total heat dissipatedin the circuit.
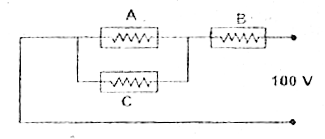
(c) A heater is designed to operate with a power of1000 watts in a 100 volt line. It is connected with an identical heater (B) in series and a100 V second heater (C) in parallel as shown. What should be the resistance of C so that the heater A may operate at a power level of 62.5 watts, if the entire combination is connected across a 100 V line
View Solution
Knowledge Check
If two bulbs of 25 W and 100 W, rated at 220 V, are connected in series across a 440 V supply
A25 W bulb will fuseB100 W bulb will fuseCnone will fuseDboth will fuseStatement-1: Two bulbs of 25W and 100W rated at 200V are connected in series across 200V supply. Ratio of powers of both the bulb in series is 2:1
Statement-2: In series current in both bulbs is same, therefore power depends on resistance of bulb.AStatement-1 is True,Statement-2 is True, Statement-2 is a correct explanation for Statement-1BStatement-1 is True,Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1CStatement -1 is True, Statement-2 is false.DStatement-1 is False, Statement-2 is True.If two bulbs of wattage 25 and 30, each rated at 220 volts , are connected in series with a 440 volt supply, which bulb will fuse
A25 W bulbB30 W bulbCNeither of themDBoth of them
A 25 watt, 220 volt bulb and a 100 watt, 220 volt bulb are connected in series across 440 volt line
View SolutionA 25 watt, 220 volt bulb and a 100 watt, 220 volt bulb are connected in series across 440 volt line
View SolutionWhat will happen when a 40 watt 220 volt lamp and 100 watt-220 volt lamp are connected in series across 40 volt supply?
View SolutionIf two bulbs of wattage 25 and 100 respectively each rated at 220 volt are connected in series with the supply of 440 volt , then which bulbs will fuse
View SolutionTwo bulbs of 100 W and 200 W working at 220 volt are joined in series with 220 volt supply. Total power consumed will be approximately.
View Solution
