The tangent to the curve y=ex drawn at the point (c,ec) intersects the line joining (c−1,ec−1)and(c+1,ec+1) (a) on the left of n=c (b) on the right of n=c (c) at no points (d) at all points
On the left of x=c
On the right of x=c
At no point
At all points
Slope of the tangent to y=ex at (c,ec) is given by
m1=(dydx)(c,ec)=ec
Therefore, the equation of the tangent at (1,e) is
y−e=e(x−1)
Also the slope of the line joining the points (c−1,ec−1)and(c+1,ec+1) is
m2=ec+1−ec−1(c+1)−(c−1)
=ec+1−ec−12
=ec(e−e−12)
We observe m2>m1
Thus, the tangent to the curve y=ex will intersect the given line to the left of the line x=c as shown in the following figure.
Hence the correct answer is (a).
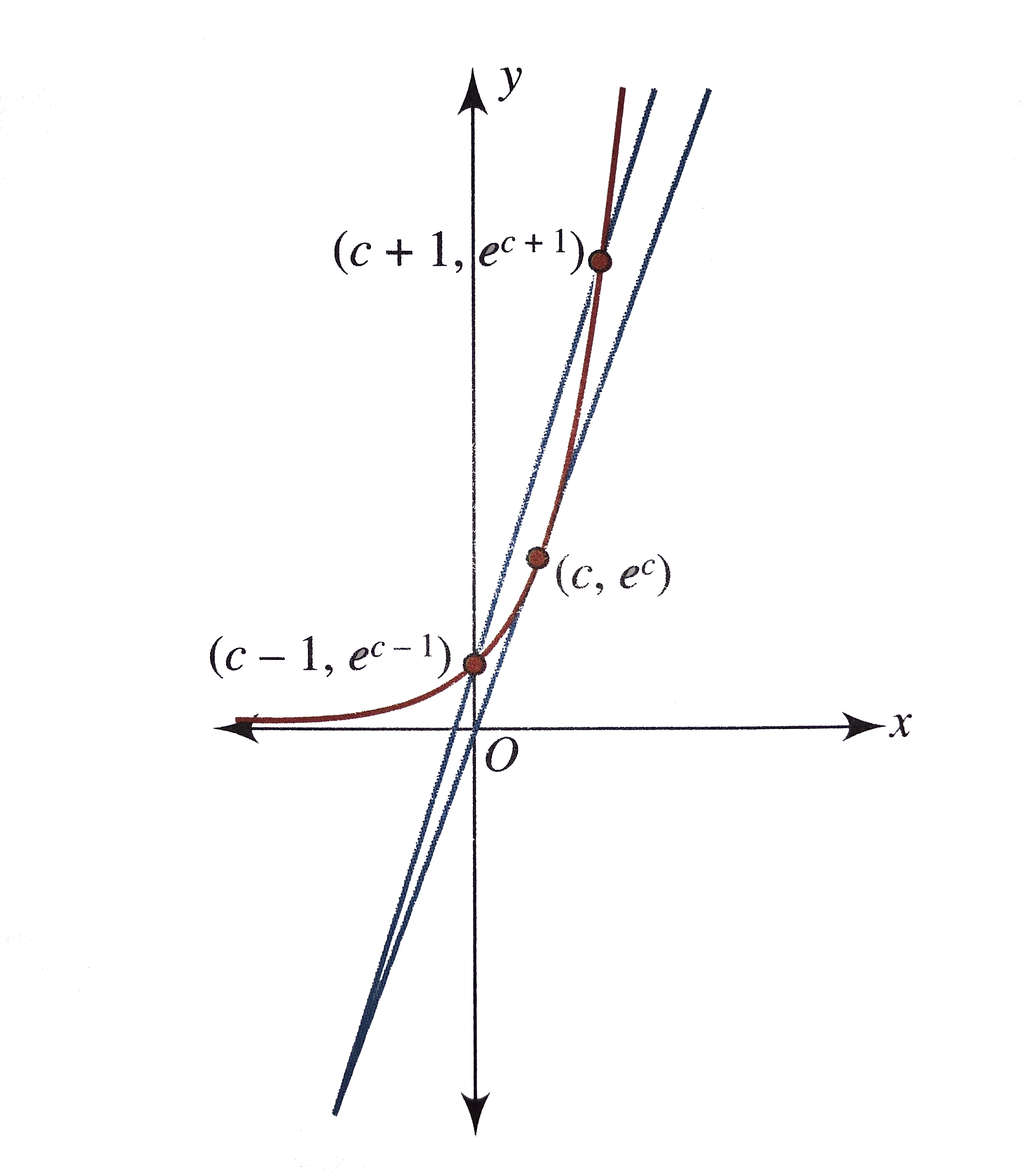
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
Similar Questions
If the tangent to the curve , y =f (x)= xlogex,(x>0) at a point (c, f(c)) is parallel to the line - segment joining the point (1,0) and (e,e) then c is equal to :
View SolutionIf the tangent to the curve y=ex at a point (c,ec) and the normal to the parabola, y2=4x at the point (1,2) intersect at the same point on the x-axis then the value of c is ____________.
View Solution
Knowledge Check
The tangent to the curve y=ex drawn at the point (c,ec) intersects the line joining the points (c−1,ec−1) and (c+1,ec+1)
Aon the left of x=cBon the right of x=0Cat no pointDat all pointsIf the joining the points (0,3) and (5,-2) is a tangent to the curve y=cX+1, then value of c is -
A1B-2C4D-4Five boys A, B, C, D, E are in a row. A is on the right of B, E is on the left of B but on the right of C and A is on the left of D. Who is second from the left?
ADBACEDB
The line joining the points (0,3) and (5,-2) becomes tangent to the curve y=cx+1 then c=
View SolutionWhen the tangent to the curve y=xlogx is parallel to the chord joining the points (1, 0) and (e, e) , the value of x is e1/1−e (b) e(e−1)(2e−1) (c) e2e−1e−1 (d) e−1e
View SolutionIf the line joining the points (0,3)and(5,−2) is a tangent to the curve y=Cx+1 , then the value of c is 1 (b) −2 (c) 4 (d) none of these
View SolutionFind value of c such that line joining points (0, 3) and (5, -2) becomes tangent to y=cx+1.
View SolutionFind value of c such that line joining the points (0, 3) and (5, -2) is a tangent to curve y=c/(x+1)
View Solution