The straight line 3x+4y−12=0 meets the coordinate axes at AandB . An equilateral triangle ABC is constructed. The possible coordinates of vertex C (2(1−3√34),32(1−4√3)) (−2(1+√3),32(1−√3)) (2(1+√3),32(1+√3)) (2(1+3√34),32(1+4√3))

A

(2(1−3√34),32(1−4√3))

B

(−2(1+√3),32(1−√3))

C

(2(1+√3),32(1+√3))

D

(2(1+3√34),32(1+4√3))

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A, D

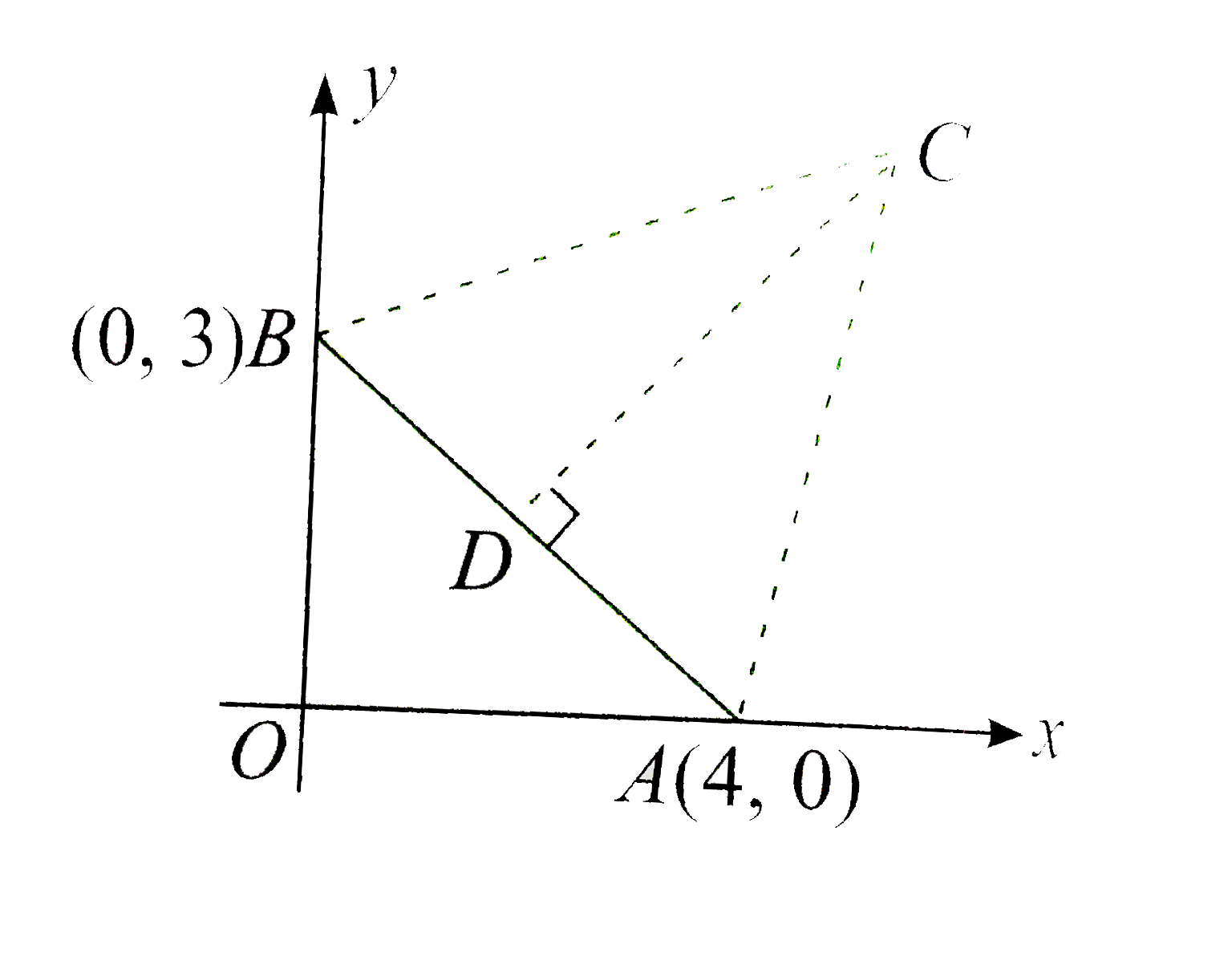
ocr_image
AB =5, D≡(2,32)
CD=5×√32=5√32
Slope of AB=−34
Slope of CD =34
If C≡(h,k),then
h−23/5=k−3/24/5=±5√32
or h=2(1−3√34),k=32(1−4√3)
or h=2(1+3√34),k=32(1+4√3)

Updated on:21/07/2023
|
Class 12MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The value of 2+√32−√3+2−√32+√3+√3+1√3−1 is

    A16+√3
    B4−√3
    C2−√3
    D2+√3

  • The value of 2+√32−√3+2−√32+√3+√3+1√3−1 is

    Aa) 16+√3
    Bb) 4−√3
    Cc) 2−√3
    Dd) 2+√3

  • (2+√32−√3+2−√32+√3+√3−1√3+1) simplifies to :

    A2−√3
    B2+√3
    C16−√3
    D40−√3