Question

If $x-2y+4=0and2x+y-5=0$
are the sides of an isosceles triangle having area $10sq\stackrel{.}{u}nits$
, the equation of the third side is
$3x-y=-9$
(b) $3x-y+11=0$

$x-3y=19$
(d) $3x-y+15=0$

Options

A. x+3y=-1
B. x+3y=19
C. 3x-y=-9
D. 3x-y=11

Answer

A::B::C::D

Explanation

Given lines are mutually perpendicular and intersect at `A((6)/(5), (13)/(5))`.

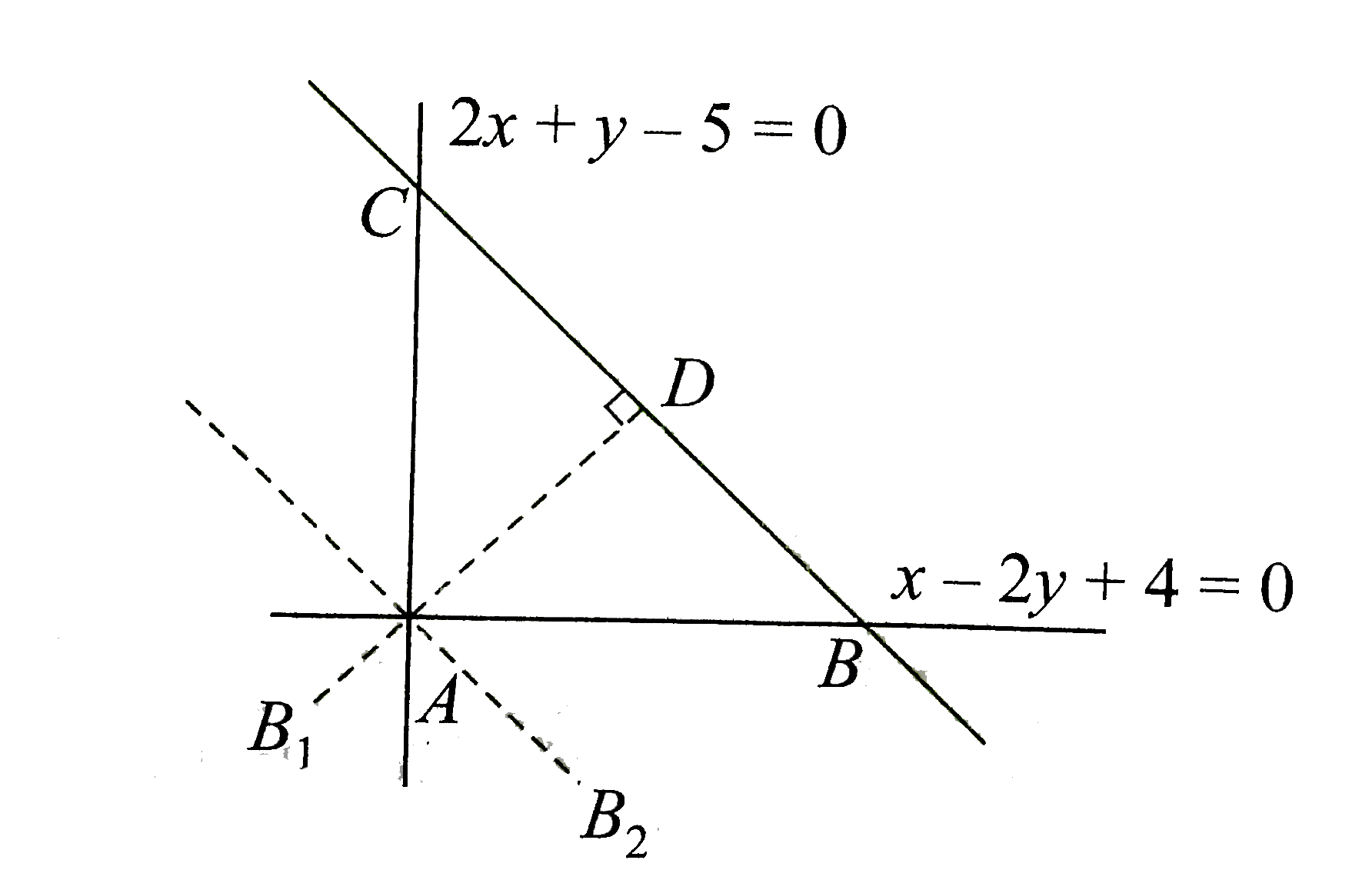
Equation of angle bisectors `B_(1) " and " B_(2)` of the given lines are
`x-2y+4 =+-(2x+y-5)`
or x+3y=9 and 3x-y=1
Side BC will be parallel to these bisectors
Let AD = a.
`therefore AB = asqrt(2)`
`"Area of triangle " ABC = (1)/(2) xx (asqrt(2))^(2) = a^(2)`
`therefore a^(2) = 10 " " ("Given")`
`"or " a = sqrt(10)`
Let equations of BC be `x+3y = lambda. "Then"`
`sqrt(10) = (|(18)/(5) - (13)/(5) - lambda|)/(sqrt(10))`
`lambda = -9, 11`
Therefore, equation of BC is 3x-y=-9 or 3x-y = 11