Question

Equation(s) of the straight line(s), inclined at ${30}^0$
to the x-axis such that the length of its (each of their) line
segment(s) between the coordinate axes is 10 units, is (are)
$x+\sqrt{3}y+5\sqrt{3}=0$

$x-\sqrt{3}y+5\sqrt{3}=0$

$x+\sqrt{3}y-5\sqrt{3}=0$

$x-\sqrt{3}y-5\sqrt{3}=0$

Options

A. `x+sqrt(3)y+5sqrt(3)=0`
B. `x-sqrt(3)y+5sqrt(3)=0`
C. `x+sqrt(3)y-5sqrt(3)=0`
D. `x-sqrt(3)y-5sqrt(3)=0`

Answer

B::D

Explanation

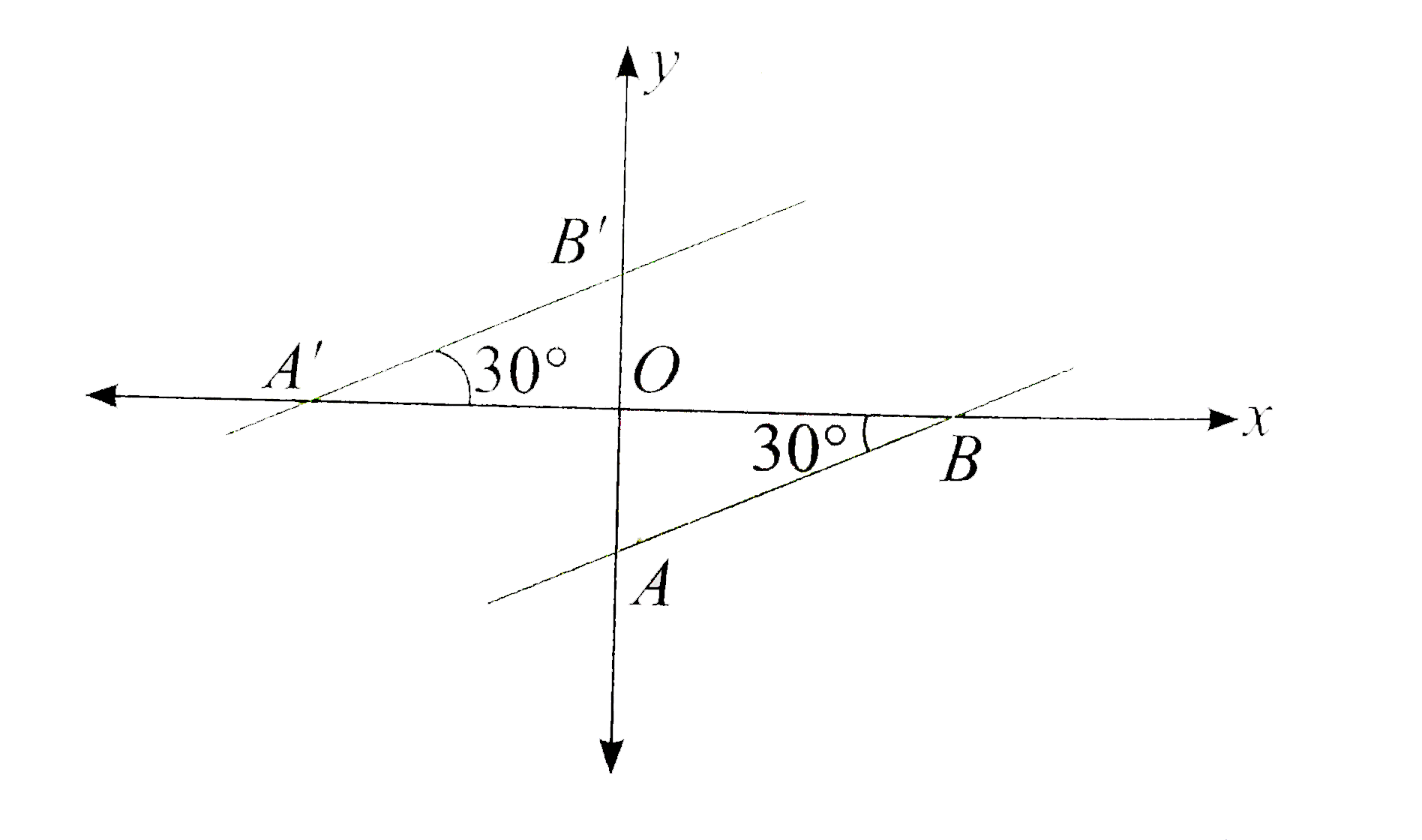
According to the question, AB=10. So, OA=10 `"sin"30^(@) =5`. Then the equation of line is
`y=(1)/(sqrt(3)) x +-5`
`"or " x-sqrt(3)y+-5sqrt(3)=0`