A bullet of mass m passes through a pendulum bob of mass M with velocity v and comes out of it with a velocity v2. The minimum value of v so that the bob completes one revolution in the vertical circle is (l = length of pendulum)
Mm√2gl
2Mm√2lg
2Mm√5lg
Mm√5lg
The correct Answer is:C
To solve the problem, we need to analyze the situation step-by-step:
Step 1: Understand the situation
A bullet of mass m passes through a pendulum bob of mass M with an initial velocity v and exits with a velocity of v2. We need to find the minimum value of v such that the pendulum bob can complete a full revolution in a vertical circle of radius l.
Step 2: Apply conservation of momentum
When the bullet passes through the bob, we can apply the principle of conservation of momentum. The momentum before the bullet enters the bob is equal to the momentum after it exits.
- Initial momentum: mv (bullet) + 0 (bob) = mv
- Final momentum: m⋅v2 (bullet) + M⋅u (bob)
Setting these equal gives us:
mv=m⋅v2+Mu
Step 3: Solve for u
Rearranging the equation:
mv−m⋅v2=Mu
mv2=Mu
u=mv2M
Step 4: Determine the minimum velocity u for the bob to complete a vertical circle
For the bob to complete a vertical circle, at the top of the circle, the tension in the string can be zero. The only force providing the centripetal force is the weight of the bob.
Using the centripetal force equation at the top of the circle:
Mg=Mv′2l
Where v′ is the velocity of the bob at the top of the circle.
From this, we can express v′:
v′2=gl
v′=√gl
Step 5: Apply conservation of energy
Using conservation of energy from the lowest point to the highest point:
Initial kinetic energy+Initial potential energy=Final kinetic energy+Final potential energy
12Mu2+0=12Mv′2+Mg(2l)
Substituting v′=√gl:
12Mu2=12M(gl)+Mg(2l)
12Mu2=12Mgl+2Mgl
12Mu2=52Mgl
u2=5gl
u=√5gl
Step 6: Substitute u back to find v
Now substituting u back into the equation for v:
u=mv2M
√5gl=mv2M
v=2Mm√5gl
Final Result
Thus, the minimum value of v required for the bob to complete one full revolution in the vertical circle is:
v=2Mm√5gl
A bullet of mass m passes through a pendulum bob of mass M with an initial velocity v and exits with a velocity of v2. We need to find the minimum value of v such that the pendulum bob can complete a full revolution in a vertical circle of radius l.
When the bullet passes through the bob, we can apply the principle of conservation of momentum. The momentum before the bullet enters the bob is equal to the momentum after it exits.
- Final momentum: m⋅v2 (bullet) + M⋅u (bob)
mv=m⋅v2+Mu
Rearranging the equation:
mv−m⋅v2=Mu
mv2=Mu
u=mv2M
For the bob to complete a vertical circle, at the top of the circle, the tension in the string can be zero. The only force providing the centripetal force is the weight of the bob.
Mg=Mv′2l
Where v′ is the velocity of the bob at the top of the circle.
v′2=gl
v′=√gl
Using conservation of energy from the lowest point to the highest point:
Initial kinetic energy+Initial potential energy=Final kinetic energy+Final potential energy
12Mu2+0=12Mv′2+Mg(2l)
12Mu2=12M(gl)+Mg(2l)
12Mu2=12Mgl+2Mgl
12Mu2=52Mgl
u2=5gl
u=√5gl
Now substituting u back into the equation for v:
u=mv2M
√5gl=mv2M
v=2Mm√5gl
Thus, the minimum value of v required for the bob to complete one full revolution in the vertical circle is:
v=2Mm√5gl
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
67 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
39 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
14 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A bullet of mass m strikes a pendulum bob of mass 2m with velocity u es shown in figure. If passes through and emerges but with a velocity u/2 from bob. The length of the pendulum bob is l=2m. If the minimum value of u for which the pendulum bob completes full circle is 10Xm/s, then find X.
(Take g=10m/s2)

View SolutionA pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that time
View Solution
Knowledge Check
A bullet of mass m strikes a pendulum bob of mass M with velocity u. It passes through and emerges out with a velocity u/2 from bob. The length of the pendulum is l. What should be the minimum value of u if the pendulum bob will swing through a complete circle?
A2Mm×√5glBM2m√5glC2Mm×1√5glDM2m×1√5glA bullet of mass m is being fired from a stationary gun of mass M. If the velocity of the bullet is v, the velocity of the gun is-
AMvm+MBmvMC(M+m)vMDM+mMvA bullet of mass m is fired with velocity v in a large bulk of mass M. The final velocity v' will be
AMvm+MBmvm+MC(m+M)vmD(m+M)v
A pendulum of string length l = 2m and bob of mass M Is hit by a bullet with initial velocity u which completely penetrates through it and leaves the bob with velocity 3u4. If M100 is the mass of bullet, then the minimum initial velocity of bullet to make the bob to complete vertical circle is......m/s (g=10m/s2)
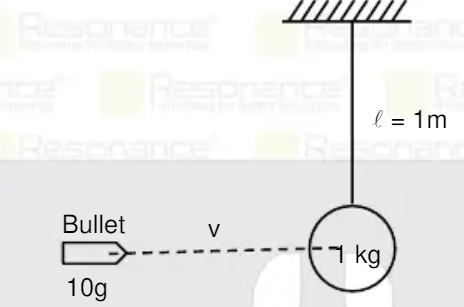
View SolutionA bullet of mass 10g travelling with velocity v collides with pendulum mass system of mass 1kg and length 1m and embedded in it as shown. Find minimum value of v so that pendulum mass undergoes complete circular motion.
View SolutionA bullet of mass m is fired with velocity v in a large bulk of mass M. The final velocity v' will be
View SolutionA pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
View SolutionA pendulum consists of a wooden bob of mass in and of length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed (v1)/3 and the bob just completes motion along a vertical circle. Then v1is
View Solution
