Two identical balls each moving with speed v at right angle to each other collide perfectly inelastically. Their speed after collision is
v
sqrt2v
v2
v√2
The correct Answer is:D
To solve the problem of finding the speed of two identical balls after a perfectly inelastic collision, we can follow these steps:
1. Understanding the Problem:
We have two identical balls, each with mass m, moving at right angles to each other with speed v. One ball is moving along the x-axis, and the other is moving along the y-axis.
2. Setting Up the Momentum Conservation:
Since the collision is perfectly inelastic, the two balls stick together after the collision. We will use the principle of conservation of linear momentum, which states that the total momentum before the collision is equal to the total momentum after the collision.
3. Calculating Initial Momentum:
- The momentum of the first ball moving along the x-axis is:
Momentumx=mv^i
- The momentum of the second ball moving along the y-axis is:
Momentumy=mv^j
- Therefore, the total initial momentum →Pinitial is:
→Pinitial=mv^i+mv^j
4. Calculating Final Momentum:
After the collision, the two balls combine to form a single object with mass 2m. Let the velocity of this combined mass be →V. The total final momentum →Pfinal is:
→Pfinal=2m→V
5. Applying Conservation of Momentum:
By conservation of momentum:
→Pinitial=→Pfinal
Thus, we have:
mv^i+mv^j=2m→V
6. Solving for Velocity →V:
Dividing both sides by 2m:
→V=12(v^i+v^j)=v2^i+v2^j
7. Finding the Magnitude of →V:
The magnitude of the velocity V can be calculated using the Pythagorean theorem:
V=√(v2)2+(v2)2=√v24+v24=√2v24=√v22=v√2
8. Conclusion:
The speed of the combined mass after the collision is:
V=v√2
Final Answer:
The speed of the two identical balls after the collision is v√2.
We have two identical balls, each with mass m, moving at right angles to each other with speed v. One ball is moving along the x-axis, and the other is moving along the y-axis.
Since the collision is perfectly inelastic, the two balls stick together after the collision. We will use the principle of conservation of linear momentum, which states that the total momentum before the collision is equal to the total momentum after the collision.
- The momentum of the first ball moving along the x-axis is:
Momentumx=mv^i
- The momentum of the second ball moving along the y-axis is:
Momentumy=mv^j
- Therefore, the total initial momentum →Pinitial is:
→Pinitial=mv^i+mv^j
After the collision, the two balls combine to form a single object with mass 2m. Let the velocity of this combined mass be →V. The total final momentum →Pfinal is:
→Pfinal=2m→V
By conservation of momentum:
→Pinitial=→Pfinal
Thus, we have:
mv^i+mv^j=2m→V
Dividing both sides by 2m:
→V=12(v^i+v^j)=v2^i+v2^j
The magnitude of the velocity V can be calculated using the Pythagorean theorem:
V=√(v2)2+(v2)2=√v24+v24=√2v24=√v22=v√2
The speed of the combined mass after the collision is:
V=v√2
The speed of the two identical balls after the collision is v√2.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - A)
Explore 67 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - B)
Explore 39 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-J (AAKASH CHALLENGERS QUESTIONS)
Explore 14 Videos
- WAVESBook:AAKASH INSTITUTEChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
Two particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collision
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Find the angle with the horizontal to which the particles move after collision.
View Solution
Knowledge Check
Two identical mass M moving with velocity u1andu2 collide perfectly inelastically. The loss in kinetic energy is
AM2(u2−u1)2BM2(u21−u22)CM4(u2−u1)2DM4(u21−u22)Two identical balls moving in opposite directions with speed 20 m/s and 25 m/s undergo head on perfectly inelastic collision. The speed of combined mass after collision is
A20 m/sB22.5 m/sC25 m/sD2.5 m/sTwo identical balls moving in opposite direction with speed 20 m/s and 25 m/s undergo head on perfectly inelastic collision. The spped of combined mass after collision is
A20msB22.5msC25msD2.5ms
Two particles of mass 2m and m moving with speed v and 2v respectively perpendicular to each other collides perfectly inelastically, then
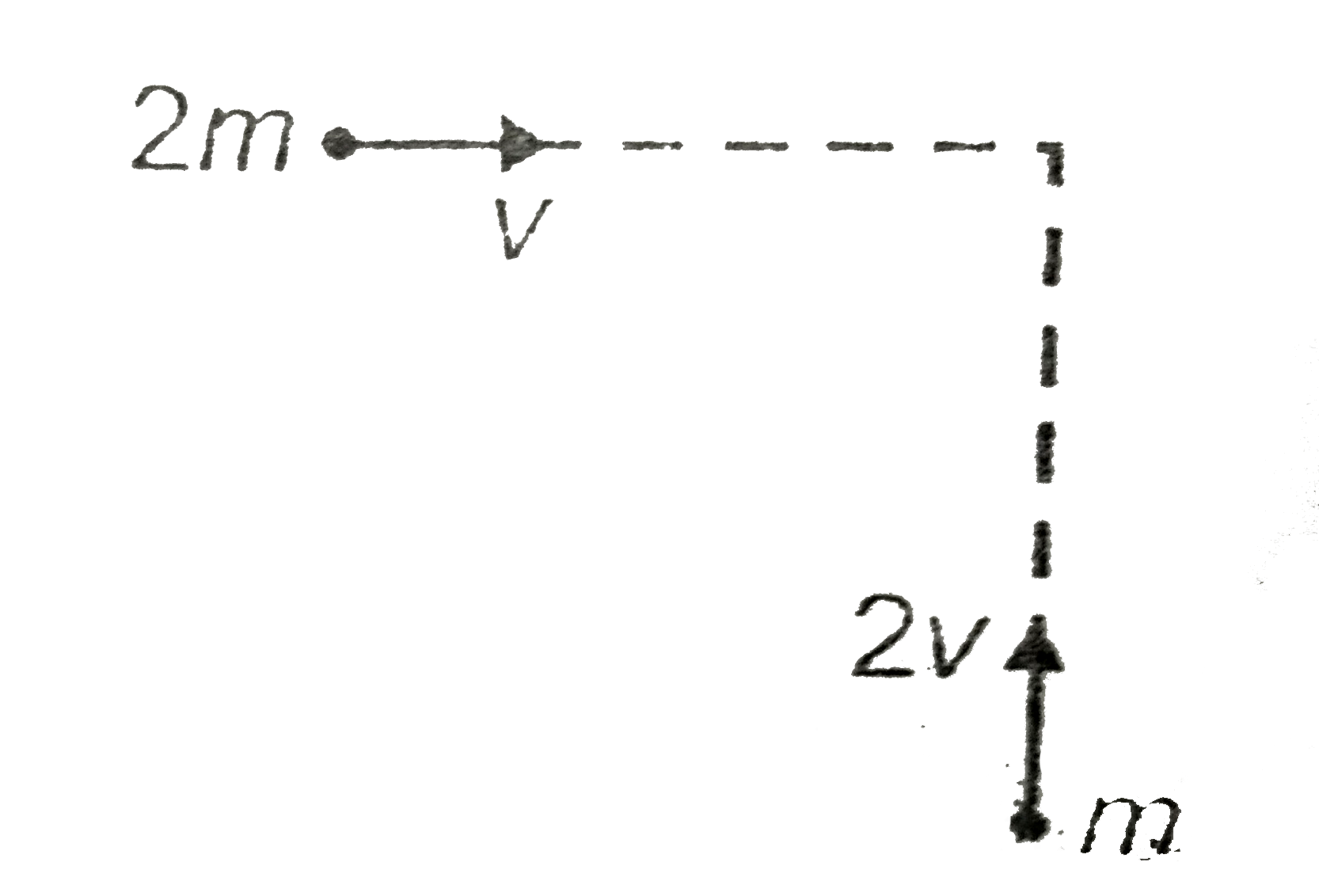
Loss in kinetic energy of the system
View SolutionA particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
View SolutionTwo ball bearings of mass m each moving in opposite directions with same speed v collide head on with each other. If the collision is perfectly elastic, what will be the outcome of the collision ?
View SolutionA and B are two identical balls. A moving with a speed of 6m/s, along the positive X-axis, undergoes a collision with B initially at rest. After collision, each ball moves along directions making angles of ±30∘ with the X-axis. What are the speeds of A and B after the collision ? I s this collision perfectly eleastic ?
View SolutionTwo particles of equal masses moving with same momentum collide perfectly in-elastically. After the collision the combined mass moves with half of the speed of the individual masses. The angle between the initial momenta of individual particle is
View Solution
